1.4空间向量与空间角(Word含答案)
文档属性
| 名称 | 1.4空间向量与空间角(Word含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 21:08:56 | ||
图片预览


文档简介
空间向量与空间角
(45分钟 100分)
一、选择题(每小题6分,共30分)
1.在空间中,已知二面角α-l-β的大小为,n1,n2分别是平面α,β的法向量,则的大小为( )
A. B. C.或 D.
2.二面角的棱上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AB=4,AC=6,BD=8,CD=2,则该二面角的大小为( )
A.150° B.45° C.60° D.120°
3.如图所示,正方体ABCD-A1B1C1D1中,M是棱DD1的中点,点O为底面ABCD的中点,P为棱A1B1上任一点,则异面直线OP与AM所成的角的大小为( )
A. B.
C. D.与点P的位置有关
4.直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=1,CB=,侧棱AA1=1,侧面AA1B1B的两条对角线交点为D,则平面B1BD与平面CBD所成角的余弦值等于( )
A.- B. C. D.-
5.在矩形ABCD中,AB=1,BC=,PA⊥平面ABCD,PA=1,则PC与平面ABCD所成角是( )
A.30° B.45° C.60° D.90°
二、填空题(每小题8分,共24分)
6.(2013·东莞高二检测)正方体ABCD-A1B1C1D1中,直线BC1与平面A1BD所成角的余弦值为 .
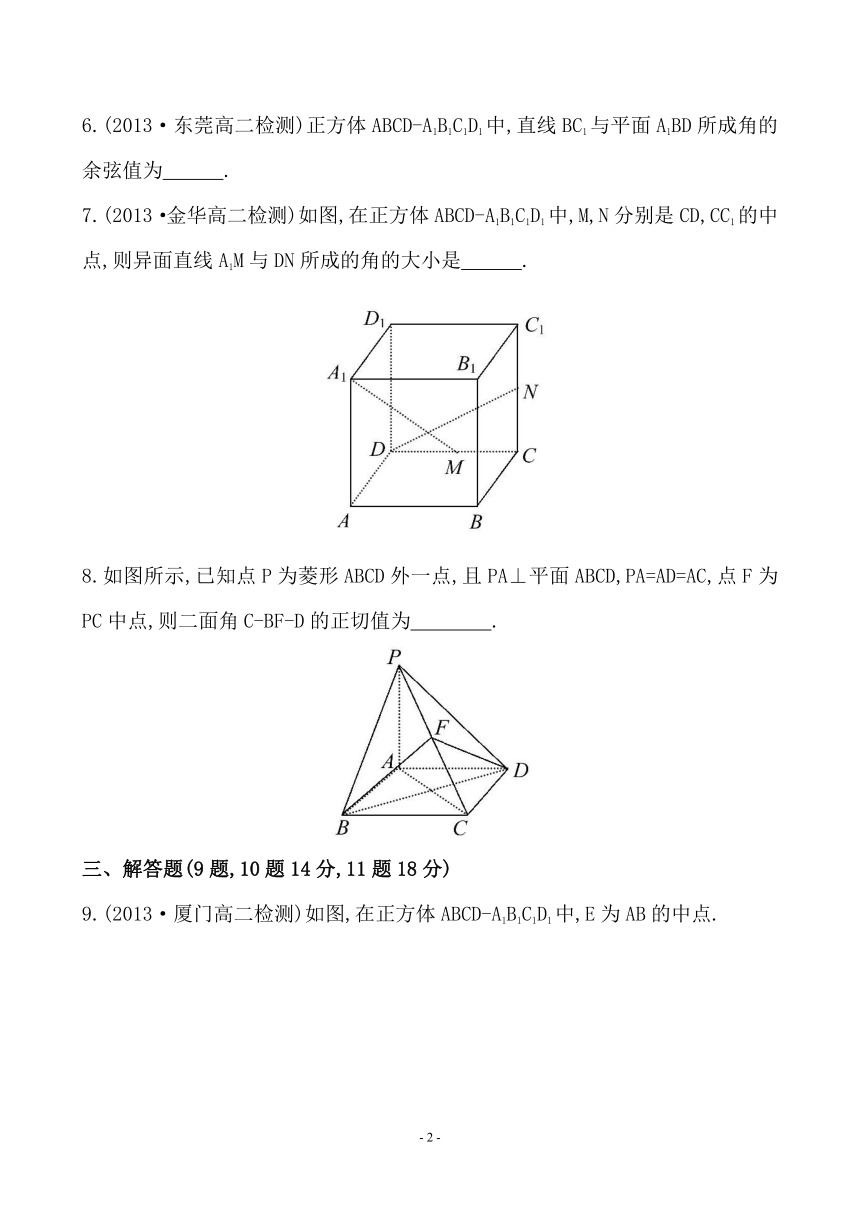
7.(2013·金华高二检测)如图,在正方体ABCD-A1B1C1D1中,M,N分别是CD,CC1的中点,则异面直线A1M与DN所成的角的大小是 .
8.如图所示,已知点P为菱形ABCD外一点,且PA⊥平面ABCD,PA=AD=AC,点F为PC中点,则二面角C-BF-D的正切值为 .
三、解答题(9题,10题14分,11题18分)
9.(2013·厦门高二检测)如图,在正方体ABCD-A1B1C1D1中,E为AB的中点.
(1)求异面直线BD1与CE所成角的余弦值.
(2)求二面角A1-EC-A的余弦值.
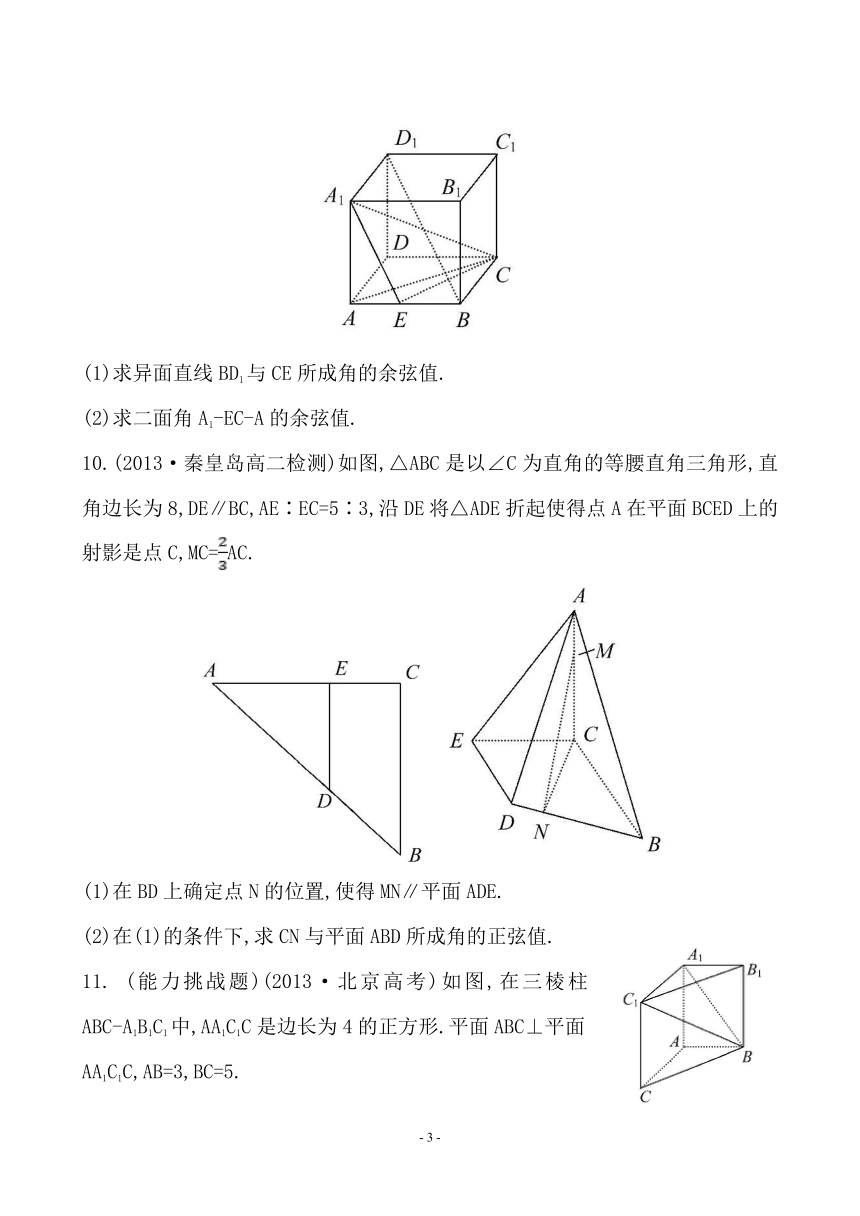
10.(2013·秦皇岛高二检测)如图,△ABC是以∠C为直角的等腰直角三角形,直角边长为8,DE∥BC,AE∶EC=5∶3,沿DE将△ADE折起使得点A在平面BCED上的射影是点C,MC=AC.
(1)在BD上确定点N的位置,使得MN∥平面ADE.
(2)在(1)的条件下,求CN与平面ABD所成角的正弦值.
11. (能力挑战题)(2013·北京高考)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
(1)求证:AA1⊥平面ABC.
(2)求二面角A1-BC1-B1的余弦值.
(3)证明:在线段BC1存在点D,使得AD⊥A1B,并求的值.
答案解析
1.【解析】选C.当为锐角时,=π-=;当为钝角时,=.故选C.
2.【解析】选C.由条件知·=0,·=0,=++,
∴||2=(++)2=62+42+82+2×6×8×cos<,>,
得cos<,>=-,∴所求二面角的大小为60°.
【变式备选】如图,在底面为直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=,则平面SCD与平面SAB所成二面角的余弦值为( )
A. B. C. D.
【解析】选B.建立如图所示的空间直角坐标系,则A(0,0,0),D(,0,0),C(1,1,0),
S(0,0,1),平面SAB的一个法向量是=(,0,0),并求得平面SCD的一个法向量n=(1,-,),cos<,n>=
=,结合图形知所求二面角的余弦值为.
3.【解题指南】本题可通过解立体几何的方法求解,或者建立空间直角坐标系用向量法来解.
【解析】选C.方法一:取AD的中点E,连接A1E,则△A1AE≌△ADM,∴∠AA1E=∠DAM,
∴∠AA1E+∠A1AM=,∴AM⊥A1E.
又PO在平面ADD1A1内的射影为A1E,
∴异面直线OP与AM所成的角的大小为.
方法二:建立如图所示的空间直角坐标系,设正方体棱长为1,则A(0,0,0),M(0,1,),O(,,0),
设P(m,0,1).
∴=(0,1,),=(m-,-,1),
∴cos<,>===0,
∴⊥,异面直线OP与AM所成的角的大小为.
4.【解析】选D.建立如图所示的坐标系,由题意可知,B(,0,0),A(0,1,0),B1(,0,1),C(0,0,0),
D(,,),
∴=(,,),=(,0,0),=(-,1,0),=
(0,0,1),设平面CBD和平面B1BD的一个法向量分别为n1,n2,求得n1=(0,1,-1),
n2=(1,,0),所以cos==,结合图形判断得平面B1BD与平面CBD所成角的余弦值为-.
5.【解析】选A.建立如图所示的空间直角坐标系,则P(0,0,1),C(1,,0),=(1,,-1),平面ABCD的一个法向量为n=(0,0,1),
所以cos<,n>==-,所以<,n>=120°,
所以斜线PC与平面ABCD的法向量所在直线所成角为60°,
所以斜线PC与平面ABCD所成角为30°.
6.【解析】如图,建立空间直角坐标系,设正方体棱长为1,则D(0,0,0),A1(1,0,1),B(1,1,0),C1(0,1,1),
∴=(1,0,1),=(1,1,0),=(-1,0,1),
设n=(x,y,z)为平面A1BD的法向量,则
∴取n=(1,-1,-1),设直线BC1与平面A1BD所成角为θ,则sinθ=|cos|= ==,
∴cosθ=.
答案:
7.【解析】如图所示,建立空间直角坐标系Dxyz,设AB=1,则A1(1,0,1),M(0,,0),N(0,1,),
∴=(-1,,-1),=(0,1,),
cos<,>===0,即⊥,则A1M与DN所成角的大小是90°.
答案:90°
8.【解析】如图所示,令AC∩BD=O,连接OF.以O为原点,OB,OC,OF所在直线分别为x,y,z轴建立空间直角坐标系.设PA=AD=AC=1,则BD=.所以B(,0,0),
F(0,0,),C(0,,0).
结合图形可知,=(0,,0)且为平面BOF的一个法向量,由=(-,,0),
=(,0,-),可求得平面BCF的一个法向量n=(1,,).
所以cos=,sin=,
所以tan=.
答案:
【误区警示】在本题中,由于空间几何体形状不是非常规则,故合理建系是关键,否则会加大运算量,并易导致失误.
9.【解析】如图所示,建立空间直角坐标系Dxyz,设AB=1,则B(1,1,0),D1(0,0,1),C(0,1,0),E(1,,0),
(1)=(-1,-1,1),=(1,-,0),故cos<,>=
==-,所以异面直线BD1与CE所成角的余弦值是.
(2)DD1⊥平面AEC,所以为平面AEC的一个法向量,=(0,0,1),设平面A1EC的法向量为n=(x,y,z),又=(0,,-1),=(-1,1,-1),
即取n=(1,2,1),
所以cos<,n>=.
结合图形知二面角A1-EC-A的余弦值为.
10.【解析】(1)由已知,点A在平面BCED上的射影是点C,则可知AC⊥平面BCED,而BC⊥CE,如图建立空间直角坐标系,则可知各点的坐标为C(0,0,0),
A(0,0,4),B(0,8,0),D(3,5,0),E(3,0,0),
由MC=AC,可知点M的坐标为(0,0,),设点N的坐标为(a,b,0),则可知b=8-a,即点N的坐标为(a,8-a,0),则=(a,8-a,-).
设平面ADE的法向量为n1=(x,y,z),由题意可知而=(0,-5,0),
=(3,0,-4),
可得取x=4,则z=3,
可得n1=(4,0,3).
要使MN∥平面ADE等价于n1·=0,即4a+0×(8-a)-3×=0,
解之可得a=2,即可知点N的坐标为(2,6,0),点N为BD的靠近D点的三等分点.
(2)由(1)可知=(2,6,0),设平面ADB的法向量为n2=(x',y',z'),由题意可知
而=(-3,3,0),=(0,8,-4)可得取x=1,则y=1,z=2,
可得n2=(1,1,2).
设CN与平面ABD所成角为θ,则sinθ==.
【拓展提升】线面角的求解策略
(1)利用直线与平面夹角的定义,找到线面角,转化为求解三角形问题.
(2)利用最小角定理,即直线与平面内任一条直线所成的角中线面角最小,代入公式cosθ=cosθ1·cosθ2求解,
(3)建立空间直角坐标系,利用直线的方向向量和平面的法向量求解.
11.【解析】(1)因为四边形AA1C1C是正方形,所以AA1⊥AC.
又因为平面ABC⊥平面AA1C1C,交线为AC,所以AA1⊥平面ABC.
(2)因为AC=4,BC=5,AB=3,所以AC⊥AB.分别以AC,AB,AA1为x轴,y轴,z轴建立如图所示的空间直角坐标系.
则A1(0,0,4),B(0,3,0),C1(4,0,4),B1(0,3,4), =(4,0,0),=(0,3,-4),=(4,-3,0),=(0,0,4).
设平面A1BC1的法向量为n1=(x1,y1,z1),平面B1BC1的法向量为n2=(x2,y2,z2),
由 可得可取n1=(0,4,3).
由 可得可取n2=(3,4,0).
所以cos= ==.
由图可知二面角A1-BC1-B1为锐角,所以余弦值为.
(3)设点D的竖轴坐标为t(0又因为⊥,所以(4-t)-4t=0,所以t=,所以==.
关闭Word文档返回原板块
PAGE
- 1 -
(45分钟 100分)
一、选择题(每小题6分,共30分)
1.在空间中,已知二面角α-l-β的大小为,n1,n2分别是平面α,β的法向量,则
A. B. C.或 D.
2.二面角的棱上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AB=4,AC=6,BD=8,CD=2,则该二面角的大小为( )
A.150° B.45° C.60° D.120°
3.如图所示,正方体ABCD-A1B1C1D1中,M是棱DD1的中点,点O为底面ABCD的中点,P为棱A1B1上任一点,则异面直线OP与AM所成的角的大小为( )
A. B.
C. D.与点P的位置有关
4.直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=1,CB=,侧棱AA1=1,侧面AA1B1B的两条对角线交点为D,则平面B1BD与平面CBD所成角的余弦值等于( )
A.- B. C. D.-
5.在矩形ABCD中,AB=1,BC=,PA⊥平面ABCD,PA=1,则PC与平面ABCD所成角是( )
A.30° B.45° C.60° D.90°
二、填空题(每小题8分,共24分)
6.(2013·东莞高二检测)正方体ABCD-A1B1C1D1中,直线BC1与平面A1BD所成角的余弦值为 .
7.(2013·金华高二检测)如图,在正方体ABCD-A1B1C1D1中,M,N分别是CD,CC1的中点,则异面直线A1M与DN所成的角的大小是 .
8.如图所示,已知点P为菱形ABCD外一点,且PA⊥平面ABCD,PA=AD=AC,点F为PC中点,则二面角C-BF-D的正切值为 .
三、解答题(9题,10题14分,11题18分)
9.(2013·厦门高二检测)如图,在正方体ABCD-A1B1C1D1中,E为AB的中点.
(1)求异面直线BD1与CE所成角的余弦值.
(2)求二面角A1-EC-A的余弦值.
10.(2013·秦皇岛高二检测)如图,△ABC是以∠C为直角的等腰直角三角形,直角边长为8,DE∥BC,AE∶EC=5∶3,沿DE将△ADE折起使得点A在平面BCED上的射影是点C,MC=AC.
(1)在BD上确定点N的位置,使得MN∥平面ADE.
(2)在(1)的条件下,求CN与平面ABD所成角的正弦值.
11. (能力挑战题)(2013·北京高考)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
(1)求证:AA1⊥平面ABC.
(2)求二面角A1-BC1-B1的余弦值.
(3)证明:在线段BC1存在点D,使得AD⊥A1B,并求的值.
答案解析
1.【解析】选C.当
2.【解析】选C.由条件知·=0,·=0,=++,
∴||2=(++)2=62+42+82+2×6×8×cos<,>,
得cos<,>=-,∴所求二面角的大小为60°.
【变式备选】如图,在底面为直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=,则平面SCD与平面SAB所成二面角的余弦值为( )
A. B. C. D.
【解析】选B.建立如图所示的空间直角坐标系,则A(0,0,0),D(,0,0),C(1,1,0),
S(0,0,1),平面SAB的一个法向量是=(,0,0),并求得平面SCD的一个法向量n=(1,-,),cos<,n>=
=,结合图形知所求二面角的余弦值为.
3.【解题指南】本题可通过解立体几何的方法求解,或者建立空间直角坐标系用向量法来解.
【解析】选C.方法一:取AD的中点E,连接A1E,则△A1AE≌△ADM,∴∠AA1E=∠DAM,
∴∠AA1E+∠A1AM=,∴AM⊥A1E.
又PO在平面ADD1A1内的射影为A1E,
∴异面直线OP与AM所成的角的大小为.
方法二:建立如图所示的空间直角坐标系,设正方体棱长为1,则A(0,0,0),M(0,1,),O(,,0),
设P(m,0,1).
∴=(0,1,),=(m-,-,1),
∴cos<,>===0,
∴⊥,异面直线OP与AM所成的角的大小为.
4.【解析】选D.建立如图所示的坐标系,由题意可知,B(,0,0),A(0,1,0),B1(,0,1),C(0,0,0),
D(,,),
∴=(,,),=(,0,0),=(-,1,0),=
(0,0,1),设平面CBD和平面B1BD的一个法向量分别为n1,n2,求得n1=(0,1,-1),
n2=(1,,0),所以cos
5.【解析】选A.建立如图所示的空间直角坐标系,则P(0,0,1),C(1,,0),=(1,,-1),平面ABCD的一个法向量为n=(0,0,1),
所以cos<,n>==-,所以<,n>=120°,
所以斜线PC与平面ABCD的法向量所在直线所成角为60°,
所以斜线PC与平面ABCD所成角为30°.
6.【解析】如图,建立空间直角坐标系,设正方体棱长为1,则D(0,0,0),A1(1,0,1),B(1,1,0),C1(0,1,1),
∴=(1,0,1),=(1,1,0),=(-1,0,1),
设n=(x,y,z)为平面A1BD的法向量,则
∴取n=(1,-1,-1),设直线BC1与平面A1BD所成角为θ,则sinθ=|cos
∴cosθ=.
答案:
7.【解析】如图所示,建立空间直角坐标系Dxyz,设AB=1,则A1(1,0,1),M(0,,0),N(0,1,),
∴=(-1,,-1),=(0,1,),
cos<,>===0,即⊥,则A1M与DN所成角的大小是90°.
答案:90°
8.【解析】如图所示,令AC∩BD=O,连接OF.以O为原点,OB,OC,OF所在直线分别为x,y,z轴建立空间直角坐标系.设PA=AD=AC=1,则BD=.所以B(,0,0),
F(0,0,),C(0,,0).
结合图形可知,=(0,,0)且为平面BOF的一个法向量,由=(-,,0),
=(,0,-),可求得平面BCF的一个法向量n=(1,,).
所以cos
所以tan
答案:
【误区警示】在本题中,由于空间几何体形状不是非常规则,故合理建系是关键,否则会加大运算量,并易导致失误.
9.【解析】如图所示,建立空间直角坐标系Dxyz,设AB=1,则B(1,1,0),D1(0,0,1),C(0,1,0),E(1,,0),
(1)=(-1,-1,1),=(1,-,0),故cos<,>=
==-,所以异面直线BD1与CE所成角的余弦值是.
(2)DD1⊥平面AEC,所以为平面AEC的一个法向量,=(0,0,1),设平面A1EC的法向量为n=(x,y,z),又=(0,,-1),=(-1,1,-1),
即取n=(1,2,1),
所以cos<,n>=.
结合图形知二面角A1-EC-A的余弦值为.
10.【解析】(1)由已知,点A在平面BCED上的射影是点C,则可知AC⊥平面BCED,而BC⊥CE,如图建立空间直角坐标系,则可知各点的坐标为C(0,0,0),
A(0,0,4),B(0,8,0),D(3,5,0),E(3,0,0),
由MC=AC,可知点M的坐标为(0,0,),设点N的坐标为(a,b,0),则可知b=8-a,即点N的坐标为(a,8-a,0),则=(a,8-a,-).
设平面ADE的法向量为n1=(x,y,z),由题意可知而=(0,-5,0),
=(3,0,-4),
可得取x=4,则z=3,
可得n1=(4,0,3).
要使MN∥平面ADE等价于n1·=0,即4a+0×(8-a)-3×=0,
解之可得a=2,即可知点N的坐标为(2,6,0),点N为BD的靠近D点的三等分点.
(2)由(1)可知=(2,6,0),设平面ADB的法向量为n2=(x',y',z'),由题意可知
而=(-3,3,0),=(0,8,-4)可得取x=1,则y=1,z=2,
可得n2=(1,1,2).
设CN与平面ABD所成角为θ,则sinθ==.
【拓展提升】线面角的求解策略
(1)利用直线与平面夹角的定义,找到线面角,转化为求解三角形问题.
(2)利用最小角定理,即直线与平面内任一条直线所成的角中线面角最小,代入公式cosθ=cosθ1·cosθ2求解,
(3)建立空间直角坐标系,利用直线的方向向量和平面的法向量求解.
11.【解析】(1)因为四边形AA1C1C是正方形,所以AA1⊥AC.
又因为平面ABC⊥平面AA1C1C,交线为AC,所以AA1⊥平面ABC.
(2)因为AC=4,BC=5,AB=3,所以AC⊥AB.分别以AC,AB,AA1为x轴,y轴,z轴建立如图所示的空间直角坐标系.
则A1(0,0,4),B(0,3,0),C1(4,0,4),B1(0,3,4), =(4,0,0),=(0,3,-4),=(4,-3,0),=(0,0,4).
设平面A1BC1的法向量为n1=(x1,y1,z1),平面B1BC1的法向量为n2=(x2,y2,z2),
由 可得可取n1=(0,4,3).
由 可得可取n2=(3,4,0).
所以cos
由图可知二面角A1-BC1-B1为锐角,所以余弦值为.
(3)设点D的竖轴坐标为t(0
关闭Word文档返回原板块
PAGE
- 1 -
