人教版五年级下学期数学 探索图形 课件(16张PPT)
文档属性
| 名称 | 人教版五年级下学期数学 探索图形 课件(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 32.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
探索图形
五年级下册
人教版
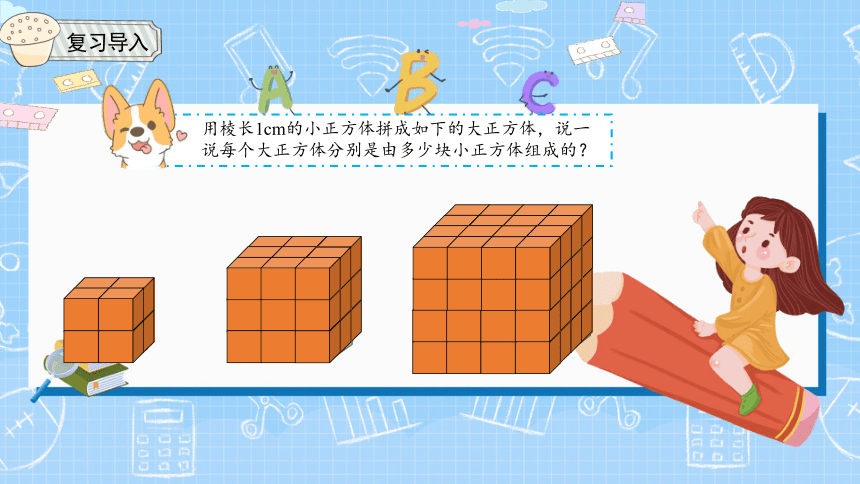
用棱长1cm的小正方体拼成如下的大正方体,说一说每个大正方体分别是由多少块小正方体组成的?
复习导入
探索规律
2面涂色的小正方体有多少个?
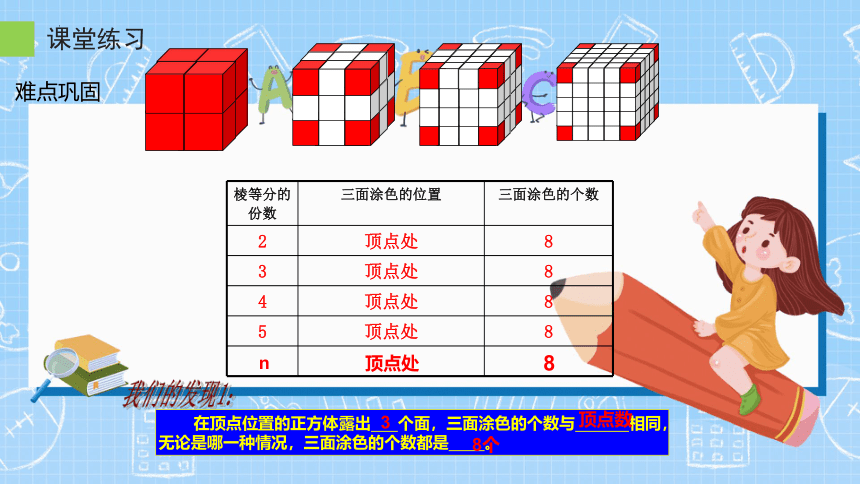
棱等分的份数 三面涂色的位置 三面涂色的个数
2 顶点处 8
3 顶点处 8
4 顶点处 8
5 顶点处 8
在顶点位置的正方体露出 个面,三面涂色的个数与 相同,无论是哪一种情况,三面涂色的个数都是 。
顶点处
8
n
3
顶点数
8个
课堂练习
难点巩固
观察上表,你还能发现什么?
在每条棱中间位置的正方体露出2个面,两面涂色的块数与棱有关,即(n-2)×12。
新课讲解
摆成下面的几何体,各需要多少个小正方体?
课堂练习
4
10
20
3面涂色
顶点
2面涂色
棱的中间
1面涂色
面的中间
0面涂色
里面
想一想,它们各在什么位置?
探索规律3
1面涂色的小正方体有多少个?
课堂游戏
免作业一次
零食一份
拆红包啦
+5分
每条棱被平均分成n份
每个面有 个
1面涂色的小正方体。
(n-2)
2
6个面有 个
1面涂色的小正方体。
×6
(n-2)
2
…
一面涂色的个数规律
拓展延伸
① ② ③
棱平均分的份数 2 3 4 5 6
3面涂色的个数 8 8 8
2面涂色的个数 0 12 24
1面涂色的个数 0 6 24
0面涂色的个数 0 1 8
①
②
③
课后思考
课堂小结
在顶点位置的正方体露出3个面,三面涂色的块数与顶点数相同,无论是哪一种正方体都是8个。
在每条棱中间位置的正方体露出2个面,两面涂色的块数与棱有关,即(n-2)×12。
在每个面中间位置的正方体露出1个面,一面涂色的块数与面有关,即(n-2)×(n-2)×6。
同学们再见
探索图形
五年级下册
人教版
用棱长1cm的小正方体拼成如下的大正方体,说一说每个大正方体分别是由多少块小正方体组成的?
复习导入
探索规律
2面涂色的小正方体有多少个?
棱等分的份数 三面涂色的位置 三面涂色的个数
2 顶点处 8
3 顶点处 8
4 顶点处 8
5 顶点处 8
在顶点位置的正方体露出 个面,三面涂色的个数与 相同,无论是哪一种情况,三面涂色的个数都是 。
顶点处
8
n
3
顶点数
8个
课堂练习
难点巩固
观察上表,你还能发现什么?
在每条棱中间位置的正方体露出2个面,两面涂色的块数与棱有关,即(n-2)×12。
新课讲解
摆成下面的几何体,各需要多少个小正方体?
课堂练习
4
10
20
3面涂色
顶点
2面涂色
棱的中间
1面涂色
面的中间
0面涂色
里面
想一想,它们各在什么位置?
探索规律3
1面涂色的小正方体有多少个?
课堂游戏
免作业一次
零食一份
拆红包啦
+5分
每条棱被平均分成n份
每个面有 个
1面涂色的小正方体。
(n-2)
2
6个面有 个
1面涂色的小正方体。
×6
(n-2)
2
…
一面涂色的个数规律
拓展延伸
① ② ③
棱平均分的份数 2 3 4 5 6
3面涂色的个数 8 8 8
2面涂色的个数 0 12 24
1面涂色的个数 0 6 24
0面涂色的个数 0 1 8
①
②
③
课后思考
课堂小结
在顶点位置的正方体露出3个面,三面涂色的块数与顶点数相同,无论是哪一种正方体都是8个。
在每条棱中间位置的正方体露出2个面,两面涂色的块数与棱有关,即(n-2)×12。
在每个面中间位置的正方体露出1个面,一面涂色的块数与面有关,即(n-2)×(n-2)×6。
同学们再见
