人教版五年级下学期数学 总复习 课件(20张PPT)
文档属性
| 名称 | 人教版五年级下学期数学 总复习 课件(20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
总复习
1、我能理清因数和倍数的相关知识。
2、我能熟练地掌握因数与倍数、质数与合数等重要的概念。
3、我能熟练地掌握求因数、倍数的方法。
4、培养学生分析问题能力和语言表达能力,感受数学与实际生活的联系。
一、复习目标
长方体和正方体的特征
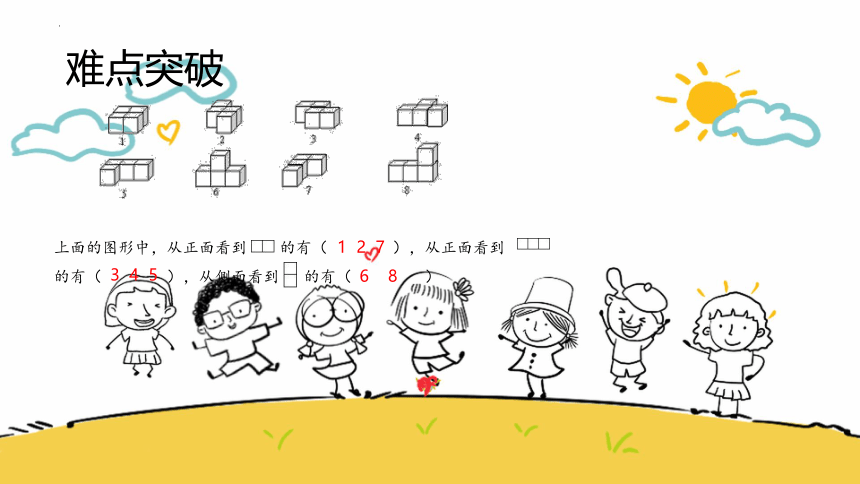
难点突破
上面的图形中,从正面看到 的有( ),从正面看到 的有( ),从侧面看到 的有( )
1 2 7
3 4 5
6 8
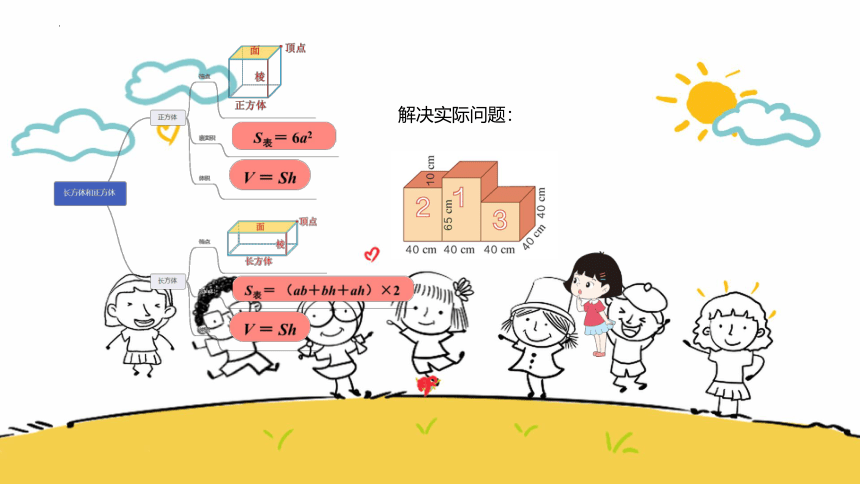
解决实际问题:
知识梳理
在打电话通知同学的活动中你发现了什么?
如果采用最优打电话方案,那么通知的人数是以翻倍的方式递增的。过了几分钟,通知到的人数就是几个2相乘再减1。
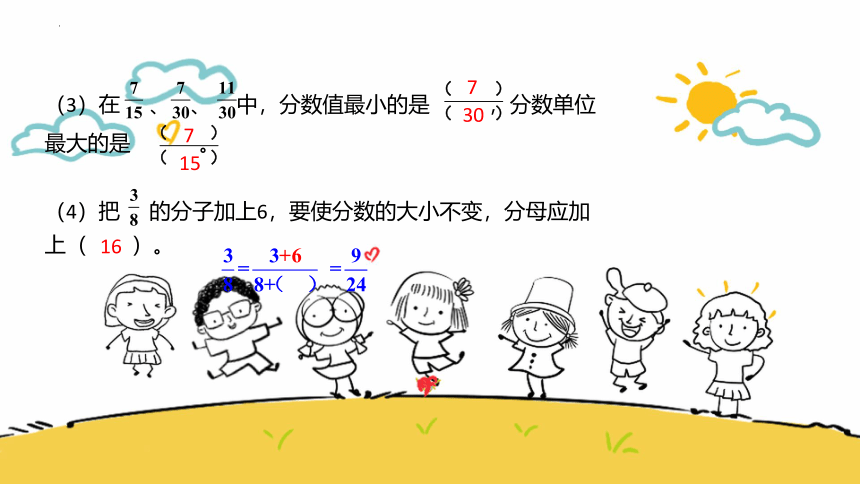
(3)在 、 、 中,分数值最小的是 ,分数单位最大的是 。
(4)把 的分子加上6,要使分数的大小不变,分母应加上( )。
7
30
7
15
16
知识梳理
我们一起来回忆:怎么绘制折线统计图呢?折线统计图时要注意什么?
先写标题,画横轴、纵轴,写图例等与条形统计图相同。
根据数据在横轴、纵轴的交点处描点,再标数据;最后用直线把点与点连接起来。
一个工厂中甲车间有42人,乙车间有48人。把两个车间的工人分成人数相等的小组,每组最多有多少人 这时每个车间分别有几组?[★★★]
42和48的最大公因数是6。
42÷6=7(组) 48÷6=8(组)
答:每组最多有6人,这时甲车间有7组,乙车间有8组。
42 48
2
21 24
3
7 8
(42,48)=2×3=6
随堂检测
2.阿米巴原虫(一种主要寄生于结肠内的虫,会引起阿米巴痢疾或阿米巴结肠炎)是用简单分裂的方式繁殖的,每分裂一次要用3分钟。请问一个阿米巴原虫18分钟后变成了几个阿米巴原虫?
18÷3=6(次)
2×2×2×2×2×2=64(个)
一个阿米巴原虫18分钟后变成64个阿米巴原虫。
1、20以内的偶数有( ),奇数( )。
2、是2的倍数的最小的两位数是( ),最大的三位数是( )。
3、有因数5的最小的三位数是( )最大的两位数是( )。
4、同时有因数2和5的数的个位必须是( )。
5、有因数3的最小的两位数是( ),最大两位数是( ),最小三位数( ),最大的三位数( )。
学习提示:先独立完成,后小组交流,全班展示。
当堂检测
随堂检测
.5瓶钙片中有1瓶是次品(轻一些),完成下面找次品的过程。
至少要称____次。
5
2
1
2
平衡。
不平衡,轻的是次品。
3
4
平衡,次品是 。
不平衡,轻的是次品。
随堂检测
4. 有15盒饼干,其中的14盒质量相同,另有1盒少了几块。如果能用天平称,至少称几次可以保证找出这盒饼干?
平衡:(2次)
平衡:5(2,2,1)2,2
不平衡:2(1,1)(3次)
15(5,5,5)5,5
平衡:(2次)
不平衡:5(2,2,1)2,2
不平衡:2(1,1)(3次)
随堂检测
、(1)观察这两个折线统计图所表示的数据,说一说折线统计图适合表示数据的什么情况。
(2)说一说绘制复式折线统计图时应注意什么?
(3)如果你是高考生或者商场经理,你能从统计图中得到哪些信息?这些信息对你有什么帮助?
(2)2017年A市第一季度人均食品支出占人均支出的 。
(3)2021年A市第一季度人均食品支出占人均支出的 。
4
5
8
21
探索图形
三面涂色:块数与顶点数相同,无论是哪一种正方体都是8个。
两面涂色:两面涂色的块数与棱有关,即(n-2)×12。
没有涂色的:正方体每个面剥离后剩下的小正方体,小正方体的块数就是小正方体的体积,即(n-2)3。
一面涂色:一面涂色的块数与面有关,即(n-2)×(n-2)×6。
把待测的物品数量平均分成3份,不能平均分的尽量平均分,保证有两份数量相同,并只比另一份多1或少1,这是最优的方法。
如果采用最优打电话方案,那么通知的人数是以翻倍的方式递增的。过了几分钟,通知到的人数就是几个2相乘再减1.
打电话
找次品
综合实践
小结:
求因数、倍数的方法:
(1)求因数的方法:先写出这个整数作被除数的所有整数除法中能整除且商是整数的除法算式,看除数有哪些数,这些不同的除数就是这个数的因数。
(2)求倍数的方法:这个整数分别与从1开始的整数相乘的所有积,都是这个数的倍数。
说明:一个数的因数的个数是有限的,最小是1,最大是它本身,一个数的倍数的个数是无限的,最小是它本身,没有最大倍数。
课后作业
完成9.3总复习(3)课后作业
聪明出于勤奋,天才在于积累。
总复习
1、我能理清因数和倍数的相关知识。
2、我能熟练地掌握因数与倍数、质数与合数等重要的概念。
3、我能熟练地掌握求因数、倍数的方法。
4、培养学生分析问题能力和语言表达能力,感受数学与实际生活的联系。
一、复习目标
长方体和正方体的特征
难点突破
上面的图形中,从正面看到 的有( ),从正面看到 的有( ),从侧面看到 的有( )
1 2 7
3 4 5
6 8
解决实际问题:
知识梳理
在打电话通知同学的活动中你发现了什么?
如果采用最优打电话方案,那么通知的人数是以翻倍的方式递增的。过了几分钟,通知到的人数就是几个2相乘再减1。
(3)在 、 、 中,分数值最小的是 ,分数单位最大的是 。
(4)把 的分子加上6,要使分数的大小不变,分母应加上( )。
7
30
7
15
16
知识梳理
我们一起来回忆:怎么绘制折线统计图呢?折线统计图时要注意什么?
先写标题,画横轴、纵轴,写图例等与条形统计图相同。
根据数据在横轴、纵轴的交点处描点,再标数据;最后用直线把点与点连接起来。
一个工厂中甲车间有42人,乙车间有48人。把两个车间的工人分成人数相等的小组,每组最多有多少人 这时每个车间分别有几组?[★★★]
42和48的最大公因数是6。
42÷6=7(组) 48÷6=8(组)
答:每组最多有6人,这时甲车间有7组,乙车间有8组。
42 48
2
21 24
3
7 8
(42,48)=2×3=6
随堂检测
2.阿米巴原虫(一种主要寄生于结肠内的虫,会引起阿米巴痢疾或阿米巴结肠炎)是用简单分裂的方式繁殖的,每分裂一次要用3分钟。请问一个阿米巴原虫18分钟后变成了几个阿米巴原虫?
18÷3=6(次)
2×2×2×2×2×2=64(个)
一个阿米巴原虫18分钟后变成64个阿米巴原虫。
1、20以内的偶数有( ),奇数( )。
2、是2的倍数的最小的两位数是( ),最大的三位数是( )。
3、有因数5的最小的三位数是( )最大的两位数是( )。
4、同时有因数2和5的数的个位必须是( )。
5、有因数3的最小的两位数是( ),最大两位数是( ),最小三位数( ),最大的三位数( )。
学习提示:先独立完成,后小组交流,全班展示。
当堂检测
随堂检测
.5瓶钙片中有1瓶是次品(轻一些),完成下面找次品的过程。
至少要称____次。
5
2
1
2
平衡。
不平衡,轻的是次品。
3
4
平衡,次品是 。
不平衡,轻的是次品。
随堂检测
4. 有15盒饼干,其中的14盒质量相同,另有1盒少了几块。如果能用天平称,至少称几次可以保证找出这盒饼干?
平衡:(2次)
平衡:5(2,2,1)2,2
不平衡:2(1,1)(3次)
15(5,5,5)5,5
平衡:(2次)
不平衡:5(2,2,1)2,2
不平衡:2(1,1)(3次)
随堂检测
、(1)观察这两个折线统计图所表示的数据,说一说折线统计图适合表示数据的什么情况。
(2)说一说绘制复式折线统计图时应注意什么?
(3)如果你是高考生或者商场经理,你能从统计图中得到哪些信息?这些信息对你有什么帮助?
(2)2017年A市第一季度人均食品支出占人均支出的 。
(3)2021年A市第一季度人均食品支出占人均支出的 。
4
5
8
21
探索图形
三面涂色:块数与顶点数相同,无论是哪一种正方体都是8个。
两面涂色:两面涂色的块数与棱有关,即(n-2)×12。
没有涂色的:正方体每个面剥离后剩下的小正方体,小正方体的块数就是小正方体的体积,即(n-2)3。
一面涂色:一面涂色的块数与面有关,即(n-2)×(n-2)×6。
把待测的物品数量平均分成3份,不能平均分的尽量平均分,保证有两份数量相同,并只比另一份多1或少1,这是最优的方法。
如果采用最优打电话方案,那么通知的人数是以翻倍的方式递增的。过了几分钟,通知到的人数就是几个2相乘再减1.
打电话
找次品
综合实践
小结:
求因数、倍数的方法:
(1)求因数的方法:先写出这个整数作被除数的所有整数除法中能整除且商是整数的除法算式,看除数有哪些数,这些不同的除数就是这个数的因数。
(2)求倍数的方法:这个整数分别与从1开始的整数相乘的所有积,都是这个数的倍数。
说明:一个数的因数的个数是有限的,最小是1,最大是它本身,一个数的倍数的个数是无限的,最小是它本身,没有最大倍数。
课后作业
完成9.3总复习(3)课后作业
聪明出于勤奋,天才在于积累。
