人教版五年级下学期数学第四单元4.6分数和小数的互化 课件 (共20张PPT)
文档属性
| 名称 | 人教版五年级下学期数学第四单元4.6分数和小数的互化 课件 (共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 22.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
分数和小数的互化
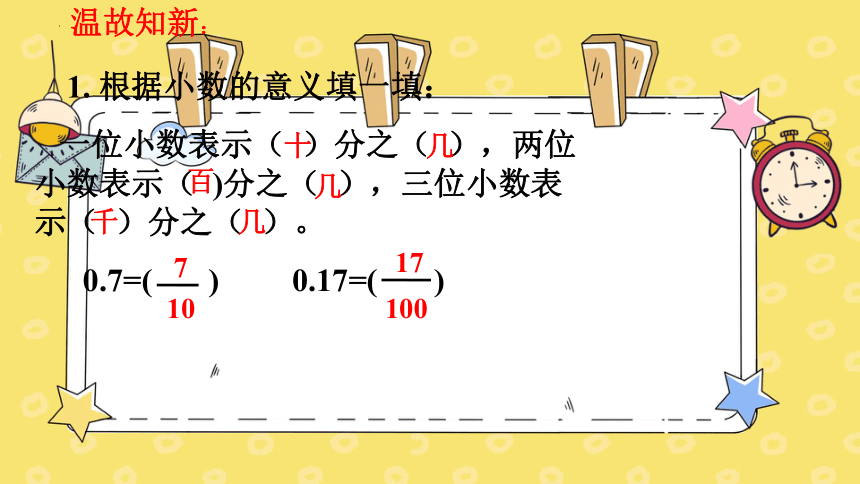
温故知新:
1. 根据小数的意义填一填:
一位小数表示( )分之( ),两位小数表示( )分之( ),三位小数表示( )分之( )。
0.7=( ) 0.17=( )
几
几
十
千
几
百
100
17
10
7
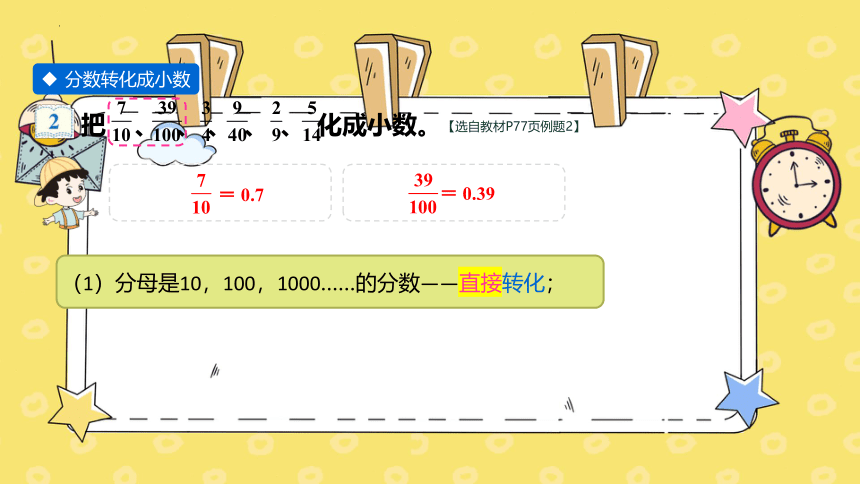
把 、 、 、 、 、 化成小数。
分数转化成小数
(1)分母是10,100,1000……的分数——直接转化;
【选自教材P77页例题2】
3÷5=0.6(m)
3÷5= (m)
如果把一条3m长的绳子平均分成5段,每段长多少米?
5
3
3
5
需要化简的分数,要化简成最简分数。
小数化成分数,需要注意什么?
自己试一试
0.07=
7
( )
=
( )
( )
0.24=
24
( )
0.123=
( )
( )
100
100
25
6
1000
123
新知讲解
10
3
= (m)
=0.3(m)
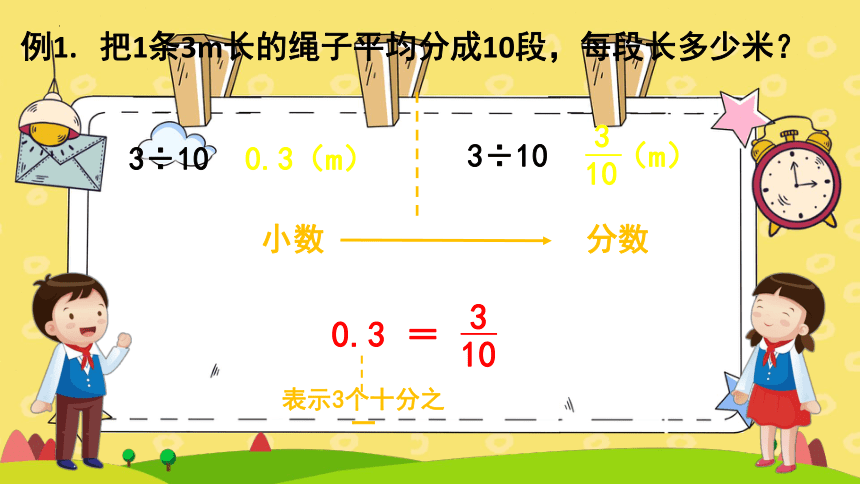
例1. 把1条3m长的绳子平均分成10段,每段长多少米?
3÷10
小数
分数
0.3(m)
10
3
(m)
0.3
=
10
3
表示3个十分之一
3÷10
新课讲解
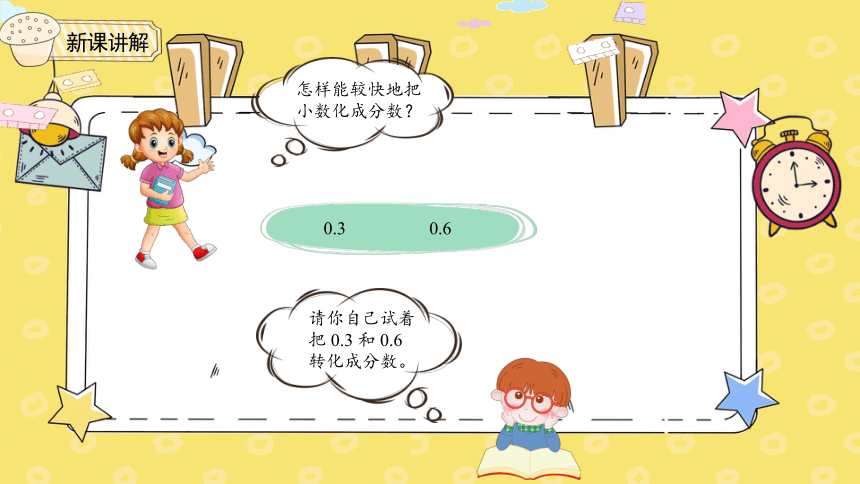
怎样能较快地把小数化成分数?
0.3
0.6
请你自己试着把 0.3 和 0.6 转化成分数。
例 :把下列分数化成小数。
9
40
2
9
5
14
3
4
39
100
7
10
(除不尽的保留两位小数)
结合以上分数特点思考交流:
怎样把分数化成小数? (尽量要全面简洁)
小数转化成分数
0.225
=
分母是几个0就是几位小数,所以我根据小数的位数直接把小数转化成分母是10、100、1000······的分数,然后再约分化简。
225
1000
=
9
40
(1)、上衣的价格是裤子的几倍?
85÷50=1.7
答:上衣的价格是裤子的1.7倍。
(2)、裤子的价格是上衣的几分之几?
50÷85=
答:裤子的价格是上衣的 。
课堂练习
例2: 把 、 、 、 、 、 化成小数
(除不尽的保留两位小数)。
10
7
100
39
4
3
40
9
14
5
9
2
=
0.7
10
7
=
0.39
100
39
=3÷4
4
3
40
9
=0.75
=9÷40
=0.225
①利用分数和除法的关系。
4
3
=0.75
4×25
3×25
=
100
75
=
40
9
=0.225
40×25
9×25
=
1000
225
=
②将该分数转化成分母是10、100、1000、…的分数,再转化成小数。
用分子除以分母除不尽时,要根据需要按“四舍五入”法保留几位小数。
新课讲解
怎样能较快地把分数化成小数?
把 、 、 、 、 、 化成小数(不能化成有限小数的保留两位有效小数)。
10
7
100
39
4
3
40
9
14
5
9
2
新课讲解
=0.7
10
7
4
3
9
2
=0.39
100
39
40
9
14
5
=3÷4=0.75
=2÷9≈0.22
=9÷40=0.225
=5÷14≈0.36
说说你的想法。
这样转化的依据是什么?
把小数化成分数要注意什么?
新课讲解
用分子除以分母除不尽时,要根据需要按“四舍五入”法保留几位小数。
新课讲解
把0.a化成分数,不要约分就是一个最简分数,这样的小数有多少个?
动脑筋:
在学校竞走比赛中,状状用 小时走完全程,元元用 小时走完全程,路路用0.67小时走完全程。谁应获得冠军 [★★★★]
答:元元应获得冠军。
探究课本第79页:
“你知道吗?”
什么样的最简分数能化成有限小数?
方法一:0.9 ×60=54(个) 54 > 50
方法二: =5÷6≈0.83(个) 0.9 >0.83
6
5
知识运用
感谢同学们积极配合!
分数和小数的互化
温故知新:
1. 根据小数的意义填一填:
一位小数表示( )分之( ),两位小数表示( )分之( ),三位小数表示( )分之( )。
0.7=( ) 0.17=( )
几
几
十
千
几
百
100
17
10
7
把 、 、 、 、 、 化成小数。
分数转化成小数
(1)分母是10,100,1000……的分数——直接转化;
【选自教材P77页例题2】
3÷5=0.6(m)
3÷5= (m)
如果把一条3m长的绳子平均分成5段,每段长多少米?
5
3
3
5
需要化简的分数,要化简成最简分数。
小数化成分数,需要注意什么?
自己试一试
0.07=
7
( )
=
( )
( )
0.24=
24
( )
0.123=
( )
( )
100
100
25
6
1000
123
新知讲解
10
3
= (m)
=0.3(m)
例1. 把1条3m长的绳子平均分成10段,每段长多少米?
3÷10
小数
分数
0.3(m)
10
3
(m)
0.3
=
10
3
表示3个十分之一
3÷10
新课讲解
怎样能较快地把小数化成分数?
0.3
0.6
请你自己试着把 0.3 和 0.6 转化成分数。
例 :把下列分数化成小数。
9
40
2
9
5
14
3
4
39
100
7
10
(除不尽的保留两位小数)
结合以上分数特点思考交流:
怎样把分数化成小数? (尽量要全面简洁)
小数转化成分数
0.225
=
分母是几个0就是几位小数,所以我根据小数的位数直接把小数转化成分母是10、100、1000······的分数,然后再约分化简。
225
1000
=
9
40
(1)、上衣的价格是裤子的几倍?
85÷50=1.7
答:上衣的价格是裤子的1.7倍。
(2)、裤子的价格是上衣的几分之几?
50÷85=
答:裤子的价格是上衣的 。
课堂练习
例2: 把 、 、 、 、 、 化成小数
(除不尽的保留两位小数)。
10
7
100
39
4
3
40
9
14
5
9
2
=
0.7
10
7
=
0.39
100
39
=3÷4
4
3
40
9
=0.75
=9÷40
=0.225
①利用分数和除法的关系。
4
3
=0.75
4×25
3×25
=
100
75
=
40
9
=0.225
40×25
9×25
=
1000
225
=
②将该分数转化成分母是10、100、1000、…的分数,再转化成小数。
用分子除以分母除不尽时,要根据需要按“四舍五入”法保留几位小数。
新课讲解
怎样能较快地把分数化成小数?
把 、 、 、 、 、 化成小数(不能化成有限小数的保留两位有效小数)。
10
7
100
39
4
3
40
9
14
5
9
2
新课讲解
=0.7
10
7
4
3
9
2
=0.39
100
39
40
9
14
5
=3÷4=0.75
=2÷9≈0.22
=9÷40=0.225
=5÷14≈0.36
说说你的想法。
这样转化的依据是什么?
把小数化成分数要注意什么?
新课讲解
用分子除以分母除不尽时,要根据需要按“四舍五入”法保留几位小数。
新课讲解
把0.a化成分数,不要约分就是一个最简分数,这样的小数有多少个?
动脑筋:
在学校竞走比赛中,状状用 小时走完全程,元元用 小时走完全程,路路用0.67小时走完全程。谁应获得冠军 [★★★★]
答:元元应获得冠军。
探究课本第79页:
“你知道吗?”
什么样的最简分数能化成有限小数?
方法一:0.9 ×60=54(个) 54 > 50
方法二: =5÷6≈0.83(个) 0.9 >0.83
6
5
知识运用
感谢同学们积极配合!
