1.3 动量守恒定律(共27张ppt)
文档属性
| 名称 | 1.3 动量守恒定律(共27张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-05-20 12:53:35 | ||
图片预览







文档简介
(共27张PPT)
第一章 动量守恒定律
1.3.1 动量守恒定律
F·Δt= mv' – mv0=Δp
单个物体动量变化的原因是合外力的冲量所致
相互碰撞的两物体动量都发生变化,但动量的总量保持不变
温故知新
动量的总量为什么会保持不变?
动量守恒要满足什么条件吗?
为什么会都发生变化?
注意:内力和外力的区分依赖于系统的选取,只有在确定了系统后,才能确定内力和外力。
系统:我们把两个(或多个)相互作用的物体构成的整体叫做一个力学系统。系统可按解决问题的需要灵活选取。
内力:系统中物体间的相互作用力叫做内力。
外力:系统以外的物体施加给系统内任何一个物体的力,叫做外力。
一、基本概念
选ABC为系统:A与C、B与C之间的摩擦力为内力还是外力?
选AB为系统:A与C、B与C之间的摩擦力为内力还是外力?
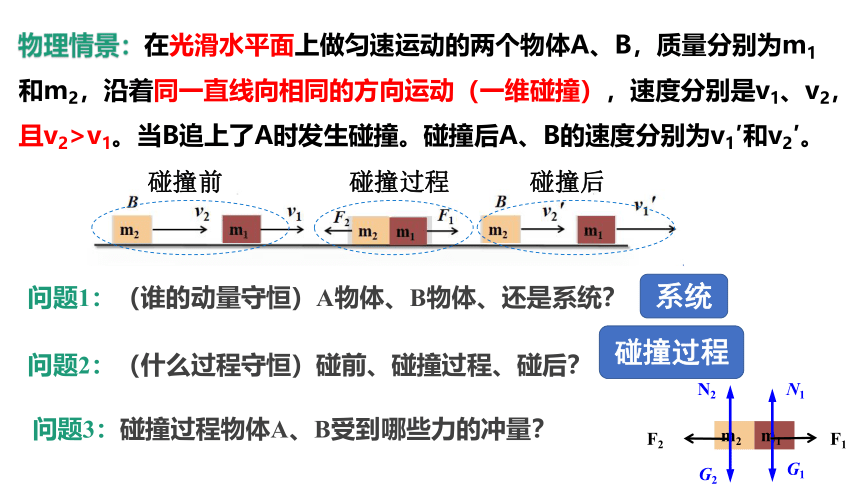
物理情景:在光滑水平面上做匀速运动的两个物体A、B,质量分别为m1和m2,沿着同一直线向相同的方向运动(一维碰撞),速度分别是v1、v2,且v2>v1。当B追上了A时发生碰撞。碰撞后A、B的速度分别为v1′和v2′。
碰撞过程
碰撞前
碰撞后
问题1:(谁的动量守恒)A物体、B物体、还是系统?
系统
问题2:(什么过程守恒)碰前、碰撞过程、碰后?
碰撞过程
问题3:碰撞过程物体A、B受到哪些力的冲量?
m2
m1
G1
N1
N2
G2
F2
F1
B
v2
m2
A
v1
m1
B
v2'
m2
A
v1'
m1
碰撞过程
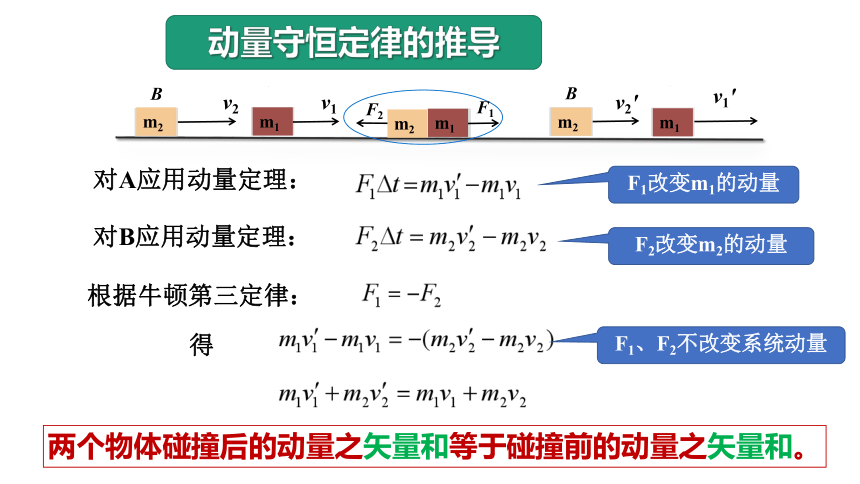
对A应用动量定理:
对B应用动量定理:
根据牛顿第三定律:
得
两个物体碰撞后的动量之矢量和等于碰撞前的动量之矢量和。
F1
F2
m2
m1
动量守恒定律的推导
F1改变m1的动量
F2改变m2的动量
F1、F2不改变系统动量
碰撞过程
两个碰撞物体外部作用力的矢量和为0的情况下动量守恒。
思考:A、B系统,哪些力是内力?内力作用效果如何?
外力矢量和为零时,外力冲量为零,系统动量不变
守恒条件分析
思考:A、B系统,哪些力是外力?作用效果如何?外力的矢量和是多少?
内力只改变单个物体动量,不改变系统总动量。
外力既改变单个物体动量,也改变系统总动量。
m2
m1
G1
N1
N2
G2
F2
F1
如果一个系统不受外力,或者所受外力的矢量和为0,
这个系统的总动量保持不变。这就是动量守恒定律。
1.内容:
2.表达式:
(3)Δp=0
(1)p=p′或m1v1+m2v2=m1v1′+m2v2′
(2)Δp1=-Δp2 或 m1Δv1=-m2Δv2
(系统作用前的总动量等于作用后的总动量).
(系统内一个物体的动量变化与另一物体的动量变化等大反向)
(系统总动量的变化量为零)
二、动量守恒定律
3、守恒的正确理解:
(1)系统动量守恒不只是系统初末状态的动量相同,而是整个相互作
用的过程任何一时刻的动量都不变。
(2)系统动量守恒是矢量守恒不是标量守恒(和机械能守恒不同)
即一维碰撞前提下,系统初末动量的运算要求代入符号运算
已知 m1=1kg,m2=1kg,v1=2m/s,v2=-2m/s,
v1′=0,v2′=0,
已知 m1=4kg,m2=1kg,v1=v2=0,
v1′=-1m/s,v2′=4m/s,
已知 m1=4kg,m2=2kg,v1=4m/s,v2=2m/s,
v1′=2m/s,v2′=6m/s,
求出以下系统初末动量,并判断系统动量是否守恒?机械能是否守恒?
动量一增一减
动量都减少
动量都增加
4、守恒条件的理解:
(1)理想条件:系统不受外力作用或F合外=0
(2)近似条件:系统所受外力之和不为零,但系统的内力
远大于外力,外力可以忽略不计,如:碰撞、爆炸瞬间
(3)方向条件:系统受外力,且不能忽略,但在某一方向上所受外力为0, 则系统在该方向上动量守恒,
系统不受外力作用或F合外=0
5、判断不守恒的方法:
(1)条件法:合外力不为零且和内力接近
(2)系统动量构成法:一个物体动量不变另一个物体动量变化
地面光滑
6、动量守恒定律四性 :
(1)系统性:描述的对象是由两个以上的物体构成的系统 。
(2)矢量性 :若各物体相互作用前后在同一直线上,应首先选定正方向 。
(3)相对性 :表达式中各速度必须相对同一参考系。一般以地面为参考系。
(4)同时性 :初态动量的速度v1、v2都应该是互相作用前同一时刻的瞬时速度,末态动量中的速度v'1、v'2都必须是相互作用后同一时刻的瞬时速度。
①动量守恒定律不仅适用于正碰,也适用于斜碰;不仅适用于碰撞(时间较短),也适用于任何形式的相互作用(时间可以较长);不仅适用于两个物体组成的系统,也适用于两个以上物体组成的系统。
7、适用范围:
②定律既适用于宏观物体的相互作用,也适用于微观粒子的相互作用,不管是低速还是高速问题均适用。
机械能守恒定律 动量守恒定律
研究对象
守恒条件
守恒性质
适用范围
联系
注 意
8、机械能守恒和动量守恒的比较:
单个、或相互作用的物体组成的系统
相互作用的物体组成的系统
只有重力或弹力做功,其他力不做功
系统不受外力或所受合外力等于零
标量守恒(不考虑方向性)
矢量守恒(规定正方向)
都可以用实验来验证,因此它们都是实验规律。
爆炸、碰撞、反冲相互作用现象中,因F内>>F外,动量是守恒的,
但很多情况下有其它力(内力)做功,有其他形式能量转化为机械能,机械能不守恒.
仅限于宏观、低速领域
到目前为止物理学研究的一切领域
两小车在相互作用的运动过程中,相互排斥的磁力属于内力,整个系统的外力即重力和支持力的和为零,所以系统动量守恒。
思考∶在光滑水平面上有两个载有磁铁相向运动的小车,两小车组成的系统动量守恒吗
1、磁铁-小车
如果水平面为粗糙的,系统动量还守恒吗?
1.守恒对象?
2.守恒过程?
3.外力如何?
外力不为零,不守恒
三、动量守恒的判断
如图,静止的两辆小车用细线相连,中间有一个压缩了的轻质弹簧。烧断线后,由于弹力作用,两辆小车分别向左、右运动,两小车与弹簧组成的系统动量是否守恒?
两小车在运动过程中,弹簧弹力属于内力,整个系统的外力即重力和支持力的和为零,所以系统动量守恒。
2、小车-弹簧-小车
动量为矢量,矢量守恒,两小车的动量方向相反,动量的矢量和仍然为0
问题:两辆小车分别向左、右运动,它们都获得了动量,它们的总动量不是增加了吗,怎么会守恒呢?
1.守恒对象?
2.守恒过程?
3.外力如何?
内力
3、子弹-木块
子弹沿水平方向射入光滑水平桌面上的木块后,一起滑行,
①进入瞬间:系统动量守恒吗?
②一起滑行:系统动量怎样?
若桌面粗糙,结果如何
合外力为零,守恒;
合力功不为零,机械能不守恒
合外力为零,动量不转移,不变
内力远大于外力,动量守恒,
机械能不守恒
外力不能忽略,动量减少
①进入时:系统动量守恒吗?
②一起滑行时:系统动量怎么样?
所以,从进入到一起滑行全程系统动量不变,求末速度时直接动量守恒
所以,求末速度时,先动量守恒后动能定理
子弹A沿水平方向射入水平桌面上的木块B后,一起压缩弹簧压缩到最短。
4、子弹-木块-弹簧
①桌面光滑、进入过程、子弹和木块系统动量怎样?
②桌面粗糙、进入过程、子弹和木块系统动量怎样?
内力远大于外力(摩擦力)动量守恒
③桌面光滑、共速后、子弹和木块系统动量怎样?
外力(弹簧弹力)不能忽略,动量不守恒,但子弹、木块、弹簧系统机械能守恒
A
B
子弹射入木块的过程,时间极短暂,可认为弹簧仍保持原长,
此瞬间子弹与木块的摩擦为内力,系统合外力为零,
系统动量守恒,
思想方法:理想模型法,抓住重要因素忽略次要因素
子弹沿水平方向射入光滑水平桌面上的木块A后,一起压缩弹簧推动木块B直到弹簧最短。
5、子弹-木块1-弹簧-木块2
(1)子弹和木块A动量_____,机械能_______.
A
B
A
B
A
B
处理方法:弹簧长度不变,B木块未动
1.对象
2.过程
3.外力
(1)子弹和木块A动量________,机械能_______.
(2)子弹、木块A、木块B和弹簧动量______,机械能_______.
守恒
守恒
不守恒
不守恒
不守恒
守恒
斜面置于光滑水平面上,木块沿光滑斜面滑下,则木块与斜面组成的系统受到几个作用力?哪些力是内力?哪些是外力?系统动量守恒吗?
竖直方向失重:N<(M+m)g 系统动量不守恒。
N
Mg
mg
N1
N’1
思考:斜面粗糙但地面仍然光滑,系统水平方向动量还守恒吗?
系统水平方向不受外力作用,水平方向动量守恒
6、斜面-滑块
思考:在物块下滑的过程中系统水平方向动量守恒吗?
滑块和斜面间的摩擦为内力,系统水平方向动量守恒
在光滑的水平面上有一辆平板车,一个人站在车上用大锤敲打车的左端,如图所示,在连续地敲打下,这辆车能持续地向右运动吗?说明理由.
人、车系统水平方向不受外力作用,水平方向动量守恒 ,系统初动量为零, 任何一时刻系统动量矢量和必定都为零,当锤向左运动,小车就向右运动,大锤向右运动,小车向左运动,铁锤静止,小车也静止, 所以在水平面上左、右往返运动.车不会持续地向右驶去.
7、铁锤-小车
例题2、如图所示,气球与绳梯的质量为M,气球的绳梯上站着一个质量为m的人,原来整个系统处于静止状态,若空气阻力不计,当人沿绳梯相对地面向上爬时,对于整个系统来说动量是否守恒 为什么
人、气球系统静止时,重力平衡浮力,合外力为零,人向上爬行时,相互作用内力变化,重力浮力未变, 系统动量守恒,任何一时刻系统动量矢量和必定都为零,当人向上运动,气球就向下运动。
8、人-气球
如果整个系统开始一起加速上升状态,人往上爬行时,系统动量还守恒吗?
【例题1】在光滑水平面上有甲、乙两小球,它们的质量分别为1kg和4kg,甲球以10m/s的速度向左运动,乙球以5m/s的速度向右运动,两球发生正碰后,乙球以1m/s的速度继续向右运动。求:
(1)甲球碰撞后的速度
(2)甲、乙两球各自受到的冲量
相向守恒
相向运动碰撞时,一般以系统动量方向(较大动量方向)为正方向
答案:(1)6m/s (2)16NS ; -16NS
四、动量守恒的简单计算
【例题2】如图所示,质量为0.5 kg的小球在离车底面高度20 m处以一定的初速度向左平抛,落在以7.5 m/s的速度沿光滑的水平面向右匀速行驶的敞篷小车中,小车的底面上涂有一层油泥,车与油泥的总质量为4 kg,若小球在落在车的底面前瞬间的速度是25 m/s,则当小球和小车相对静止时,小车的速度是(g=10 m/s2)( )
A.5 m/s B.4 m/s
C.8.5 m/s D.9.5 m/s
A
方向守恒
只在水平方向守恒时,系统竖直方向都有超失重,即竖直方向合力不为零
【例题3】粗糙的水平地面上静止一质量为M的木块,一质量为m的子弹以初速度大小为v0沿水平方向射入木块,并未击穿,已知地面的动摩擦因数为μ,求:
(1)木块的最大速度
(2)木块在地面上滑行的位移
子弹木块处理方法:
(1)子弹进入瞬间,木块认为不动,系统机械能不守恒,动量守恒。
(2)一起减速滑行,系统动量不守恒,机械能转化为内能。
近似守恒
答案:(1)mv0/(m+M) (2)(mv0)2/2μ(M+m)2g
【例题1】一玩具机器人手持一小球站在一辆静止在光滑水平面上的小车上。小车和玩具机器人的总质量为4kg,小球质量为2kg。
(1)当机器人以相对地面为2m/s的速度水平向右抛出小球,求抛出小球后小车的速度
(2)当机器人以相对小车为2m/s的速度水平向右抛出小球,求抛出小球后小车的速度
v
答案:(1)-1m/s ,方向水平向左
(2)-0.67m/s ,方向水平向左
(1)动量守恒式中的速度都是相对地面的速度,要统一参考系。
(2)VA对B=VA对地-VB对地
(3)反冲模型问题中,立式求解时转移式方向易出错,宜用守恒式
守恒中的参考系问题
4、写出动量守恒表达式,求解计算
应用动量守恒定律解题的步骤:
1、对对应的过程选取正确和恰当的研究对象(系统)
3、统一参考系,选取正方向。确定各物体的初、末动量
2、受力分析,判断系统动量是否守恒或系统某方向是否动量守恒
在下列几种现象中,动量守恒的是( )
A、在静止的光滑水平面上,车上的人从车头走到车尾
B、水平放置的轻弹簧,一端固定于墙上,另一端与置于光滑水平面上的物体相连,开始时弹簧已有伸长,放手后物体在弹力的作用下运动
C、甲、乙两队进行拔河比赛,甲队获胜
D、汽车拉着拖车在平直的公路上做匀速直线运动,某时刻拖车突然脱钩离开汽车,由于司机没有发觉而保持汽车的牵引力不变,在拖车没有停下来的任何一段时间
AD
课堂练习
谢谢 再见!
第一章 动量守恒定律
1.3.1 动量守恒定律
F·Δt= mv' – mv0=Δp
单个物体动量变化的原因是合外力的冲量所致
相互碰撞的两物体动量都发生变化,但动量的总量保持不变
温故知新
动量的总量为什么会保持不变?
动量守恒要满足什么条件吗?
为什么会都发生变化?
注意:内力和外力的区分依赖于系统的选取,只有在确定了系统后,才能确定内力和外力。
系统:我们把两个(或多个)相互作用的物体构成的整体叫做一个力学系统。系统可按解决问题的需要灵活选取。
内力:系统中物体间的相互作用力叫做内力。
外力:系统以外的物体施加给系统内任何一个物体的力,叫做外力。
一、基本概念
选ABC为系统:A与C、B与C之间的摩擦力为内力还是外力?
选AB为系统:A与C、B与C之间的摩擦力为内力还是外力?
物理情景:在光滑水平面上做匀速运动的两个物体A、B,质量分别为m1和m2,沿着同一直线向相同的方向运动(一维碰撞),速度分别是v1、v2,且v2>v1。当B追上了A时发生碰撞。碰撞后A、B的速度分别为v1′和v2′。
碰撞过程
碰撞前
碰撞后
问题1:(谁的动量守恒)A物体、B物体、还是系统?
系统
问题2:(什么过程守恒)碰前、碰撞过程、碰后?
碰撞过程
问题3:碰撞过程物体A、B受到哪些力的冲量?
m2
m1
G1
N1
N2
G2
F2
F1
B
v2
m2
A
v1
m1
B
v2'
m2
A
v1'
m1
碰撞过程
对A应用动量定理:
对B应用动量定理:
根据牛顿第三定律:
得
两个物体碰撞后的动量之矢量和等于碰撞前的动量之矢量和。
F1
F2
m2
m1
动量守恒定律的推导
F1改变m1的动量
F2改变m2的动量
F1、F2不改变系统动量
碰撞过程
两个碰撞物体外部作用力的矢量和为0的情况下动量守恒。
思考:A、B系统,哪些力是内力?内力作用效果如何?
外力矢量和为零时,外力冲量为零,系统动量不变
守恒条件分析
思考:A、B系统,哪些力是外力?作用效果如何?外力的矢量和是多少?
内力只改变单个物体动量,不改变系统总动量。
外力既改变单个物体动量,也改变系统总动量。
m2
m1
G1
N1
N2
G2
F2
F1
如果一个系统不受外力,或者所受外力的矢量和为0,
这个系统的总动量保持不变。这就是动量守恒定律。
1.内容:
2.表达式:
(3)Δp=0
(1)p=p′或m1v1+m2v2=m1v1′+m2v2′
(2)Δp1=-Δp2 或 m1Δv1=-m2Δv2
(系统作用前的总动量等于作用后的总动量).
(系统内一个物体的动量变化与另一物体的动量变化等大反向)
(系统总动量的变化量为零)
二、动量守恒定律
3、守恒的正确理解:
(1)系统动量守恒不只是系统初末状态的动量相同,而是整个相互作
用的过程任何一时刻的动量都不变。
(2)系统动量守恒是矢量守恒不是标量守恒(和机械能守恒不同)
即一维碰撞前提下,系统初末动量的运算要求代入符号运算
已知 m1=1kg,m2=1kg,v1=2m/s,v2=-2m/s,
v1′=0,v2′=0,
已知 m1=4kg,m2=1kg,v1=v2=0,
v1′=-1m/s,v2′=4m/s,
已知 m1=4kg,m2=2kg,v1=4m/s,v2=2m/s,
v1′=2m/s,v2′=6m/s,
求出以下系统初末动量,并判断系统动量是否守恒?机械能是否守恒?
动量一增一减
动量都减少
动量都增加
4、守恒条件的理解:
(1)理想条件:系统不受外力作用或F合外=0
(2)近似条件:系统所受外力之和不为零,但系统的内力
远大于外力,外力可以忽略不计,如:碰撞、爆炸瞬间
(3)方向条件:系统受外力,且不能忽略,但在某一方向上所受外力为0, 则系统在该方向上动量守恒,
系统不受外力作用或F合外=0
5、判断不守恒的方法:
(1)条件法:合外力不为零且和内力接近
(2)系统动量构成法:一个物体动量不变另一个物体动量变化
地面光滑
6、动量守恒定律四性 :
(1)系统性:描述的对象是由两个以上的物体构成的系统 。
(2)矢量性 :若各物体相互作用前后在同一直线上,应首先选定正方向 。
(3)相对性 :表达式中各速度必须相对同一参考系。一般以地面为参考系。
(4)同时性 :初态动量的速度v1、v2都应该是互相作用前同一时刻的瞬时速度,末态动量中的速度v'1、v'2都必须是相互作用后同一时刻的瞬时速度。
①动量守恒定律不仅适用于正碰,也适用于斜碰;不仅适用于碰撞(时间较短),也适用于任何形式的相互作用(时间可以较长);不仅适用于两个物体组成的系统,也适用于两个以上物体组成的系统。
7、适用范围:
②定律既适用于宏观物体的相互作用,也适用于微观粒子的相互作用,不管是低速还是高速问题均适用。
机械能守恒定律 动量守恒定律
研究对象
守恒条件
守恒性质
适用范围
联系
注 意
8、机械能守恒和动量守恒的比较:
单个、或相互作用的物体组成的系统
相互作用的物体组成的系统
只有重力或弹力做功,其他力不做功
系统不受外力或所受合外力等于零
标量守恒(不考虑方向性)
矢量守恒(规定正方向)
都可以用实验来验证,因此它们都是实验规律。
爆炸、碰撞、反冲相互作用现象中,因F内>>F外,动量是守恒的,
但很多情况下有其它力(内力)做功,有其他形式能量转化为机械能,机械能不守恒.
仅限于宏观、低速领域
到目前为止物理学研究的一切领域
两小车在相互作用的运动过程中,相互排斥的磁力属于内力,整个系统的外力即重力和支持力的和为零,所以系统动量守恒。
思考∶在光滑水平面上有两个载有磁铁相向运动的小车,两小车组成的系统动量守恒吗
1、磁铁-小车
如果水平面为粗糙的,系统动量还守恒吗?
1.守恒对象?
2.守恒过程?
3.外力如何?
外力不为零,不守恒
三、动量守恒的判断
如图,静止的两辆小车用细线相连,中间有一个压缩了的轻质弹簧。烧断线后,由于弹力作用,两辆小车分别向左、右运动,两小车与弹簧组成的系统动量是否守恒?
两小车在运动过程中,弹簧弹力属于内力,整个系统的外力即重力和支持力的和为零,所以系统动量守恒。
2、小车-弹簧-小车
动量为矢量,矢量守恒,两小车的动量方向相反,动量的矢量和仍然为0
问题:两辆小车分别向左、右运动,它们都获得了动量,它们的总动量不是增加了吗,怎么会守恒呢?
1.守恒对象?
2.守恒过程?
3.外力如何?
内力
3、子弹-木块
子弹沿水平方向射入光滑水平桌面上的木块后,一起滑行,
①进入瞬间:系统动量守恒吗?
②一起滑行:系统动量怎样?
若桌面粗糙,结果如何
合外力为零,守恒;
合力功不为零,机械能不守恒
合外力为零,动量不转移,不变
内力远大于外力,动量守恒,
机械能不守恒
外力不能忽略,动量减少
①进入时:系统动量守恒吗?
②一起滑行时:系统动量怎么样?
所以,从进入到一起滑行全程系统动量不变,求末速度时直接动量守恒
所以,求末速度时,先动量守恒后动能定理
子弹A沿水平方向射入水平桌面上的木块B后,一起压缩弹簧压缩到最短。
4、子弹-木块-弹簧
①桌面光滑、进入过程、子弹和木块系统动量怎样?
②桌面粗糙、进入过程、子弹和木块系统动量怎样?
内力远大于外力(摩擦力)动量守恒
③桌面光滑、共速后、子弹和木块系统动量怎样?
外力(弹簧弹力)不能忽略,动量不守恒,但子弹、木块、弹簧系统机械能守恒
A
B
子弹射入木块的过程,时间极短暂,可认为弹簧仍保持原长,
此瞬间子弹与木块的摩擦为内力,系统合外力为零,
系统动量守恒,
思想方法:理想模型法,抓住重要因素忽略次要因素
子弹沿水平方向射入光滑水平桌面上的木块A后,一起压缩弹簧推动木块B直到弹簧最短。
5、子弹-木块1-弹簧-木块2
(1)子弹和木块A动量_____,机械能_______.
A
B
A
B
A
B
处理方法:弹簧长度不变,B木块未动
1.对象
2.过程
3.外力
(1)子弹和木块A动量________,机械能_______.
(2)子弹、木块A、木块B和弹簧动量______,机械能_______.
守恒
守恒
不守恒
不守恒
不守恒
守恒
斜面置于光滑水平面上,木块沿光滑斜面滑下,则木块与斜面组成的系统受到几个作用力?哪些力是内力?哪些是外力?系统动量守恒吗?
竖直方向失重:N<(M+m)g 系统动量不守恒。
N
Mg
mg
N1
N’1
思考:斜面粗糙但地面仍然光滑,系统水平方向动量还守恒吗?
系统水平方向不受外力作用,水平方向动量守恒
6、斜面-滑块
思考:在物块下滑的过程中系统水平方向动量守恒吗?
滑块和斜面间的摩擦为内力,系统水平方向动量守恒
在光滑的水平面上有一辆平板车,一个人站在车上用大锤敲打车的左端,如图所示,在连续地敲打下,这辆车能持续地向右运动吗?说明理由.
人、车系统水平方向不受外力作用,水平方向动量守恒 ,系统初动量为零, 任何一时刻系统动量矢量和必定都为零,当锤向左运动,小车就向右运动,大锤向右运动,小车向左运动,铁锤静止,小车也静止, 所以在水平面上左、右往返运动.车不会持续地向右驶去.
7、铁锤-小车
例题2、如图所示,气球与绳梯的质量为M,气球的绳梯上站着一个质量为m的人,原来整个系统处于静止状态,若空气阻力不计,当人沿绳梯相对地面向上爬时,对于整个系统来说动量是否守恒 为什么
人、气球系统静止时,重力平衡浮力,合外力为零,人向上爬行时,相互作用内力变化,重力浮力未变, 系统动量守恒,任何一时刻系统动量矢量和必定都为零,当人向上运动,气球就向下运动。
8、人-气球
如果整个系统开始一起加速上升状态,人往上爬行时,系统动量还守恒吗?
【例题1】在光滑水平面上有甲、乙两小球,它们的质量分别为1kg和4kg,甲球以10m/s的速度向左运动,乙球以5m/s的速度向右运动,两球发生正碰后,乙球以1m/s的速度继续向右运动。求:
(1)甲球碰撞后的速度
(2)甲、乙两球各自受到的冲量
相向守恒
相向运动碰撞时,一般以系统动量方向(较大动量方向)为正方向
答案:(1)6m/s (2)16NS ; -16NS
四、动量守恒的简单计算
【例题2】如图所示,质量为0.5 kg的小球在离车底面高度20 m处以一定的初速度向左平抛,落在以7.5 m/s的速度沿光滑的水平面向右匀速行驶的敞篷小车中,小车的底面上涂有一层油泥,车与油泥的总质量为4 kg,若小球在落在车的底面前瞬间的速度是25 m/s,则当小球和小车相对静止时,小车的速度是(g=10 m/s2)( )
A.5 m/s B.4 m/s
C.8.5 m/s D.9.5 m/s
A
方向守恒
只在水平方向守恒时,系统竖直方向都有超失重,即竖直方向合力不为零
【例题3】粗糙的水平地面上静止一质量为M的木块,一质量为m的子弹以初速度大小为v0沿水平方向射入木块,并未击穿,已知地面的动摩擦因数为μ,求:
(1)木块的最大速度
(2)木块在地面上滑行的位移
子弹木块处理方法:
(1)子弹进入瞬间,木块认为不动,系统机械能不守恒,动量守恒。
(2)一起减速滑行,系统动量不守恒,机械能转化为内能。
近似守恒
答案:(1)mv0/(m+M) (2)(mv0)2/2μ(M+m)2g
【例题1】一玩具机器人手持一小球站在一辆静止在光滑水平面上的小车上。小车和玩具机器人的总质量为4kg,小球质量为2kg。
(1)当机器人以相对地面为2m/s的速度水平向右抛出小球,求抛出小球后小车的速度
(2)当机器人以相对小车为2m/s的速度水平向右抛出小球,求抛出小球后小车的速度
v
答案:(1)-1m/s ,方向水平向左
(2)-0.67m/s ,方向水平向左
(1)动量守恒式中的速度都是相对地面的速度,要统一参考系。
(2)VA对B=VA对地-VB对地
(3)反冲模型问题中,立式求解时转移式方向易出错,宜用守恒式
守恒中的参考系问题
4、写出动量守恒表达式,求解计算
应用动量守恒定律解题的步骤:
1、对对应的过程选取正确和恰当的研究对象(系统)
3、统一参考系,选取正方向。确定各物体的初、末动量
2、受力分析,判断系统动量是否守恒或系统某方向是否动量守恒
在下列几种现象中,动量守恒的是( )
A、在静止的光滑水平面上,车上的人从车头走到车尾
B、水平放置的轻弹簧,一端固定于墙上,另一端与置于光滑水平面上的物体相连,开始时弹簧已有伸长,放手后物体在弹力的作用下运动
C、甲、乙两队进行拔河比赛,甲队获胜
D、汽车拉着拖车在平直的公路上做匀速直线运动,某时刻拖车突然脱钩离开汽车,由于司机没有发觉而保持汽车的牵引力不变,在拖车没有停下来的任何一段时间
AD
课堂练习
谢谢 再见!
