人教版八年级下册18.1.2 平行四边形的判定课件(共20张PPT)
文档属性
| 名称 | 人教版八年级下册18.1.2 平行四边形的判定课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 186.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 16:39:35 | ||
图片预览


文档简介
(共20张PPT)
第十八章 平行四边形
18.1.2 平行四边形判定
第1课时 平行四边形的判定(2)
情景引入
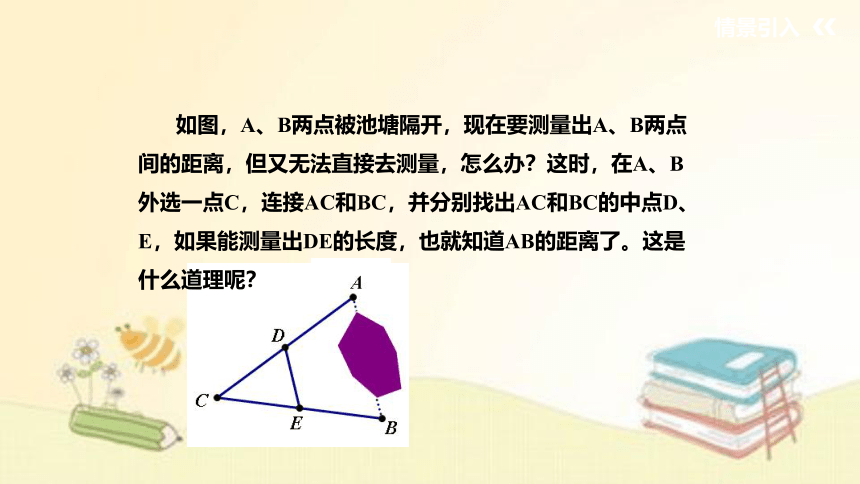
如图,A、B两点被池塘隔开,现在要测量出A、B两点间的距离,但又无法直接去测量,怎么办?这时,在A、B外选一点C,连接AC和BC,并分别找出AC和BC的中点D、E,如果能测量出DE的长度,也就知道AB的距离了。这是什么道理呢?
合作探究
我们知道,两组对分别平行或相等的是平行四边形。如果只考虑四边形的一组对边,它们满足什么条件时这个四边形能成为平行四边形呢?
我们知道,如果一个四边形是平行四边形,那么它的任意一组对边平行且相等.反过来,一组对边平行且相等的四边形是平行四边形吗?
活动1:探究一组对边平行且相等的四边形是平行
四边形
合作探究
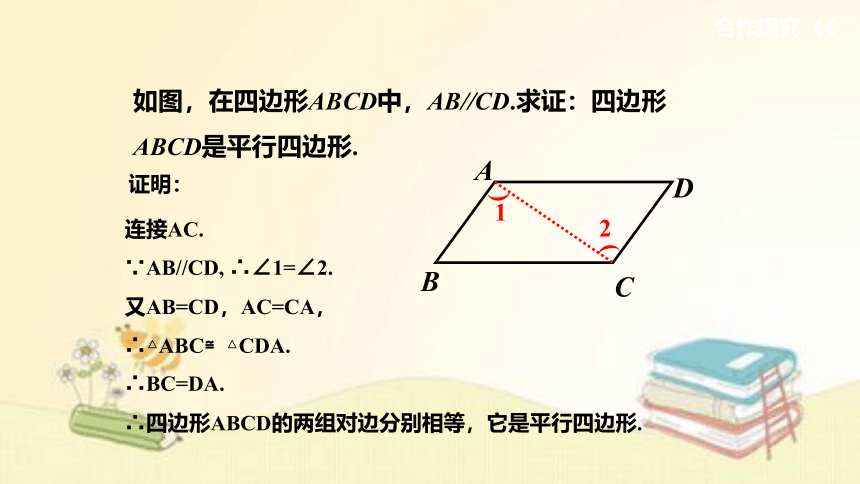
连接AC.
∵AB//CD, ∴∠1=∠2.
又AB=CD,AC=CA,
∴△ABC≌△CDA.
∴BC=DA.
∴四边形ABCD的两组对边分别相等,它是平行四边形.
D
A
B
C
如图,在四边形ABCD中,AB//CD.求证:四边形ABCD是平行四边形.
证明:
1
2
(
)
知识要点
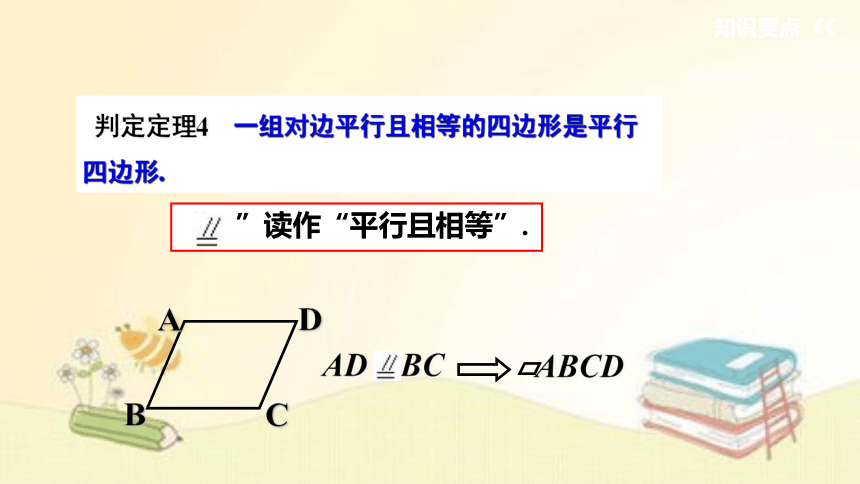
判定定理4 一组对边平行且相等的四边形是平行四边形.
A
B
C
D
ABCD
“ ”读作“平行且相等”.
AD BC
知识要点
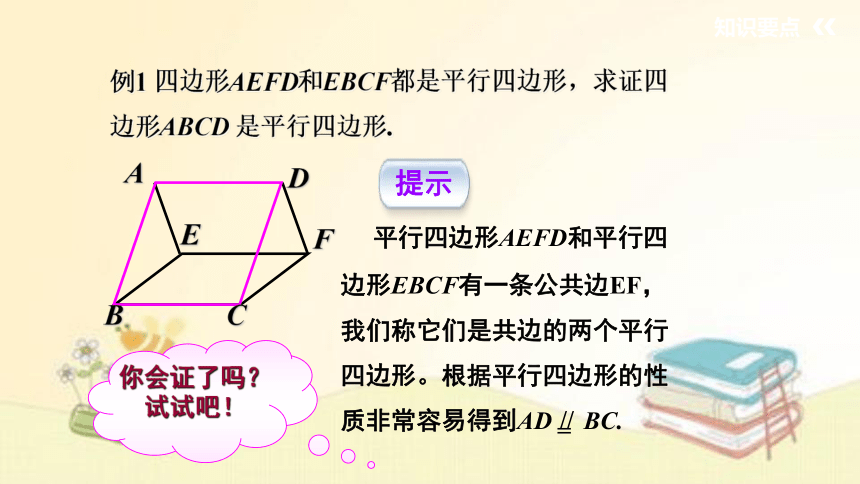
平行四边形AEFD和平行四边形EBCF有一条公共边EF,我们称它们是共边的两个平行四边形。根据平行四边形的性质非常容易得到AD BC.
//
=
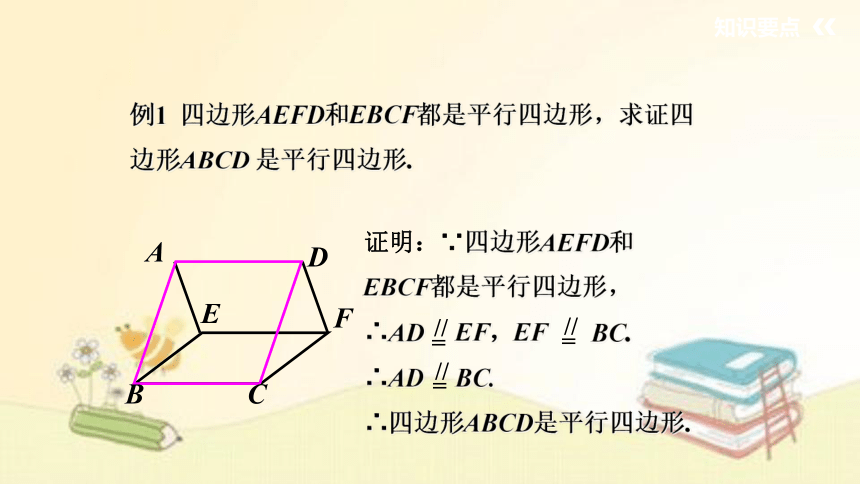
例1 四边形AEFD和EBCF都是平行四边形,求证四边形ABCD 是平行四边形.
A
B
C
D
E
F
你会证了吗?试试吧!
提示
知识要点
A
B
C
D
E
F
证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD EF,EF BC.
∴AD BC.
∴四边形ABCD是平行四边形.
//
=
//
=
//
=
例1 四边形AEFD和EBCF都是平行四边形,求证四边形ABCD 是平行四边形.
知识要点
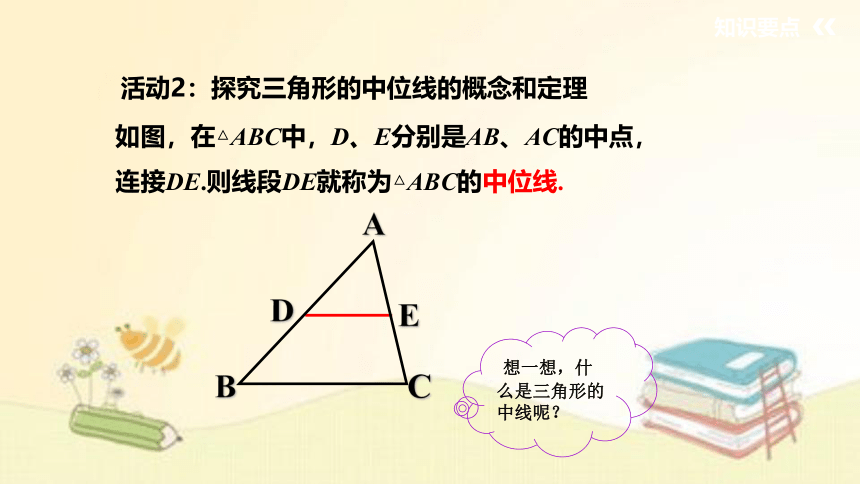
想一想,什么是三角形的中线呢?
A
B
C
D
E
如图,在△ABC中,D、E分别是AB、AC的中点,连接DE.则线段DE就称为△ABC的中位线.
活动2:探究三角形的中位线的概念和定理
知识要点
F
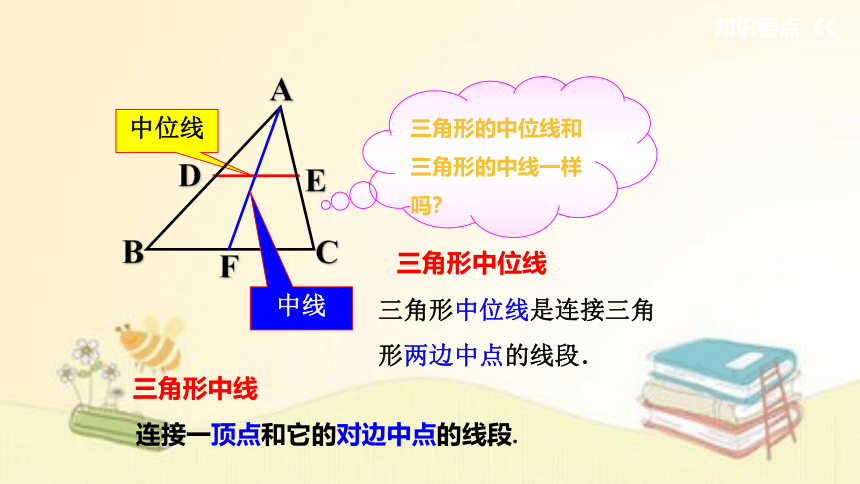
三角形的中位线和三角形的中线一样吗?
中位线
A
B
C
D
E
中线
连接一顶点和它的对边中点的线段.
三角形中位线
三角形中位线是连接三角形两边中点的线段.
三角形中线
知识要点
(1)一个三角形有几条中位线?你能画出来吗?
A
B
C
D
E
F
答:有三条,见图中中位线DE、DF、EF.
(2)请你猜想:三角形的中位线DE与BC有什么样的位置关系和数量关系呢?
猜想
思考
知识要点
已知:如图,D、E分别是△ABC的边AB、AC的中点,求证:
分析:要证明线段的倍分关系,可将DE加倍后证明与BC相等.从而转化为证明平行四边形的对边的关系, 于是可作辅助线,利用全等三角形来证明相应的边相等.
D
E
B
C
A
知识要点
证明:延长DE至F,使EF=DE,连接FC、DC、AF.
∵ AE=CE,
D
E
B
C
A
F
∴四边形DBCF是平行四边形.
∴DE∥BC,
∴四边形ADCF是平行四边形,
D
E
B
C
A
有什么发现呢?
知识要点
在△ABC中 AD=BD,AE=CE
我们把连接三角形两边中点的线段叫做三角形的中位线.
三角形中位线定理:
三角形的中位线平行于三角形的第三边,且等于第三边的一半.
A
B
C
D
E
几何格式:
DE∥BC
知识要点
原来如此
能测量出DE的长度,也就知道AB的距离了.这是什么道理呢?
答:这是根据三角形中位线的性质定理.
知识要点
例2 如图,在△ABC中,DE是中位线.
(1)若∠ADE=60°,则∠B= .
(2)若BC=8cm,则DE= cm.
A
B
C
D
E
(3)已知三角形三边分别为4、6、8,则连接该三角形各边中点所得的三角形的周长是 .
60°
4
9
重要发现
A
B
C
D
E
F
①中位线DE、EF、DF把△ABC
分成四个全等的三角形;有三
组共边的平行四边形,它们是
四边形ADFE和BDEF,四边形
BFED和CFDE,四边形ADFE
和DFCE.
②顶点是中点的三角形,我们称之为中点三角形;中点三角形的周长是原三角形的周长的一半.
重要发现
例3 (1)在△ABC中,BD、CE分别是边AC,AB上的中线,BD、CE相交于点O,H点M、N分别是OB、OC的中点,试猜想四边形DEMN是什么四边形?请加以证明.
答:四边形DEMN是平行四边形.
理由如下:
∵DE是△ABC的中位线
∴DE//BC,DE= BC.
∵MN是△OBC的中位线
∴MN//BC,MN= BC.
∴四边形DEMN是平行四边形.
课堂小结
判定定理4 一组对边平行且相等的四边形是平行四边形.
②已知一组对边相等,可以证另一组对边相等,构成判定定理1;也可证这组对边平行,构成判定定理4.
①已知一组对边平行,可以证另一组对边平行,即定义法;也可证这组对边相等,构成判定定理4.
平行四边形判定方法的选择方法
课堂小结
三角形中位线是三角形中重要线段,它与三角形中线不同.
三角形中位线具体应用时,可视具体情况选用其中一个关系或两个关系.熟悉三角形中位线基本图形,有时需要适当构造三角形中位线的条件是用好定理的条件.
三角形中位线定理:
三角形的中位线平行于三角形的第三边,且等于第三边的一半.
谢 谢!
第十八章 平行四边形
18.1.2 平行四边形判定
第1课时 平行四边形的判定(2)
情景引入
如图,A、B两点被池塘隔开,现在要测量出A、B两点间的距离,但又无法直接去测量,怎么办?这时,在A、B外选一点C,连接AC和BC,并分别找出AC和BC的中点D、E,如果能测量出DE的长度,也就知道AB的距离了。这是什么道理呢?
合作探究
我们知道,两组对分别平行或相等的是平行四边形。如果只考虑四边形的一组对边,它们满足什么条件时这个四边形能成为平行四边形呢?
我们知道,如果一个四边形是平行四边形,那么它的任意一组对边平行且相等.反过来,一组对边平行且相等的四边形是平行四边形吗?
活动1:探究一组对边平行且相等的四边形是平行
四边形
合作探究
连接AC.
∵AB//CD, ∴∠1=∠2.
又AB=CD,AC=CA,
∴△ABC≌△CDA.
∴BC=DA.
∴四边形ABCD的两组对边分别相等,它是平行四边形.
D
A
B
C
如图,在四边形ABCD中,AB//CD.求证:四边形ABCD是平行四边形.
证明:
1
2
(
)
知识要点
判定定理4 一组对边平行且相等的四边形是平行四边形.
A
B
C
D
ABCD
“ ”读作“平行且相等”.
AD BC
知识要点
平行四边形AEFD和平行四边形EBCF有一条公共边EF,我们称它们是共边的两个平行四边形。根据平行四边形的性质非常容易得到AD BC.
//
=
例1 四边形AEFD和EBCF都是平行四边形,求证四边形ABCD 是平行四边形.
A
B
C
D
E
F
你会证了吗?试试吧!
提示
知识要点
A
B
C
D
E
F
证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD EF,EF BC.
∴AD BC.
∴四边形ABCD是平行四边形.
//
=
//
=
//
=
例1 四边形AEFD和EBCF都是平行四边形,求证四边形ABCD 是平行四边形.
知识要点
想一想,什么是三角形的中线呢?
A
B
C
D
E
如图,在△ABC中,D、E分别是AB、AC的中点,连接DE.则线段DE就称为△ABC的中位线.
活动2:探究三角形的中位线的概念和定理
知识要点
F
三角形的中位线和三角形的中线一样吗?
中位线
A
B
C
D
E
中线
连接一顶点和它的对边中点的线段.
三角形中位线
三角形中位线是连接三角形两边中点的线段.
三角形中线
知识要点
(1)一个三角形有几条中位线?你能画出来吗?
A
B
C
D
E
F
答:有三条,见图中中位线DE、DF、EF.
(2)请你猜想:三角形的中位线DE与BC有什么样的位置关系和数量关系呢?
猜想
思考
知识要点
已知:如图,D、E分别是△ABC的边AB、AC的中点,求证:
分析:要证明线段的倍分关系,可将DE加倍后证明与BC相等.从而转化为证明平行四边形的对边的关系, 于是可作辅助线,利用全等三角形来证明相应的边相等.
D
E
B
C
A
知识要点
证明:延长DE至F,使EF=DE,连接FC、DC、AF.
∵ AE=CE,
D
E
B
C
A
F
∴四边形DBCF是平行四边形.
∴DE∥BC,
∴四边形ADCF是平行四边形,
D
E
B
C
A
有什么发现呢?
知识要点
在△ABC中 AD=BD,AE=CE
我们把连接三角形两边中点的线段叫做三角形的中位线.
三角形中位线定理:
三角形的中位线平行于三角形的第三边,且等于第三边的一半.
A
B
C
D
E
几何格式:
DE∥BC
知识要点
原来如此
能测量出DE的长度,也就知道AB的距离了.这是什么道理呢?
答:这是根据三角形中位线的性质定理.
知识要点
例2 如图,在△ABC中,DE是中位线.
(1)若∠ADE=60°,则∠B= .
(2)若BC=8cm,则DE= cm.
A
B
C
D
E
(3)已知三角形三边分别为4、6、8,则连接该三角形各边中点所得的三角形的周长是 .
60°
4
9
重要发现
A
B
C
D
E
F
①中位线DE、EF、DF把△ABC
分成四个全等的三角形;有三
组共边的平行四边形,它们是
四边形ADFE和BDEF,四边形
BFED和CFDE,四边形ADFE
和DFCE.
②顶点是中点的三角形,我们称之为中点三角形;中点三角形的周长是原三角形的周长的一半.
重要发现
例3 (1)在△ABC中,BD、CE分别是边AC,AB上的中线,BD、CE相交于点O,H点M、N分别是OB、OC的中点,试猜想四边形DEMN是什么四边形?请加以证明.
答:四边形DEMN是平行四边形.
理由如下:
∵DE是△ABC的中位线
∴DE//BC,DE= BC.
∵MN是△OBC的中位线
∴MN//BC,MN= BC.
∴四边形DEMN是平行四边形.
课堂小结
判定定理4 一组对边平行且相等的四边形是平行四边形.
②已知一组对边相等,可以证另一组对边相等,构成判定定理1;也可证这组对边平行,构成判定定理4.
①已知一组对边平行,可以证另一组对边平行,即定义法;也可证这组对边相等,构成判定定理4.
平行四边形判定方法的选择方法
课堂小结
三角形中位线是三角形中重要线段,它与三角形中线不同.
三角形中位线具体应用时,可视具体情况选用其中一个关系或两个关系.熟悉三角形中位线基本图形,有时需要适当构造三角形中位线的条件是用好定理的条件.
三角形中位线定理:
三角形的中位线平行于三角形的第三边,且等于第三边的一半.
谢 谢!
