人教版五年级下学期数学探索图形 课件(共20张PPT)
文档属性
| 名称 | 人教版五年级下学期数学探索图形 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 27.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
探索图形
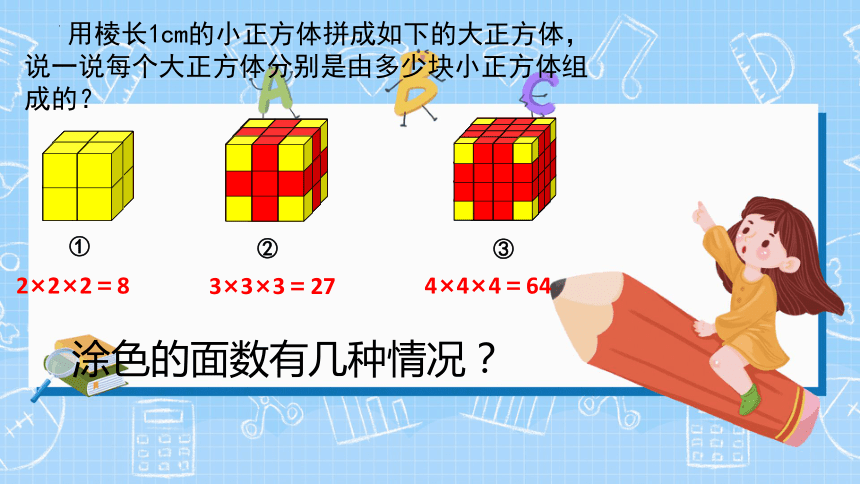
用棱长1cm的小正方体拼成如下的大正方体,
说一说每个大正方体分别是由多少块小正方体组
成的?
2×2×2=8
3×3×3=27
4×4×4=64
①
②
③
涂色的面数有几种情况?
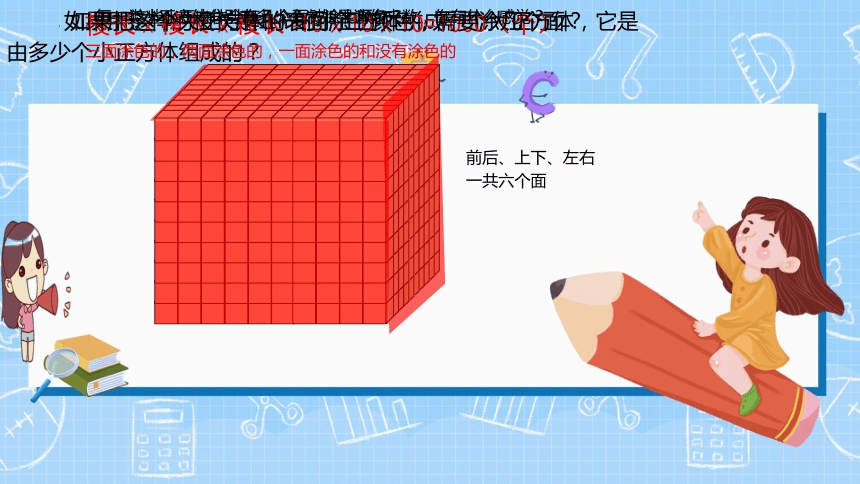
如果用这样的棱长是1cm的小正方体拼成一个大正方体,它是
由多少个小正方体组成的?
棱长x棱长x棱长=10x10x10=1000(个)
如果把这个大正方体的表面涂上颜色,需要涂几个面?
前后、上下、左右一共六个面
这些小正方体会有几个面被涂上颜色?
三面涂色的,两面涂色的,一面涂色的和没有涂色的
每一类小正方体分别有多少个?如果请你来数,你有什么感觉?
1、四人小组合作,利用学具探究两面涂色的小正方体的块数。
2、试着将发现的结果用列式的方法表示在“小组探究卡”的相应表格中。
小组探究:
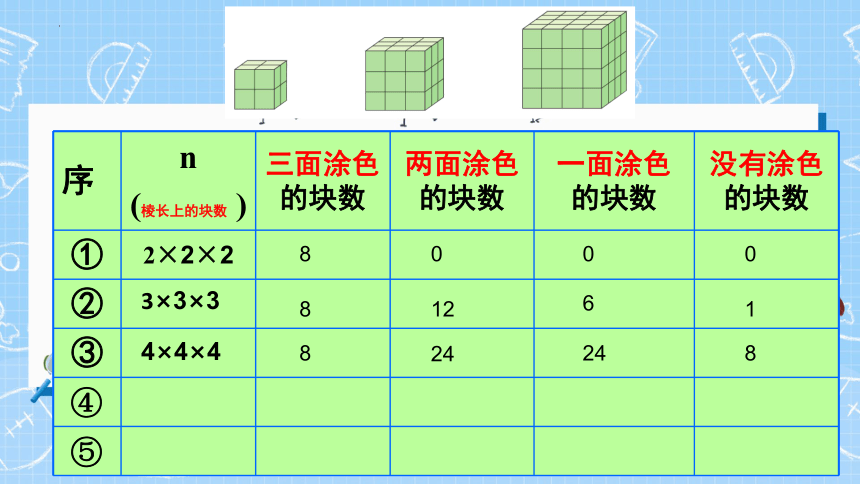
序 n (棱长上的块数 ) 三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
① 2×2×2
②
③
8
0
0
0
8
12
6
1
8
24
24
8
④
⑤
3×3×3
4×4×4
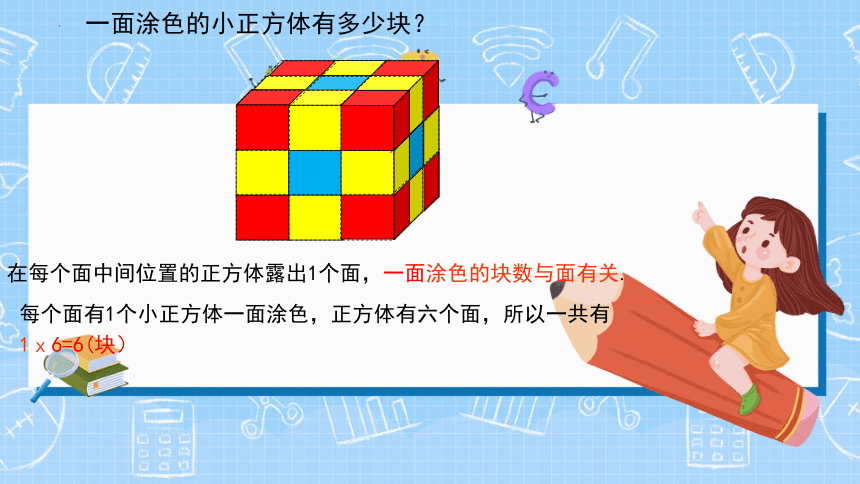
一面涂色的小正方体有多少块?
在每个面中间位置的正方体露出1个面,一面涂色的块数与面有关.
每个面有1个小正方体一面涂色,正方体有六个面,所以一共有1x6=6(块)
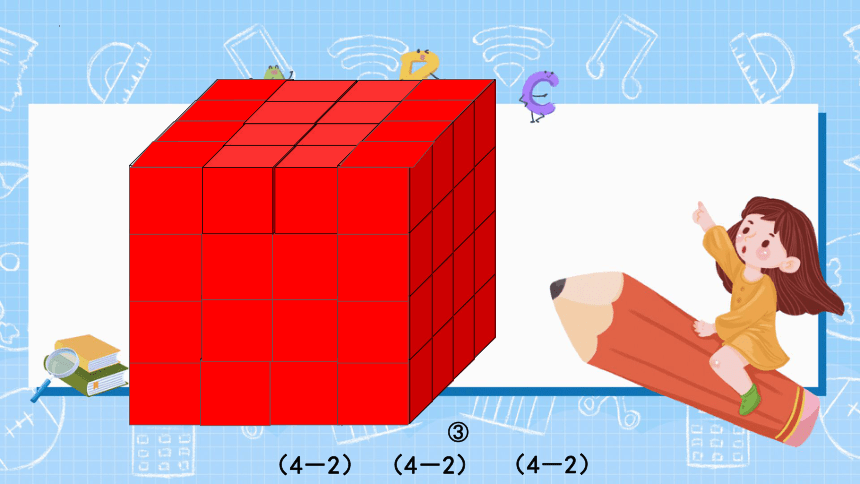
③
(4-2)
(4-2)
(4-2)
三面涂色的小正方体在原正方体的顶点处。
三面涂色、两面涂色、一面涂色的小正方体在原正方体的什么位置?
?
序 n (棱长上的块数 ) 三面涂色 的块数 两面涂色 的块数 一面涂色 的块数 没有涂色
的块数
2×2×2 8 0 0 0
3×3×3 8 12 6 1
4×4×4 8 24 24 8
5×5×5
6×6×6
36
54
27
48
96
64
按这样的规律摆下去,第④、⑤个正方体的结果会是怎样的呢?
①
②
③
④
⑤
8
8
通过刚才的学习,我们发现:三面涂色的块数与顶点数相同,两面涂色的块数与棱有关,一面涂色的块数与面有关,没有涂色的块数在里面。
12条棱有 个
2面涂色的小正方体。
(n-2)
×12
每条棱有 个
2面涂色的小正方体。
n-2
每条棱有n个小正方体
1、如果从下面的正方体中拿走一块三面涂色的小正方体,那么正 方体的表面积会( )
A变大 B 不变 C变小
2、如果从下面的正方体中拿走一块两面涂色的小正方体,那么正方体的表面积会( )
A变大 B 不变 C变小
3、如果从下面的正方体中拿走一块一面面涂色的小正方体,那么正方体的表面积会( )
A变小 B 不变 C变大
趣味题
B
A
C
没有涂色的块数是
(棱长-2)x(棱长-2)x(棱长-2),
一共有(4-2)x(4-2)x(4-2)=8(个)
②
(3-2)
(3-2)
(3-2)
正方体的棱长 3cm 4cm 5cm
没有涂色的个数
33
23
13
33=27
23=8
13=1
1
8
27
回顾探索和发现的过程,说说你的体会。
如果摆成下面的几何体,你会数吗?
课后练习
聪明出于勤奋,天才在于积累。
探索图形
用棱长1cm的小正方体拼成如下的大正方体,
说一说每个大正方体分别是由多少块小正方体组
成的?
2×2×2=8
3×3×3=27
4×4×4=64
①
②
③
涂色的面数有几种情况?
如果用这样的棱长是1cm的小正方体拼成一个大正方体,它是
由多少个小正方体组成的?
棱长x棱长x棱长=10x10x10=1000(个)
如果把这个大正方体的表面涂上颜色,需要涂几个面?
前后、上下、左右一共六个面
这些小正方体会有几个面被涂上颜色?
三面涂色的,两面涂色的,一面涂色的和没有涂色的
每一类小正方体分别有多少个?如果请你来数,你有什么感觉?
1、四人小组合作,利用学具探究两面涂色的小正方体的块数。
2、试着将发现的结果用列式的方法表示在“小组探究卡”的相应表格中。
小组探究:
序 n (棱长上的块数 ) 三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
① 2×2×2
②
③
8
0
0
0
8
12
6
1
8
24
24
8
④
⑤
3×3×3
4×4×4
一面涂色的小正方体有多少块?
在每个面中间位置的正方体露出1个面,一面涂色的块数与面有关.
每个面有1个小正方体一面涂色,正方体有六个面,所以一共有1x6=6(块)
③
(4-2)
(4-2)
(4-2)
三面涂色的小正方体在原正方体的顶点处。
三面涂色、两面涂色、一面涂色的小正方体在原正方体的什么位置?
?
序 n (棱长上的块数 ) 三面涂色 的块数 两面涂色 的块数 一面涂色 的块数 没有涂色
的块数
2×2×2 8 0 0 0
3×3×3 8 12 6 1
4×4×4 8 24 24 8
5×5×5
6×6×6
36
54
27
48
96
64
按这样的规律摆下去,第④、⑤个正方体的结果会是怎样的呢?
①
②
③
④
⑤
8
8
通过刚才的学习,我们发现:三面涂色的块数与顶点数相同,两面涂色的块数与棱有关,一面涂色的块数与面有关,没有涂色的块数在里面。
12条棱有 个
2面涂色的小正方体。
(n-2)
×12
每条棱有 个
2面涂色的小正方体。
n-2
每条棱有n个小正方体
1、如果从下面的正方体中拿走一块三面涂色的小正方体,那么正 方体的表面积会( )
A变大 B 不变 C变小
2、如果从下面的正方体中拿走一块两面涂色的小正方体,那么正方体的表面积会( )
A变大 B 不变 C变小
3、如果从下面的正方体中拿走一块一面面涂色的小正方体,那么正方体的表面积会( )
A变小 B 不变 C变大
趣味题
B
A
C
没有涂色的块数是
(棱长-2)x(棱长-2)x(棱长-2),
一共有(4-2)x(4-2)x(4-2)=8(个)
②
(3-2)
(3-2)
(3-2)
正方体的棱长 3cm 4cm 5cm
没有涂色的个数
33
23
13
33=27
23=8
13=1
1
8
27
回顾探索和发现的过程,说说你的体会。
如果摆成下面的几何体,你会数吗?
课后练习
聪明出于勤奋,天才在于积累。
