1.2.2直线的方程(3)——两点式、截距式(1)课件-2021-2022学年高二上学期数学苏教版(2019)选择性必修第一册(共19张PPT)
文档属性
| 名称 | 1.2.2直线的方程(3)——两点式、截距式(1)课件-2021-2022学年高二上学期数学苏教版(2019)选择性必修第一册(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 482.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 21:17:26 | ||
图片预览






文档简介
(共19张PPT)
直线的方程(3)
——两点式、截距式(1)
复习回顾
1、直线的点斜式方程
2、直线的斜截式方程
3、直线的点斜式方程和斜截式方程之间的关系
斜截式是点斜式的特殊情况,两者均不能表示斜率不存在即与x轴垂直的直线。
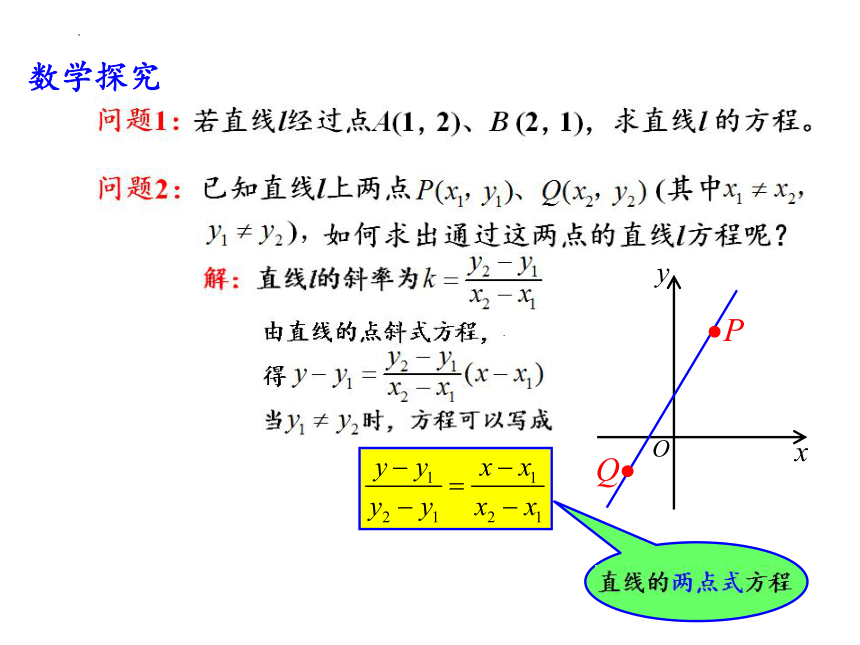
数学探究
数学建构
1、直线的两点式方程
(3)方程 能表示平面内
任意一条直线。
数学应用
类型一 利用两点式、截距式求直线方程
例1、分别求满足下列条件的直线l的方程
(1)直线l经过两点P1(1,2), P2(3,5);
(2)直线l经过两点P1(1,3), P2(2,3);
(3)直线l经过两点P1(3,2), P2(3,1);
(4)直线l经过两点P1(3,0), P2(0,2)。
(1)直接法:用直线方程的两点式直接求(公式!)
(2)间接法:先求出斜率,再用直线方程的点斜式求。
推荐间接法不易出错
思路点拨:
变式拓展
若直线l经过两点P1(a,0), P2(0,b)(ab≠0),试求直线l的
方程。
变形为
解:由直线的两点式方程,得
数学建构
2、直线的截距式方程
数学练习
求下列直线的斜率和直线在x轴和y轴上的截距。
(1) (2)x+2y=0
(3)7x-6y+4=0 (4)2y-7=0
数学建构
3、四种直线方程及其适用范围
数学练习
下列四个命题中正确的是( )
(A)经过定点P0 (x0,y0)的直线都可以用方程y-y0=k(x-x0)
表示;
(B)经过任意两个不同点P1 (x1,y1)、 P2 (x2,y2)的直线都可
以用方程(y-y1)(x2-x1) = (x-x1)(y2-y1)表示;
(C)不经过原点的直线都可以用方程 表示;
(D)经过定点的直线都可以用方程y=kx+b表示。
B
数学应用
类型二 直线方程形式的互化及应用
例2、由下列条件求直线的斜截式方程
(1)直线经过点P1 (2,1),P2 (0,-3);
(2)直线在x轴上的截距是2,在y轴上的截距是-3。
变式拓展
(1)已知直线mx + ny + 12 = 0在x轴,y轴上的截距分别是 –3
和4,求m,n的值;
(2)已知直线l在x轴上的截距比在y轴上的截距大1,且过定
点P(6,-2),求直线l的方程。
数学应用
例3、三角形的顶点是A (-5,0),B (3,-3),C (0,2),求
这个三角形三边所在直线方程。
类型三 三角形中有关直线方程的求解
x
y
o
BC:
AB:
AC:
数学应用
例4、求经过点(4,-3)且在两坐标轴上的截距相等的直线
方程。
类型四 关于直线在坐标轴上的截距问题研究
变式拓展
(1)求经过点(4,-3)且在两坐标轴上的截距互为相反数的直
线方程。
(2)求经过点(4,-3)且在两坐标轴上的截距互为倒数的直线
方程。
变式拓展
(3)求经过点(4,-3)且在x轴上的截距是在y轴上的截距的2倍
的直线方程。
(4)求经过点(4,-3)且在在x轴上的截距与在y轴上的截距之
比为2:1的直线方程。
题后反思
1、如果题目中出现直线在两坐标轴上的“截距相等”、
“截距互为相反数”、“在一坐标轴上的截距是另一坐
标轴上截距的m倍(m>0)”等条件时,若采用截距式求
直线方程,则一定要注意考虑“零截距”的情况;
2、直线与坐标轴截距相等问题的求解思路:
课堂检测
1、直线l过点B(0,2),且与x轴交于A点,若|AB|=4,求
直线 l的方程。
2、直线Ax + By + C=0在x轴和y轴上的截距分别是2和1,
则A: B:C=
3、经过点(– 4,3)且在两坐标轴上的截距相等的直线方程
为
★四种直线方程及其适用范围★
课堂小结
直线的方程(3)
——两点式、截距式(1)
复习回顾
1、直线的点斜式方程
2、直线的斜截式方程
3、直线的点斜式方程和斜截式方程之间的关系
斜截式是点斜式的特殊情况,两者均不能表示斜率不存在即与x轴垂直的直线。
数学探究
数学建构
1、直线的两点式方程
(3)方程 能表示平面内
任意一条直线。
数学应用
类型一 利用两点式、截距式求直线方程
例1、分别求满足下列条件的直线l的方程
(1)直线l经过两点P1(1,2), P2(3,5);
(2)直线l经过两点P1(1,3), P2(2,3);
(3)直线l经过两点P1(3,2), P2(3,1);
(4)直线l经过两点P1(3,0), P2(0,2)。
(1)直接法:用直线方程的两点式直接求(公式!)
(2)间接法:先求出斜率,再用直线方程的点斜式求。
推荐间接法不易出错
思路点拨:
变式拓展
若直线l经过两点P1(a,0), P2(0,b)(ab≠0),试求直线l的
方程。
变形为
解:由直线的两点式方程,得
数学建构
2、直线的截距式方程
数学练习
求下列直线的斜率和直线在x轴和y轴上的截距。
(1) (2)x+2y=0
(3)7x-6y+4=0 (4)2y-7=0
数学建构
3、四种直线方程及其适用范围
数学练习
下列四个命题中正确的是( )
(A)经过定点P0 (x0,y0)的直线都可以用方程y-y0=k(x-x0)
表示;
(B)经过任意两个不同点P1 (x1,y1)、 P2 (x2,y2)的直线都可
以用方程(y-y1)(x2-x1) = (x-x1)(y2-y1)表示;
(C)不经过原点的直线都可以用方程 表示;
(D)经过定点的直线都可以用方程y=kx+b表示。
B
数学应用
类型二 直线方程形式的互化及应用
例2、由下列条件求直线的斜截式方程
(1)直线经过点P1 (2,1),P2 (0,-3);
(2)直线在x轴上的截距是2,在y轴上的截距是-3。
变式拓展
(1)已知直线mx + ny + 12 = 0在x轴,y轴上的截距分别是 –3
和4,求m,n的值;
(2)已知直线l在x轴上的截距比在y轴上的截距大1,且过定
点P(6,-2),求直线l的方程。
数学应用
例3、三角形的顶点是A (-5,0),B (3,-3),C (0,2),求
这个三角形三边所在直线方程。
类型三 三角形中有关直线方程的求解
x
y
o
BC:
AB:
AC:
数学应用
例4、求经过点(4,-3)且在两坐标轴上的截距相等的直线
方程。
类型四 关于直线在坐标轴上的截距问题研究
变式拓展
(1)求经过点(4,-3)且在两坐标轴上的截距互为相反数的直
线方程。
(2)求经过点(4,-3)且在两坐标轴上的截距互为倒数的直线
方程。
变式拓展
(3)求经过点(4,-3)且在x轴上的截距是在y轴上的截距的2倍
的直线方程。
(4)求经过点(4,-3)且在在x轴上的截距与在y轴上的截距之
比为2:1的直线方程。
题后反思
1、如果题目中出现直线在两坐标轴上的“截距相等”、
“截距互为相反数”、“在一坐标轴上的截距是另一坐
标轴上截距的m倍(m>0)”等条件时,若采用截距式求
直线方程,则一定要注意考虑“零截距”的情况;
2、直线与坐标轴截距相等问题的求解思路:
课堂检测
1、直线l过点B(0,2),且与x轴交于A点,若|AB|=4,求
直线 l的方程。
2、直线Ax + By + C=0在x轴和y轴上的截距分别是2和1,
则A: B:C=
3、经过点(– 4,3)且在两坐标轴上的截距相等的直线方程
为
★四种直线方程及其适用范围★
课堂小结
