1.4.2用空间向量研究距离、夹角问题 (第一课时)(共17张PPT)
文档属性
| 名称 | 1.4.2用空间向量研究距离、夹角问题 (第一课时)(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 21:18:39 | ||
图片预览





文档简介
(共17张PPT)
第一章
1.4.1用空间向量研究直线、平面位置关系
空间中直线、平面的平行
用空间向量研究距离、夹角问题
学习目标
1.能利用投影向量得到点到直线、点到平面的距离公式,
2.结合一些具体的距离问题的解决归纳纳用空间向量解决立体几何问题的“三步曲”.
教学重难点
重点:利用投影向量推导点到直线的距离公式和点到平面的距离公式.
难点:利用投影向量统一研究空间距离问题.
我们知道,立体几何中的距离问题包括点到直线、点到平面、两条平行直线,以及两个平行平面的距离问题等.如何用空间向量解决这些距离问题呢
下面我们先研究用向量方法求直线l外一点P到直线l的距离.
用空间向量研究距离、夹角问题
用空间向量研究距离、夹角问题
知识点一 点到直线的距离
已知直线l的单位方向向量为u,A是直线l上的定点,P是直线l外一点.如何利用这些条件求点P到直线l的距离
探究
如图,向量AP在直线l上的投影向量为,则APQ是直角三角形,因为A,P都是定点,所以||,与u的夹角∠PAQ都是确定的.于是可求||.再利用勾股定理,可以求出点P到直线l的距离PQ.
设=a,则向量在直线l上的投影向量=(au)u.
在RtAPQ中,由勾股定理,得
PQ = =.
知识点二 两平行线距离
思考
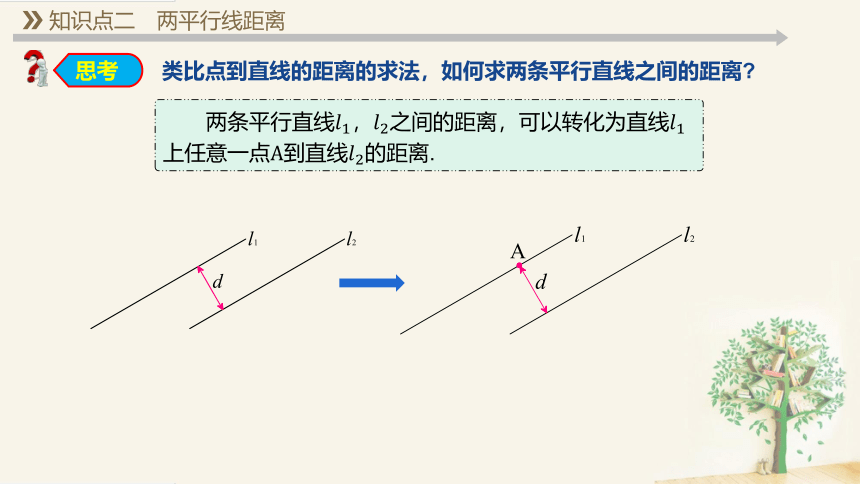
两条平行直线,之间的距离,可以转化为直线上任意一点A到直线的距离.
类比点到直线的距离的求法,如何求两条平行直线之间的距离
知识点三 点到平面距离
思考
类比点到直线的距离的求法,如何求平面α外一点P到平面α的距离
第一步
第二步
第三步
第四步
确定平面α的法向量为n
选择“参考向量”
确定“参考向量”向法向量n的投影
求投影向量的模长,得到
PQ=.
知识点二 两平行线距离
思考
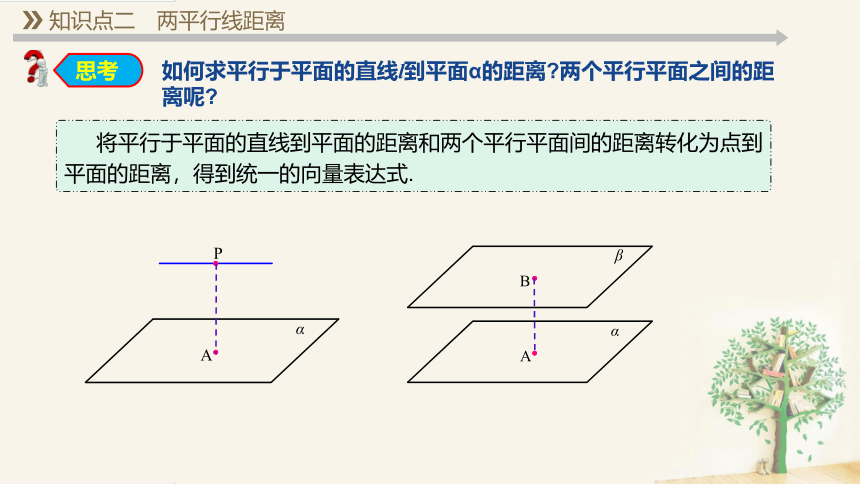
将平行于平面的直线到平面的距离和两个平行平面间的距离转化为点到平面的距离,得到统一的向量表达式.
如何求平行于平面的直线l到平面α的距离 两个平行平面之间的距离呢
例题精讲 ——例1
如图,在棱长为1的正方体ABCD -A1B1C1D1中,E为线段AB1的中点,F为线段AB的中点.
(1)求点B到直线AC1的距离;
(2)求直线FC到平面AEC1的距离.
分析:根据条件建立空间直角坐标系,用坐标表示相关的点、直线的方向向量和平面的法向量,再利用有关公式,通过坐标运算得出相应的距离.
例题精讲 ——例1
如图,在棱长为1的正方体ABCD -A1B1C1D1中,E为线段AB1的中点,F为线段AB的中点.
(1)求点B到直线AC1的距离;
(2)求直线FC到平面AEC1的距离.
解:以D为原点,D1A,D1C1,D1D所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则A(1,0,1),B(1,1,1),C(0,1,1),C(0,1,0),E(1,,0),F(1, ,1),
所以=(0,1,0),=(-1,1,-1),=(0,0,-1),=(-1,1,0),=(-1,2,0),=(0,2,0).
(1)取a==(0,1,0), u==(-1,1,-1),则=1,a
所以,点B到直线AC1的距离为==.
例题精讲 ——例1
如图,在棱长为1的正方体ABCD -A1B1C1D1中,E为线段AB1的中点,F为线段AB的中点.
(1)求点B到直线AC1的距离;
(2)求直线FC到平面AEC1的距离.
解:(2)因为==(-1, ,0),所以FC//EC1,所以FC//平面AEC1.所以点F到平面AEC1的距离即为直线FC到平面AEC1的距离.
设平面AEC1的法向量为n=(x,y,z),则
,所以,
取z=1,则x=1,y=2.
所以,n=(1,2,1)是平面AEC1的一个法向量.
又因为=(0,,0),所以点F到平面AEC1的距离为==
即直线FC到平面AEC1的距离为·
用空间向量研究距离、夹角问题
与用平面向量解决平面几何问题的“三步曲”类似,我们可以得出用空间向量解决立体几何问题的“三步曲”:
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间的距离和夹角等问题;
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;
(3)把向量运算的结果“翻译”成相应的几何结论.
例题精讲 ——变式练习1
(1)在棱长为1的正方体 ABCD -A1B1C1D1中,点A到平面BC1的距离等于________;直线DC到平面AB1的距离等于________;平面DA1到平面CB1的距离等于________.
1
1
1
例题精讲 ——变式练习1
(2)如图,在棱长为1的正方体ABCD -A1B1C1D1中,E为线段 DD1的中点,F为线段BB1的中点
(1)求点A1到直线B1E的距离; (2)求直线FC1,到直线AE的距离;
(3)求点A1到平面AB1E的距离; (4)求直线FC1到平面AB1E的距离.
例题精讲 ——变式练习1
(2)如图,在棱长为1的正方体ABCD -A1B1C1D1中,E为线段 DD1的中点,F为线段BB1的中点
(1)求点A1到直线B1E的距离; (2)求直线FC1,到直线AE的距离;
(3)求点A1到平面AB1E的距离; (4)求直线FC1到平面AB1E的距离.
例题精讲 ——变式练习1
(2)如图,在棱长为1的正方体ABCD -A1B1C1D1中,E为线段 DD1的中点,F为线段BB1的中点
(1)求点A1到直线B1E的距离; (2)求直线FC1,到直线AE的距离;
(3)求点A1到平面AB1E的距离; (4)求直线FC1到平面AB1E的距离.
例题精讲 ——变式练习1
(2)如图,在棱长为1的正方体ABCD -A1B1C1D1中,E为线段 DD1的中点,F为线段BB1的中点
(1)求点A1到直线B1E的距离; (2)求直线FC1,到直线AE的距离;
(3)求点A1到平面AB1E的距离; (4)求直线FC1到平面AB1E的距离.
例题精讲 ——变式练习1
(3) 如图,在棱长为1的正方体ABCD -A1B1C1D1中,求平面A1 DB与平面D1CB的距离.
第一章
1.4.1用空间向量研究直线、平面位置关系
空间中直线、平面的平行
用空间向量研究距离、夹角问题
学习目标
1.能利用投影向量得到点到直线、点到平面的距离公式,
2.结合一些具体的距离问题的解决归纳纳用空间向量解决立体几何问题的“三步曲”.
教学重难点
重点:利用投影向量推导点到直线的距离公式和点到平面的距离公式.
难点:利用投影向量统一研究空间距离问题.
我们知道,立体几何中的距离问题包括点到直线、点到平面、两条平行直线,以及两个平行平面的距离问题等.如何用空间向量解决这些距离问题呢
下面我们先研究用向量方法求直线l外一点P到直线l的距离.
用空间向量研究距离、夹角问题
用空间向量研究距离、夹角问题
知识点一 点到直线的距离
已知直线l的单位方向向量为u,A是直线l上的定点,P是直线l外一点.如何利用这些条件求点P到直线l的距离
探究
如图,向量AP在直线l上的投影向量为,则APQ是直角三角形,因为A,P都是定点,所以||,与u的夹角∠PAQ都是确定的.于是可求||.再利用勾股定理,可以求出点P到直线l的距离PQ.
设=a,则向量在直线l上的投影向量=(au)u.
在RtAPQ中,由勾股定理,得
PQ = =.
知识点二 两平行线距离
思考
两条平行直线,之间的距离,可以转化为直线上任意一点A到直线的距离.
类比点到直线的距离的求法,如何求两条平行直线之间的距离
知识点三 点到平面距离
思考
类比点到直线的距离的求法,如何求平面α外一点P到平面α的距离
第一步
第二步
第三步
第四步
确定平面α的法向量为n
选择“参考向量”
确定“参考向量”向法向量n的投影
求投影向量的模长,得到
PQ=.
知识点二 两平行线距离
思考
将平行于平面的直线到平面的距离和两个平行平面间的距离转化为点到平面的距离,得到统一的向量表达式.
如何求平行于平面的直线l到平面α的距离 两个平行平面之间的距离呢
例题精讲 ——例1
如图,在棱长为1的正方体ABCD -A1B1C1D1中,E为线段AB1的中点,F为线段AB的中点.
(1)求点B到直线AC1的距离;
(2)求直线FC到平面AEC1的距离.
分析:根据条件建立空间直角坐标系,用坐标表示相关的点、直线的方向向量和平面的法向量,再利用有关公式,通过坐标运算得出相应的距离.
例题精讲 ——例1
如图,在棱长为1的正方体ABCD -A1B1C1D1中,E为线段AB1的中点,F为线段AB的中点.
(1)求点B到直线AC1的距离;
(2)求直线FC到平面AEC1的距离.
解:以D为原点,D1A,D1C1,D1D所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则A(1,0,1),B(1,1,1),C(0,1,1),C(0,1,0),E(1,,0),F(1, ,1),
所以=(0,1,0),=(-1,1,-1),=(0,0,-1),=(-1,1,0),=(-1,2,0),=(0,2,0).
(1)取a==(0,1,0), u==(-1,1,-1),则=1,a
所以,点B到直线AC1的距离为==.
例题精讲 ——例1
如图,在棱长为1的正方体ABCD -A1B1C1D1中,E为线段AB1的中点,F为线段AB的中点.
(1)求点B到直线AC1的距离;
(2)求直线FC到平面AEC1的距离.
解:(2)因为==(-1, ,0),所以FC//EC1,所以FC//平面AEC1.所以点F到平面AEC1的距离即为直线FC到平面AEC1的距离.
设平面AEC1的法向量为n=(x,y,z),则
,所以,
取z=1,则x=1,y=2.
所以,n=(1,2,1)是平面AEC1的一个法向量.
又因为=(0,,0),所以点F到平面AEC1的距离为==
即直线FC到平面AEC1的距离为·
用空间向量研究距离、夹角问题
与用平面向量解决平面几何问题的“三步曲”类似,我们可以得出用空间向量解决立体几何问题的“三步曲”:
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间的距离和夹角等问题;
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;
(3)把向量运算的结果“翻译”成相应的几何结论.
例题精讲 ——变式练习1
(1)在棱长为1的正方体 ABCD -A1B1C1D1中,点A到平面BC1的距离等于________;直线DC到平面AB1的距离等于________;平面DA1到平面CB1的距离等于________.
1
1
1
例题精讲 ——变式练习1
(2)如图,在棱长为1的正方体ABCD -A1B1C1D1中,E为线段 DD1的中点,F为线段BB1的中点
(1)求点A1到直线B1E的距离; (2)求直线FC1,到直线AE的距离;
(3)求点A1到平面AB1E的距离; (4)求直线FC1到平面AB1E的距离.
例题精讲 ——变式练习1
(2)如图,在棱长为1的正方体ABCD -A1B1C1D1中,E为线段 DD1的中点,F为线段BB1的中点
(1)求点A1到直线B1E的距离; (2)求直线FC1,到直线AE的距离;
(3)求点A1到平面AB1E的距离; (4)求直线FC1到平面AB1E的距离.
例题精讲 ——变式练习1
(2)如图,在棱长为1的正方体ABCD -A1B1C1D1中,E为线段 DD1的中点,F为线段BB1的中点
(1)求点A1到直线B1E的距离; (2)求直线FC1,到直线AE的距离;
(3)求点A1到平面AB1E的距离; (4)求直线FC1到平面AB1E的距离.
例题精讲 ——变式练习1
(2)如图,在棱长为1的正方体ABCD -A1B1C1D1中,E为线段 DD1的中点,F为线段BB1的中点
(1)求点A1到直线B1E的距离; (2)求直线FC1,到直线AE的距离;
(3)求点A1到平面AB1E的距离; (4)求直线FC1到平面AB1E的距离.
例题精讲 ——变式练习1
(3) 如图,在棱长为1的正方体ABCD -A1B1C1D1中,求平面A1 DB与平面D1CB的距离.
