2013年新疆中考数学回顾与趋势展望
文档属性
| 名称 | 2013年新疆中考数学回顾与趋势展望 |

|
|
| 格式 | zip | ||
| 文件大小 | 374.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 新人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-13 00:00:00 | ||
图片预览









文档简介
课件56张PPT。2013新疆中考数学
回 顾 与 趋 势 展 望 2013年4月1日吴富祖
和田市第五中学中考数学回顾与趋势展望
*中考数学回顾
近几年“内地新疆高中班招生统一考试”数学题目梳理
*2013年新疆数学中考趋势展望
*2013年数学中考复习建议
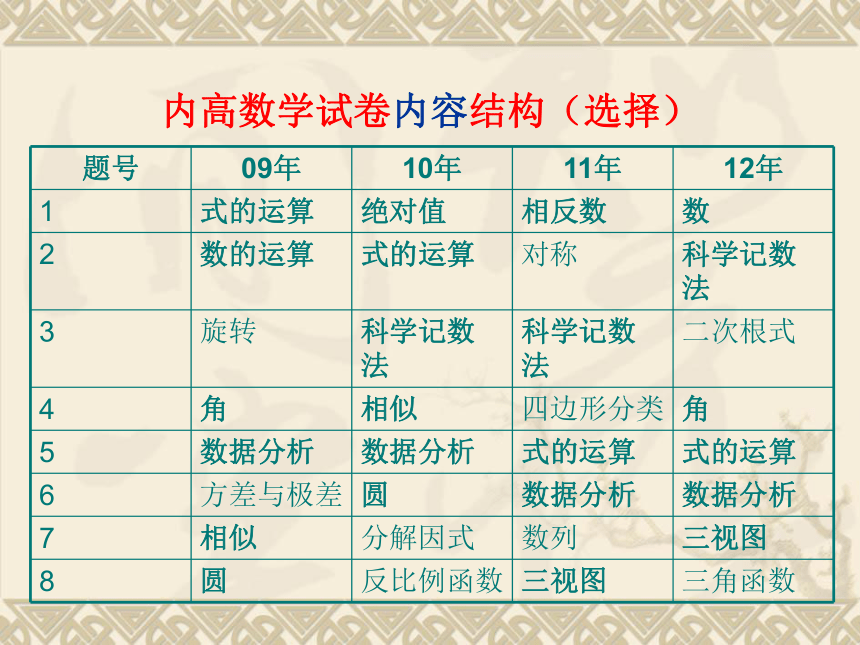
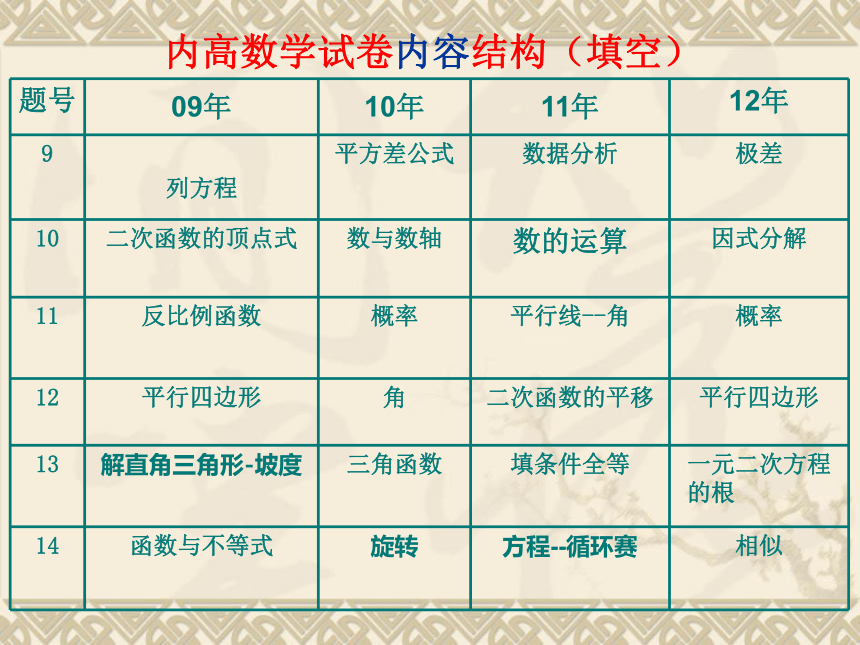
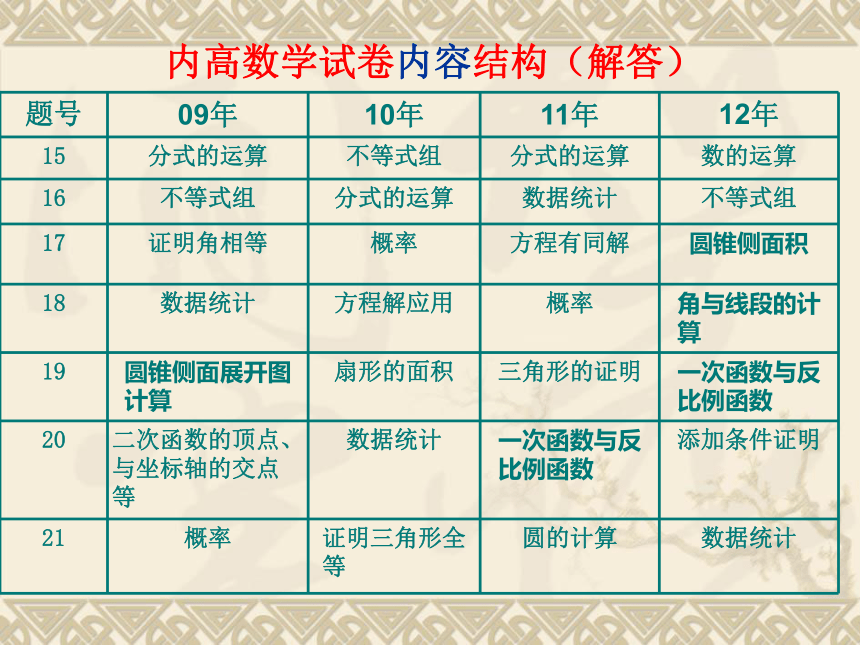
一、近几年“内地新疆高中班招生统一考试”数学题目梳理(一)近几年内高数学试卷内容结构本部分内容以表格的形式呈现,试图从近几年中考数学试题的命制上发现一些规律性的特点,同时发现哪些重要知识点是命题人员重点关注的,进而反复考查的。内高数学试卷内容结构(选择)内高数学试卷内容结构(填空)内高数学试卷内容结构(解答)内高数学试卷内容结构(解答)*下列考点通常在选择填空题中出现 下列考点通常在解答题中出现 (二)2012年内地新疆高中班招生统一考试数学试题分析 ——试题的主要特点1.关注数学核心内容的考查,体现全面性,较好地保证了试卷的效度
2.加强关于空间与图形合理推理能力及综合能力的考查,体现了较好的区分度
3.试卷在充分把握重点的基础上,突出考查数学思想方法与数学探究活动
4.试卷呈现丰富多彩的情境,贴近生活,体现应用性(三)近几年内地新疆高中班招生统一考试 数学试题分析 ——典型题目分析(2012)第14题(5分)如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长为_
分析:根据相似三角形的判定定理求出△ABP∽△PCD,再根据相似三角形
对应边的比等于相似比的平方解答. (2012?新疆)如图,跷跷板AB的一端B碰到地面时,AB与地面的夹角为15°,且OA=OB=3m.
(1)求此时另一端A离地面的距离(精确到0.1m);
(2)若跷动AB,使端点A碰到地面,请画出点A运动的路线(不写画法,保留画图痕迹),并求出点A运动路线的长.
(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)(2012?新疆)如图1,在直角坐标系中,已知△AOC的两个顶点坐标分别为A(2,0),C(0,2). (1)请你以AC的中点为对称中心,画出△AOC的中心对称图形△ABC,此图与原图组成的四边形OABC的形状是 ,请说明理由;(2)如图2,已知D( ,0),过A,C,D的抛物线与(1)所得的四边形OABC的边BC交于点E,求抛物线的解析式及点E的坐标; (3)在问题(2)的图形中,一动点P由抛物线上的点A开始,沿四边形OABC的边从A﹣B﹣C向终点C运动,连接OP交AC于 N,若P运动所经过的路程为x,试问:当x为何值时,△AON为等腰三角形(只写出判断的条件与对应的结果)? 点评: 二次函数综合题.本题综合考查了待定系数法求二次函数解析式、旋转变换作图、正方形、等腰三角形、解一元二次方程等重要知识点.第(3)问是动点型问题,△AON为等腰三角形的情形有三种,注意不要漏解.作为中考压轴题,本题难度不大,有利于基础扎实的考生获得好成绩. 2013年新疆数学中考趋势展望
2013年新疆数学中考趋势展望命题原则:关注《标准》中必须掌握的核心观念和能力;注重进一步学习所必须的数与代数、空间与图形和统计与概率的基础知识和基本技能;注重结果,还要注重过程;既考查思维能力,也考查思维方法;着重考查解决简单的实际问题,还要注意考查创新意识.(考查基础,注重过程,渗透思想,突出能力,强调应用,着意创新 )
核心观念和能力:数感、符号感、空间观念、统计观念、推理能力和应用意识等.
基础知识:概念、法则、性质、公式、公理、定理及由起内容所反映出来的数学思想和方法
基本技能:按一定的程序与步骤计算、作图或画图、进行简单的推理.
几个主要的名词解释思维能力:会观察、实验、比较、猜想、分析、综合、抽象、和概括;会用归纳、演绎和类比进行推理;会合乎逻辑地、准确地阐述自己的思想和观点;会运用数学概念、原理、思想和方法辩明数学关系.
解决简单实际问题的能力:解决带有实际意义的和相关学科中的数学问题,能够解决生产和日常生活中的实际问题;能够使用数学语言表达问题、展开交流.
数学创新意识:对自然界和社会生活中的现象,会从数学角度发现和提出问题,并用数学方法加以探索、研究和解决.
2012年数学中考复习建议 如果七、八年级没有为中招做好充分的准备,那么中招备考复习,时间紧,任务多,压力大,要求“快”字当头。这期间,首先要保持清醒的头脑,随时清楚:我应
该干什么?我在干什么?我应该怎样干?
我离目标更近了,还是过犹不及呢?每一部分复习后我是否反思总结:复习效果怎样?要知道:“没有最好,必须更好”。 第一轮复习
每年的中招试题都没有偏题、怪题,为什么还有那么多同学成绩不理想,连基本题都没有得分呢?
当然是与对知识把握不准确,技能运用不熟练,解题不规范,心态不稳定,没有好的学习习惯,缺乏精益求精、每分必得的勤奋态度有关。 近几年中考中出现的错误举例:
1.不等式﹣2x<4的解集是【 】
(A)x>﹣2 (B)x<﹣2
(C) x>2 (D) x<2
错因: 负迁移,缺乏思维的严谨性,缺乏检验习惯,缺乏警示信号.2. 下列调查适合普查的是 【 】
(A)调查2010年6月份市场上某品牌饮料的质量
(B)了解中央电视台直播北京奥运会开幕式的全国收视率情况
(C) 环保部门调查5月份黄河某段水域的水质量情况
(D)了解全班同学本周末参加社区活动的时间
错因:未形成准确读题的方法、习惯、能力,缺乏检验意识,未能调节好考试状态。3. 16的平方根是 .
错因:基础知识把握不准确,第一轮复习辨析工作不深入、具体,忽视生活思维与数学思维的区别,缺乏进行辨析的意识和习惯,不化简.
4.如图,AB为半圆O的直径,
延长AB到点P,使BP=AB,
PC切半圆O于点C,点D是
弧AC上和点C不重合的一点,则∠D的度数为 .
错因:不熟悉“直径”,“切线”的用法,缺乏“特殊化”的思路和猜想意识,不能顺利进行圆和三角形之间的转化。5.点A(2,1)在反比例函数 的图像上,当1﹤x﹤4时,y的取值范围是 .
错因:缺乏图形结合的思维能力,缺乏特殊化的意识.
6.在一个不透明的袋子中有2个黑球、3个白球,它们除颜色外其他均相同.充分摇匀后,先摸出1个球不放回,再摸出1个球,那么两个球都是黑球的概率为 .
错因:缺乏准确读题的方法、习惯、能力。 解答题
7.先化简,
然后从 中选取一个你认为合适的数作为x的值代入求值.
错因:(1)计算时没有注意符号的确定。
(2)没有注意运算存在的条件。
(3)解答格式不规范.
8.如图,∠BAC=∠ABD,
AC=BD,点O是AD、BC的
交点,点E是AB的中点.试判
断OE和AB的位置关系,并给出证明.错因:
(1)未注意图形中“边、角、边”的关系应该与书写的字母、符号应该是一致的.
(2)未写公共边这个条件.
(3)格式不规范. 没有将对应点的字母写在对应的位置上 . 综上所述 数学中考中部分同学存在的问题1、没有准确把握基本概念、定理或公式的条件和适用范围。缺乏必要的记忆。
2、计算能力弱,影响思维与结果。
3、数学语言素养低,解题格式不规范。
4、只个人的感觉而不善于说理和论证。
5、阅读习惯差、不会审题。复习建议1: 1. 认真体会往年试题的特征.
2. 注意解题规范性.
3. 建立错题档案.
4.每日进行知识和方法的总结.
5. 按考试的要求进行平时的练习.
6.每天进行调节心态的练习.
四“要”
技能要训练
习惯要养成
思维要积极
方法要总结
建议2:四要、四想、三和谐四“想”一想:怎样进行练习?
二想:怎样进行思考?
三想:怎样进行总结?
四想:怎样进行考试? 三“和谐”
严谨与灵活的和谐统一
思维与自动的和谐统一
快速与准确的和谐统一
图形的证明你的脑海中有吗? 第二轮复习——专项突破
从近几年中考看:部分同学的变形、拓展能力欠缺,不善于使用数学思想、方法,缺乏整体思维策略,没有解题思路。
例如不会往“特殊化”和“数学变换”的方向思考,不能联想到“基本图形”。不能有条理地思考。
(原创题:人教版八年级上册第42页探究)如图,要在燃气管道上修建一个泵站,分别向A、B两镇供气,泵站修在管道的什么地方,可使所用的输气管线最短?两定一动型例1.(荆门中考)如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是_______. 2.(呼和浩特中考)如图,已知梯形ABCD,AD∥BC,AD=DC=4,BC=8,点N在BC上,CN=2,E是AB中点,在AC上找一点M使EM+MN的值最小,此时其最小值一定等于【 】
A. 6 B. 8 C. 4 D. 3. 如图,在△ABC中,AC=BC=2,∠ACB=90o,D是BC边的中点,E是AB边上一动点,则EC+ED的最小值是__________.4.(黄石中考)如图,在等腰△ABC中,∠ABC=120O ,点P是底边AC上一个动点,M,N分别是AB,BC的中点,若PM,PN的最小值为2,则△ABC的周长是( )
A.2 B.
C.4 D.5、如图,河岸两侧有、两个村庄,为了村民出行方便,计划在河上修一座桥,桥修在何处才能两村村民来往路程最短?两个定点+两个动点6、(2010?天津)在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点. (1)若E为边OA上的一个动点,当△CDE的周长最小时,求点E的坐标; (2)若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标. 解决此类问题,首先迅速判断“求最小值”的所属问题类型,并立刻联系到该种问题的基本原型。类比基本原型的条件、结论及解决方法来解答该问题。
在学习正方形时,要总结图形的对称性的作用及其图形结构,如“正方形”与“等腰直角三角形”之间建立条件反射;形成完善图形的“补图”意识有利于问题的解答。 一些思维策略、
方法的应用 数学解题不是胡思乱想,要考虑:在具体问题中怎样进行整体思维?发现何时需要分类讨论?怎样进行联想?何时使用逆向思维?怎样进行发散思维?怎样探索隐含条件?怎样简化问题? 常用的解题策略
①综合分析 ②问题转化
③以退为进 ④数形结合
⑤特殊到一般
⑥把问题看作为一个整体
⑦正难则反 ⑧静动结合等等。 典型例举:2013年的中考命题,函数的相关内容将继续是考查的重点,不仅是对函数的基本概念、性质等方面的考查,更要在函数的应用、综合方面加大力度,以体现学数学用数学的新课程理念,因此,对函数的复习应从以下几个方面着手:可从这几方面加以分类综合复习教学:
1) 函数与直线形 直线形包括平行线、相交线、三角形、四边形等内容,解决此类题型的关键是将函数与解直角三角形、相似三角形及特殊的四边形的判定与性质等有关知识相结合,注重点与线、数与形及函数知识之间的转化。
2) 函数与圆 以函数为背景,运用圆的有关性质、定理求直线、抛物线等的解析式,或图象上点的坐标,与圆有关的角的计算等,解决此类题型的关键是将圆的有关性质和函数的图象、性质结合考虑,并注意挖掘题目中的一些隐含条件。
3) 函数与其它几何图形的周长、面积 、 解决此类题型的关键是把图形中相关线段的长用点的坐标表示,并善于将图形面积转化。中考题往往分层设问,前面的问题简单但是为后面的问题提供方法或结论(如归一法)。
往往以平面直角坐标系为联系代数和几何的桥梁;以方程、一次函数、二次函数、三角形和四边形为载体。
解答函数题型需要主动进行探索,需要熟练运用“数形结合”、“分类讨论”等数学思想,需要“以静制动”地研究问题。函数题型的特点:例1:如图,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,其中A(-2,0),B(-1, -3). (1)求出抛物线的解析式 (2)点M为y轴上任意一点,当点M到A、B两点的距离之和为最小时,求此时点M的坐标; (3)在第(2)问的结论下,抛物线上的点P使S△PAD=4S△ABM成立,求点P的坐标.例2:如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D. (1)求该抛物线的解析式与顶点D的坐标; (2)以B、C、D为顶点的三角形是直角三角形吗?为什么? (3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,请指出符合条件的点P的位置,并直接写出点P的坐标;若不存在,请说明理由.例3:如图,二次函数y= ?x2?ax?b的图像与x轴交于A(?,0)、B(2,0)两点,且与y轴交于点C;
(1) 求该拋物线的解析式,并判断△ABC的形状;
(2) 在x轴上方的拋物线上有一点D,且以A、C、D、B四点为顶点的四边形是等腰梯形,请直接写出D点的坐标;
(3) 在此拋物线上是否存在点P,使得以A、C、B、P四点为顶点的四边形是直角梯形?若存在,求出P点的坐标;若不存在,说明理由。例4:平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4), C(2,0)三点. (1)求抛物线的解析式; (2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值. (3)若点P是抛物线上的动点,点Q是直线上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标. 如图,在平面直角坐标系xOy中,我把由两条射线AE,BF和以AB为直径的半圆所组成的图形叫作图形C(注:不含AB线段)。已知A(,),B(,),AE∥BF,且半圆与y轴的交点D在射线AE的反向延长线上。 (1)求两条射线AE,BF所在直线的距离; (2)当一次函数的图象与图形C恰好只有一个公共点时,写出b的取值范围; 当一次函数的图象与图形C恰好只有两个公共点时,写出b的取值范围; (3)已知□AMPQ(四个顶点A,M,P,Q按顺时针方向排列)的各顶点都在图形C上,且不都在两条射线上,求点M的横坐标x的取值范围。对第三轮复习的建议 第三轮复习,以全真练兵为主,要注意对知识掌握的漏洞,对数学思想、方法、解题策略使用的缺乏主动性与不够成熟,对各种题型的不够熟悉,对考试策略(考试心态的调整,解题顺序的确定,解题速度的把握,演草纸的使用,解题后复查的策略)进行考查,及时解决问题。认真归纳知识的遗漏点,分析做错的原因,研究解决的方法。
要把好五关:
1、把好计算的准确关。
2、把好理解审题关。
3、把好表达规范关。
4、把好思维关。
5、把好解题速度关。
6、遇到疑难问题,要“能写即写”。基础为本,能力为魂;
重视过程,重视学生;
关注学情,教学相长;
分类施教,适度提高!我的总复习理念:Thank you再见谢谢倾听,欢迎斧正!
回 顾 与 趋 势 展 望 2013年4月1日吴富祖
和田市第五中学中考数学回顾与趋势展望
*中考数学回顾
近几年“内地新疆高中班招生统一考试”数学题目梳理
*2013年新疆数学中考趋势展望
*2013年数学中考复习建议
一、近几年“内地新疆高中班招生统一考试”数学题目梳理(一)近几年内高数学试卷内容结构本部分内容以表格的形式呈现,试图从近几年中考数学试题的命制上发现一些规律性的特点,同时发现哪些重要知识点是命题人员重点关注的,进而反复考查的。内高数学试卷内容结构(选择)内高数学试卷内容结构(填空)内高数学试卷内容结构(解答)内高数学试卷内容结构(解答)*下列考点通常在选择填空题中出现 下列考点通常在解答题中出现 (二)2012年内地新疆高中班招生统一考试数学试题分析 ——试题的主要特点1.关注数学核心内容的考查,体现全面性,较好地保证了试卷的效度
2.加强关于空间与图形合理推理能力及综合能力的考查,体现了较好的区分度
3.试卷在充分把握重点的基础上,突出考查数学思想方法与数学探究活动
4.试卷呈现丰富多彩的情境,贴近生活,体现应用性(三)近几年内地新疆高中班招生统一考试 数学试题分析 ——典型题目分析(2012)第14题(5分)如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD的长为_
分析:根据相似三角形的判定定理求出△ABP∽△PCD,再根据相似三角形
对应边的比等于相似比的平方解答. (2012?新疆)如图,跷跷板AB的一端B碰到地面时,AB与地面的夹角为15°,且OA=OB=3m.
(1)求此时另一端A离地面的距离(精确到0.1m);
(2)若跷动AB,使端点A碰到地面,请画出点A运动的路线(不写画法,保留画图痕迹),并求出点A运动路线的长.
(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)(2012?新疆)如图1,在直角坐标系中,已知△AOC的两个顶点坐标分别为A(2,0),C(0,2). (1)请你以AC的中点为对称中心,画出△AOC的中心对称图形△ABC,此图与原图组成的四边形OABC的形状是 ,请说明理由;(2)如图2,已知D( ,0),过A,C,D的抛物线与(1)所得的四边形OABC的边BC交于点E,求抛物线的解析式及点E的坐标; (3)在问题(2)的图形中,一动点P由抛物线上的点A开始,沿四边形OABC的边从A﹣B﹣C向终点C运动,连接OP交AC于 N,若P运动所经过的路程为x,试问:当x为何值时,△AON为等腰三角形(只写出判断的条件与对应的结果)? 点评: 二次函数综合题.本题综合考查了待定系数法求二次函数解析式、旋转变换作图、正方形、等腰三角形、解一元二次方程等重要知识点.第(3)问是动点型问题,△AON为等腰三角形的情形有三种,注意不要漏解.作为中考压轴题,本题难度不大,有利于基础扎实的考生获得好成绩. 2013年新疆数学中考趋势展望
2013年新疆数学中考趋势展望命题原则:关注《标准》中必须掌握的核心观念和能力;注重进一步学习所必须的数与代数、空间与图形和统计与概率的基础知识和基本技能;注重结果,还要注重过程;既考查思维能力,也考查思维方法;着重考查解决简单的实际问题,还要注意考查创新意识.(考查基础,注重过程,渗透思想,突出能力,强调应用,着意创新 )
核心观念和能力:数感、符号感、空间观念、统计观念、推理能力和应用意识等.
基础知识:概念、法则、性质、公式、公理、定理及由起内容所反映出来的数学思想和方法
基本技能:按一定的程序与步骤计算、作图或画图、进行简单的推理.
几个主要的名词解释思维能力:会观察、实验、比较、猜想、分析、综合、抽象、和概括;会用归纳、演绎和类比进行推理;会合乎逻辑地、准确地阐述自己的思想和观点;会运用数学概念、原理、思想和方法辩明数学关系.
解决简单实际问题的能力:解决带有实际意义的和相关学科中的数学问题,能够解决生产和日常生活中的实际问题;能够使用数学语言表达问题、展开交流.
数学创新意识:对自然界和社会生活中的现象,会从数学角度发现和提出问题,并用数学方法加以探索、研究和解决.
2012年数学中考复习建议 如果七、八年级没有为中招做好充分的准备,那么中招备考复习,时间紧,任务多,压力大,要求“快”字当头。这期间,首先要保持清醒的头脑,随时清楚:我应
该干什么?我在干什么?我应该怎样干?
我离目标更近了,还是过犹不及呢?每一部分复习后我是否反思总结:复习效果怎样?要知道:“没有最好,必须更好”。 第一轮复习
每年的中招试题都没有偏题、怪题,为什么还有那么多同学成绩不理想,连基本题都没有得分呢?
当然是与对知识把握不准确,技能运用不熟练,解题不规范,心态不稳定,没有好的学习习惯,缺乏精益求精、每分必得的勤奋态度有关。 近几年中考中出现的错误举例:
1.不等式﹣2x<4的解集是【 】
(A)x>﹣2 (B)x<﹣2
(C) x>2 (D) x<2
错因: 负迁移,缺乏思维的严谨性,缺乏检验习惯,缺乏警示信号.2. 下列调查适合普查的是 【 】
(A)调查2010年6月份市场上某品牌饮料的质量
(B)了解中央电视台直播北京奥运会开幕式的全国收视率情况
(C) 环保部门调查5月份黄河某段水域的水质量情况
(D)了解全班同学本周末参加社区活动的时间
错因:未形成准确读题的方法、习惯、能力,缺乏检验意识,未能调节好考试状态。3. 16的平方根是 .
错因:基础知识把握不准确,第一轮复习辨析工作不深入、具体,忽视生活思维与数学思维的区别,缺乏进行辨析的意识和习惯,不化简.
4.如图,AB为半圆O的直径,
延长AB到点P,使BP=AB,
PC切半圆O于点C,点D是
弧AC上和点C不重合的一点,则∠D的度数为 .
错因:不熟悉“直径”,“切线”的用法,缺乏“特殊化”的思路和猜想意识,不能顺利进行圆和三角形之间的转化。5.点A(2,1)在反比例函数 的图像上,当1﹤x﹤4时,y的取值范围是 .
错因:缺乏图形结合的思维能力,缺乏特殊化的意识.
6.在一个不透明的袋子中有2个黑球、3个白球,它们除颜色外其他均相同.充分摇匀后,先摸出1个球不放回,再摸出1个球,那么两个球都是黑球的概率为 .
错因:缺乏准确读题的方法、习惯、能力。 解答题
7.先化简,
然后从 中选取一个你认为合适的数作为x的值代入求值.
错因:(1)计算时没有注意符号的确定。
(2)没有注意运算存在的条件。
(3)解答格式不规范.
8.如图,∠BAC=∠ABD,
AC=BD,点O是AD、BC的
交点,点E是AB的中点.试判
断OE和AB的位置关系,并给出证明.错因:
(1)未注意图形中“边、角、边”的关系应该与书写的字母、符号应该是一致的.
(2)未写公共边这个条件.
(3)格式不规范. 没有将对应点的字母写在对应的位置上 . 综上所述 数学中考中部分同学存在的问题1、没有准确把握基本概念、定理或公式的条件和适用范围。缺乏必要的记忆。
2、计算能力弱,影响思维与结果。
3、数学语言素养低,解题格式不规范。
4、只个人的感觉而不善于说理和论证。
5、阅读习惯差、不会审题。复习建议1: 1. 认真体会往年试题的特征.
2. 注意解题规范性.
3. 建立错题档案.
4.每日进行知识和方法的总结.
5. 按考试的要求进行平时的练习.
6.每天进行调节心态的练习.
四“要”
技能要训练
习惯要养成
思维要积极
方法要总结
建议2:四要、四想、三和谐四“想”一想:怎样进行练习?
二想:怎样进行思考?
三想:怎样进行总结?
四想:怎样进行考试? 三“和谐”
严谨与灵活的和谐统一
思维与自动的和谐统一
快速与准确的和谐统一
图形的证明你的脑海中有吗? 第二轮复习——专项突破
从近几年中考看:部分同学的变形、拓展能力欠缺,不善于使用数学思想、方法,缺乏整体思维策略,没有解题思路。
例如不会往“特殊化”和“数学变换”的方向思考,不能联想到“基本图形”。不能有条理地思考。
(原创题:人教版八年级上册第42页探究)如图,要在燃气管道上修建一个泵站,分别向A、B两镇供气,泵站修在管道的什么地方,可使所用的输气管线最短?两定一动型例1.(荆门中考)如图,菱形ABCD的两条对角线分别长6和8,点P是对角线AC上的一个动点,点M、N分别是边AB、BC的中点,则PM+PN的最小值是_______. 2.(呼和浩特中考)如图,已知梯形ABCD,AD∥BC,AD=DC=4,BC=8,点N在BC上,CN=2,E是AB中点,在AC上找一点M使EM+MN的值最小,此时其最小值一定等于【 】
A. 6 B. 8 C. 4 D. 3. 如图,在△ABC中,AC=BC=2,∠ACB=90o,D是BC边的中点,E是AB边上一动点,则EC+ED的最小值是__________.4.(黄石中考)如图,在等腰△ABC中,∠ABC=120O ,点P是底边AC上一个动点,M,N分别是AB,BC的中点,若PM,PN的最小值为2,则△ABC的周长是( )
A.2 B.
C.4 D.5、如图,河岸两侧有、两个村庄,为了村民出行方便,计划在河上修一座桥,桥修在何处才能两村村民来往路程最短?两个定点+两个动点6、(2010?天津)在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点. (1)若E为边OA上的一个动点,当△CDE的周长最小时,求点E的坐标; (2)若E、F为边OA上的两个动点,且EF=2,当四边形CDEF的周长最小时,求点E、F的坐标. 解决此类问题,首先迅速判断“求最小值”的所属问题类型,并立刻联系到该种问题的基本原型。类比基本原型的条件、结论及解决方法来解答该问题。
在学习正方形时,要总结图形的对称性的作用及其图形结构,如“正方形”与“等腰直角三角形”之间建立条件反射;形成完善图形的“补图”意识有利于问题的解答。 一些思维策略、
方法的应用 数学解题不是胡思乱想,要考虑:在具体问题中怎样进行整体思维?发现何时需要分类讨论?怎样进行联想?何时使用逆向思维?怎样进行发散思维?怎样探索隐含条件?怎样简化问题? 常用的解题策略
①综合分析 ②问题转化
③以退为进 ④数形结合
⑤特殊到一般
⑥把问题看作为一个整体
⑦正难则反 ⑧静动结合等等。 典型例举:2013年的中考命题,函数的相关内容将继续是考查的重点,不仅是对函数的基本概念、性质等方面的考查,更要在函数的应用、综合方面加大力度,以体现学数学用数学的新课程理念,因此,对函数的复习应从以下几个方面着手:可从这几方面加以分类综合复习教学:
1) 函数与直线形 直线形包括平行线、相交线、三角形、四边形等内容,解决此类题型的关键是将函数与解直角三角形、相似三角形及特殊的四边形的判定与性质等有关知识相结合,注重点与线、数与形及函数知识之间的转化。
2) 函数与圆 以函数为背景,运用圆的有关性质、定理求直线、抛物线等的解析式,或图象上点的坐标,与圆有关的角的计算等,解决此类题型的关键是将圆的有关性质和函数的图象、性质结合考虑,并注意挖掘题目中的一些隐含条件。
3) 函数与其它几何图形的周长、面积 、 解决此类题型的关键是把图形中相关线段的长用点的坐标表示,并善于将图形面积转化。中考题往往分层设问,前面的问题简单但是为后面的问题提供方法或结论(如归一法)。
往往以平面直角坐标系为联系代数和几何的桥梁;以方程、一次函数、二次函数、三角形和四边形为载体。
解答函数题型需要主动进行探索,需要熟练运用“数形结合”、“分类讨论”等数学思想,需要“以静制动”地研究问题。函数题型的特点:例1:如图,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,其中A(-2,0),B(-1, -3). (1)求出抛物线的解析式 (2)点M为y轴上任意一点,当点M到A、B两点的距离之和为最小时,求此时点M的坐标; (3)在第(2)问的结论下,抛物线上的点P使S△PAD=4S△ABM成立,求点P的坐标.例2:如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D. (1)求该抛物线的解析式与顶点D的坐标; (2)以B、C、D为顶点的三角形是直角三角形吗?为什么? (3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,请指出符合条件的点P的位置,并直接写出点P的坐标;若不存在,请说明理由.例3:如图,二次函数y= ?x2?ax?b的图像与x轴交于A(?,0)、B(2,0)两点,且与y轴交于点C;
(1) 求该拋物线的解析式,并判断△ABC的形状;
(2) 在x轴上方的拋物线上有一点D,且以A、C、D、B四点为顶点的四边形是等腰梯形,请直接写出D点的坐标;
(3) 在此拋物线上是否存在点P,使得以A、C、B、P四点为顶点的四边形是直角梯形?若存在,求出P点的坐标;若不存在,说明理由。例4:平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4), C(2,0)三点. (1)求抛物线的解析式; (2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值. (3)若点P是抛物线上的动点,点Q是直线上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标. 如图,在平面直角坐标系xOy中,我把由两条射线AE,BF和以AB为直径的半圆所组成的图形叫作图形C(注:不含AB线段)。已知A(,),B(,),AE∥BF,且半圆与y轴的交点D在射线AE的反向延长线上。 (1)求两条射线AE,BF所在直线的距离; (2)当一次函数的图象与图形C恰好只有一个公共点时,写出b的取值范围; 当一次函数的图象与图形C恰好只有两个公共点时,写出b的取值范围; (3)已知□AMPQ(四个顶点A,M,P,Q按顺时针方向排列)的各顶点都在图形C上,且不都在两条射线上,求点M的横坐标x的取值范围。对第三轮复习的建议 第三轮复习,以全真练兵为主,要注意对知识掌握的漏洞,对数学思想、方法、解题策略使用的缺乏主动性与不够成熟,对各种题型的不够熟悉,对考试策略(考试心态的调整,解题顺序的确定,解题速度的把握,演草纸的使用,解题后复查的策略)进行考查,及时解决问题。认真归纳知识的遗漏点,分析做错的原因,研究解决的方法。
要把好五关:
1、把好计算的准确关。
2、把好理解审题关。
3、把好表达规范关。
4、把好思维关。
5、把好解题速度关。
6、遇到疑难问题,要“能写即写”。基础为本,能力为魂;
重视过程,重视学生;
关注学情,教学相长;
分类施教,适度提高!我的总复习理念:Thank you再见谢谢倾听,欢迎斧正!
同课章节目录
