1_5_1 平面上两点间的距离(共17张PPT)
文档属性
| 名称 | 1_5_1 平面上两点间的距离(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 688.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 22:16:51 | ||
图片预览





文档简介
(共17张PPT)
1.5 平面上的距离
1.5.1 平面上两点间的距离
学习目标
1.掌握平面上两点间的距离公式、中点坐标公式.
2.能运用距离公式、中点坐标公式解决一些简单的问题.
3.理解坐标法的意义,并会用坐标法研究问题.
1 |两点间的距离
1.公式
平面上P1(x1,y1),P2(x2,y2)两点间的距离公式P1P2=① .
2.特殊情况
当直线P1P2垂直于y轴时,P1P2=|x2-x1|;当直线P1P2垂直于x轴时,P1P2=|y2-y1|;当点P1,P2
中有一个是原点时,P1P2= (或 ).
2 |中点坐标公式
1.公式
对于平面上两点P1(x1,y1),P2(x2,y2),线段P1P2的中点是M(x0,y0),则② .
2.中点坐标公式的推导
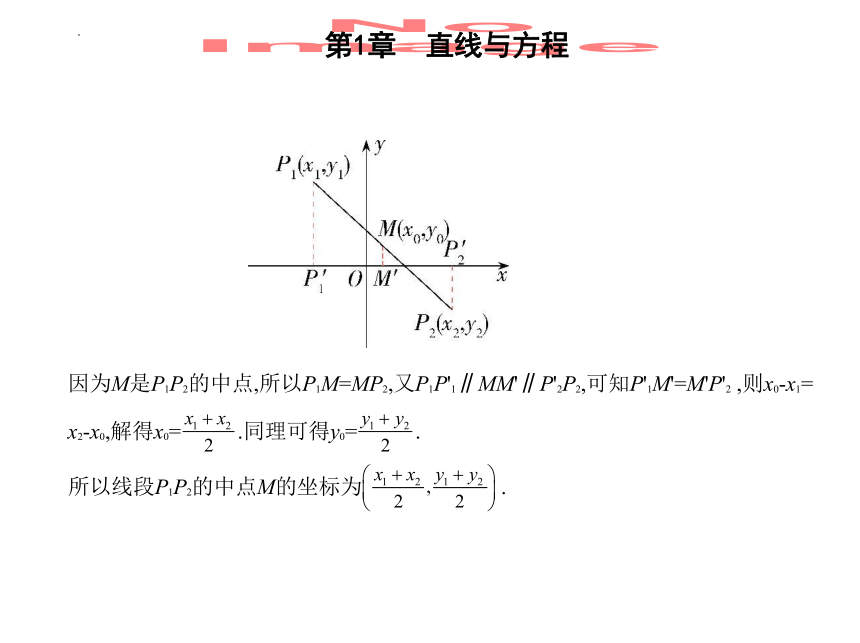
对于平面上的两点P1(x1,y1),P2(x2,y2),线段P1P2的中点是M(x0,y0).如图,过点P1,M,P2向
x轴作垂线,垂足分别为P'1,M',P'2,则P'1,M',P'2的横坐标分别为x1,x0,x2.
因为M是P1P2的中点,所以P1M=MP2,又P1P'1∥MM'∥P'2P2,可知P'1M'=M'P'2 ,则x0-x1=
x2-x0,解得x0= .同理可得y0= .
所以线段P1P2的中点M的坐标为 .
判断正误,正确的画“√”,错误的画“ ”.
1.P1(0,a),P2(0,b)两点间的距离为a-b. ( )
提示:P1(0,a),P2(0,b)两点间的距离应该为|a-b|.
2.已知平面内的两点A(x1,y1),B(x2,y2),直线AB的斜率为k,则直线上A,B两点间的距
离AB= ·|x1-x2|. ( √ )
提示:AB=
= = ·|x1-x2|,
即AB= ·|x1-x2|.
3.已知点A(-2,-1),B(a,3),且AB=5,则a的值为1. ( )
提示: 由题意知AB= =5,解得a=1或-5.
4.已知A(4,0),B(0,4),从点P(1,0)射出的光线被直线AB反射后,再射到直线OB上,最
后经OB反射后回到P点,则光线所经过的路程是 . ( √ )
提示:点P关于y轴的对称点P'的坐标是(-1,0),设点P关于直线AB:x+y-4=0的对称点
为P″(a,b),
∴ 解得 ∴P″(4,3),
∴光线所经过的路程P'P″= = .
1 |常见的对称问题
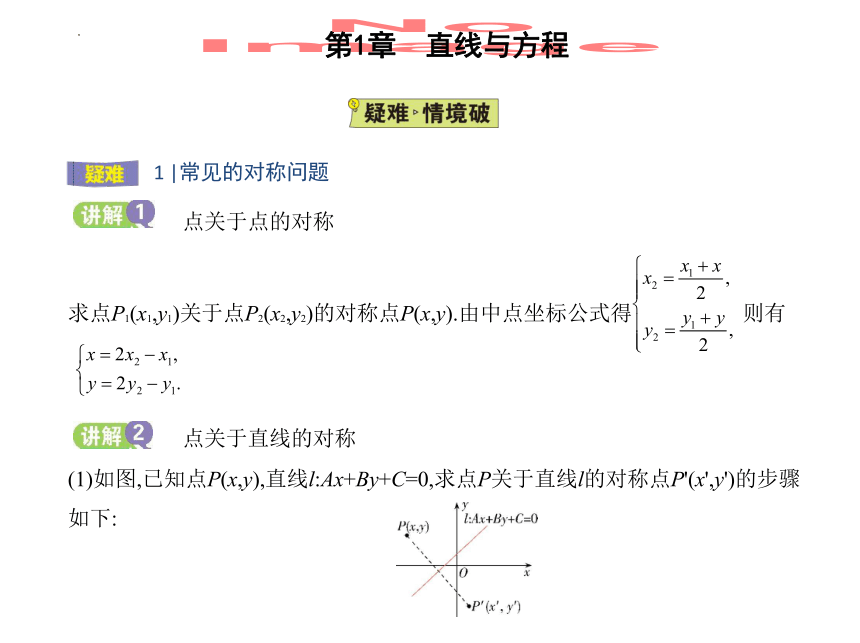
点关于点的对称
求点P1(x1,y1)关于点P2(x2,y2)的对称点P(x,y).由中点坐标公式得 则有
点关于直线的对称
(1)如图,已知点P(x,y),直线l:Ax+By+C=0,求点P关于直线l的对称点P'(x',y')的步骤
如下:
第一步,直线PP'和l垂直,故kPP'·kl=-1①.
第二步,PP'的中点在直线l上,即点 满足直线方程Ax+By+C=0,
得到A· +B· +C=0②.
第三步,联立①②两式可以解出x',y'.
(2)点关于直线对称的常用结论:
①点P(x0,y0)关于x轴的对称点P'(x0,-y0);
②点P(x0,y0)关于y轴的对称点P'(-x0,y0);
③点P(x0,y0)关于直线y=x的对称点P'(y0,x0);
④点P(x0,y0)关于直线y=-x的对称点P'(-y0,-x0);
⑤点P(x0,y0)关于直线x=m(m≠0)的对称点P'(2m-x0,y0);
⑥点P(x0,y0)关于直线y=n(n≠0)的对称点P'(x0,2n-y0).
直线关于点的对称
直线关于点的对称实际上可以转化为点关于点的对称.
直线关于直线的对称
已知直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,求直线l1关于直线l2的对称直线的方程.
如果l1∥l2,则设所求直线的方程为A1x+B1y+m=0(m≠C1),然后在l1上找一点P,求出
点P关于直线l2的对称点P'(x',y'),再代入A1x+B1y+m=0,即可解出m.
如果l1与l2相交,则先找出l1与l2的交点P,然后在l1上确定一点M(不同于交点),找出
这一点关于l2的对称点M',由两点即可确定所求直线的方程.
已知直线l:x+2y-2=0,试求:
(1)点P(-2,-1)关于直线l的对称点的坐标;
(2)直线l1:y=x-2关于直线l对称的直线l2的方程;
(3)直线l关于点A(1,1)对称的直线方程.
解析 (1)设点P(-2,-1)关于直线l的对称点为P'(x0,y0),
则线段PP'的中点M在直线l上,且PP'⊥l.
所以有 解得
故P'点的坐标为 .
(2)解法一:由 得直线l与l1的交点为N(2,0),在l1上任取一点B(0,-2),设B
关于直线l的对称点为B'(x1,y1),
则
解得 即B' ,
所以直线l2的斜率为kNB'= =7,
所以l2的方程为y=7(x-2),即7x-y-14=0.
解法二:由于直线l1:y=x-2关于直线l对称的直线为l2,则l2上任一点P1(x,y)关于l的对
称点P'1(x',y')一定在直线l1上.
由 得
把(x',y')代入方程y=x-2并整理得7x-y-14=0,
故l2的方程为7x-y-14=0.
(3)设直线l关于点A(1,1)对称的直线为l',则直线l'上任一点P'2(x'2,y'2)关于点A的对
称点P2(x2,y2)一定在直线l上.
由 得
将(x2,y2)代入直线l的方程得x'2+2y'2-4=0,所以直线l'的方程为x+2y-4=0.
方法技巧 关于对称问题,要充分利用“垂直平分”这个基本条件,“垂直”是
指两个对称点的连线与已知直线垂直,“平分”是指两个对称点连成的线段的中
点在已知直线上,可通过这两个条件列方程组求解.
2 |对称在求最值中的应用
在直线l上求一点P,使P到两个定点的距离之和最小的求法
(1)当两定点A、B在直线l的异侧时,如图①,连接AB,线段AB交直线l于点P,此
时AB与l的交点P到两定点的距离之和最小,最小值为AB的长.在直线l上任取一点
P',则P'A+P'B≥AB.
(2)当两定点A、B在直线l的同侧时,如图②,作点A关于直线l的对称点A',连接A'B
交直线l于点P,此时点P到两定点A,B的距离之和最小.
在直线l上求一点P,使P到两定点的距离之差的绝对值最大的求法
(1)当两定点A、B在直线l的同侧时(A、B连线与l不平行),连接BA并延长,交直线l
于点P.此时点P到两定点的距离之差的绝对值最大,最大值为AB的长.如图③,在l
上任意取一点P',则有|P'B-P'A|≤AB=|PB-PA|.
(2)当两定点A、B在直线l的异侧时,作点A关于直线l的对称点A',连接BA'并延长,
交l于点P.此时点P到两定点距离之差的绝对值最大,最大值为|PB-PA|=|PB-PA'|=
A'B.如图④,在l上任取一点P',则有|P'B-P'A|=|P'B-P'A'|≤A'B.
已知直线l:x-2y+8=0和两点A(2,0),B(-2,-4),且点P在直线l上.
(1)当PA+PB最小时,点P的坐标为 ;
(2)当|PB-PA|最大时,点P的坐标为 .
思路点拨
(1)利用对称性将直线同侧两点转化为异侧两点,利用两点之间线段最短求最小
值,进而得出点P的坐标.
(2)A、B两点在直线l的同侧,根据三角形两边之差小于第三边,得出当A,B,P三点
共线时,|PB-PA|取得最大值,进而得出点P的坐标.
解析 (1)设点A关于直线l的对称点为A'(m,n),
则
解得 故A'(-2,8).
因为P为直线l上一点,所以PA+PB=PA'+PB≥A'B,当且仅当B,P,A'三点共线时,PA+
PB取得最小值,最小值为A'B的长,此时点P为直线A'B与直线l的交点.又直线A'B的
方程为x=-2,所以由 得 故点P的坐标为(-2,3).
(2)A、B两点在直线l的同侧,P是直线l上一点,则|PB-PA|≤AB,当且仅当A,B,P三点
共线时,|PB-PA|取得最大值,最大值为AB的长,此时点P为直线AB与直线l的交点.
又直线AB的方程为y=x-2,所以由 得 故点P的坐标为(12,10).
答案 (1)(-2,3) (2)(12,10)
1.5 平面上的距离
1.5.1 平面上两点间的距离
学习目标
1.掌握平面上两点间的距离公式、中点坐标公式.
2.能运用距离公式、中点坐标公式解决一些简单的问题.
3.理解坐标法的意义,并会用坐标法研究问题.
1 |两点间的距离
1.公式
平面上P1(x1,y1),P2(x2,y2)两点间的距离公式P1P2=① .
2.特殊情况
当直线P1P2垂直于y轴时,P1P2=|x2-x1|;当直线P1P2垂直于x轴时,P1P2=|y2-y1|;当点P1,P2
中有一个是原点时,P1P2= (或 ).
2 |中点坐标公式
1.公式
对于平面上两点P1(x1,y1),P2(x2,y2),线段P1P2的中点是M(x0,y0),则② .
2.中点坐标公式的推导
对于平面上的两点P1(x1,y1),P2(x2,y2),线段P1P2的中点是M(x0,y0).如图,过点P1,M,P2向
x轴作垂线,垂足分别为P'1,M',P'2,则P'1,M',P'2的横坐标分别为x1,x0,x2.
因为M是P1P2的中点,所以P1M=MP2,又P1P'1∥MM'∥P'2P2,可知P'1M'=M'P'2 ,则x0-x1=
x2-x0,解得x0= .同理可得y0= .
所以线段P1P2的中点M的坐标为 .
判断正误,正确的画“√”,错误的画“ ”.
1.P1(0,a),P2(0,b)两点间的距离为a-b. ( )
提示:P1(0,a),P2(0,b)两点间的距离应该为|a-b|.
2.已知平面内的两点A(x1,y1),B(x2,y2),直线AB的斜率为k,则直线上A,B两点间的距
离AB= ·|x1-x2|. ( √ )
提示:AB=
= = ·|x1-x2|,
即AB= ·|x1-x2|.
3.已知点A(-2,-1),B(a,3),且AB=5,则a的值为1. ( )
提示: 由题意知AB= =5,解得a=1或-5.
4.已知A(4,0),B(0,4),从点P(1,0)射出的光线被直线AB反射后,再射到直线OB上,最
后经OB反射后回到P点,则光线所经过的路程是 . ( √ )
提示:点P关于y轴的对称点P'的坐标是(-1,0),设点P关于直线AB:x+y-4=0的对称点
为P″(a,b),
∴ 解得 ∴P″(4,3),
∴光线所经过的路程P'P″= = .
1 |常见的对称问题
点关于点的对称
求点P1(x1,y1)关于点P2(x2,y2)的对称点P(x,y).由中点坐标公式得 则有
点关于直线的对称
(1)如图,已知点P(x,y),直线l:Ax+By+C=0,求点P关于直线l的对称点P'(x',y')的步骤
如下:
第一步,直线PP'和l垂直,故kPP'·kl=-1①.
第二步,PP'的中点在直线l上,即点 满足直线方程Ax+By+C=0,
得到A· +B· +C=0②.
第三步,联立①②两式可以解出x',y'.
(2)点关于直线对称的常用结论:
①点P(x0,y0)关于x轴的对称点P'(x0,-y0);
②点P(x0,y0)关于y轴的对称点P'(-x0,y0);
③点P(x0,y0)关于直线y=x的对称点P'(y0,x0);
④点P(x0,y0)关于直线y=-x的对称点P'(-y0,-x0);
⑤点P(x0,y0)关于直线x=m(m≠0)的对称点P'(2m-x0,y0);
⑥点P(x0,y0)关于直线y=n(n≠0)的对称点P'(x0,2n-y0).
直线关于点的对称
直线关于点的对称实际上可以转化为点关于点的对称.
直线关于直线的对称
已知直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,求直线l1关于直线l2的对称直线的方程.
如果l1∥l2,则设所求直线的方程为A1x+B1y+m=0(m≠C1),然后在l1上找一点P,求出
点P关于直线l2的对称点P'(x',y'),再代入A1x+B1y+m=0,即可解出m.
如果l1与l2相交,则先找出l1与l2的交点P,然后在l1上确定一点M(不同于交点),找出
这一点关于l2的对称点M',由两点即可确定所求直线的方程.
已知直线l:x+2y-2=0,试求:
(1)点P(-2,-1)关于直线l的对称点的坐标;
(2)直线l1:y=x-2关于直线l对称的直线l2的方程;
(3)直线l关于点A(1,1)对称的直线方程.
解析 (1)设点P(-2,-1)关于直线l的对称点为P'(x0,y0),
则线段PP'的中点M在直线l上,且PP'⊥l.
所以有 解得
故P'点的坐标为 .
(2)解法一:由 得直线l与l1的交点为N(2,0),在l1上任取一点B(0,-2),设B
关于直线l的对称点为B'(x1,y1),
则
解得 即B' ,
所以直线l2的斜率为kNB'= =7,
所以l2的方程为y=7(x-2),即7x-y-14=0.
解法二:由于直线l1:y=x-2关于直线l对称的直线为l2,则l2上任一点P1(x,y)关于l的对
称点P'1(x',y')一定在直线l1上.
由 得
把(x',y')代入方程y=x-2并整理得7x-y-14=0,
故l2的方程为7x-y-14=0.
(3)设直线l关于点A(1,1)对称的直线为l',则直线l'上任一点P'2(x'2,y'2)关于点A的对
称点P2(x2,y2)一定在直线l上.
由 得
将(x2,y2)代入直线l的方程得x'2+2y'2-4=0,所以直线l'的方程为x+2y-4=0.
方法技巧 关于对称问题,要充分利用“垂直平分”这个基本条件,“垂直”是
指两个对称点的连线与已知直线垂直,“平分”是指两个对称点连成的线段的中
点在已知直线上,可通过这两个条件列方程组求解.
2 |对称在求最值中的应用
在直线l上求一点P,使P到两个定点的距离之和最小的求法
(1)当两定点A、B在直线l的异侧时,如图①,连接AB,线段AB交直线l于点P,此
时AB与l的交点P到两定点的距离之和最小,最小值为AB的长.在直线l上任取一点
P',则P'A+P'B≥AB.
(2)当两定点A、B在直线l的同侧时,如图②,作点A关于直线l的对称点A',连接A'B
交直线l于点P,此时点P到两定点A,B的距离之和最小.
在直线l上求一点P,使P到两定点的距离之差的绝对值最大的求法
(1)当两定点A、B在直线l的同侧时(A、B连线与l不平行),连接BA并延长,交直线l
于点P.此时点P到两定点的距离之差的绝对值最大,最大值为AB的长.如图③,在l
上任意取一点P',则有|P'B-P'A|≤AB=|PB-PA|.
(2)当两定点A、B在直线l的异侧时,作点A关于直线l的对称点A',连接BA'并延长,
交l于点P.此时点P到两定点距离之差的绝对值最大,最大值为|PB-PA|=|PB-PA'|=
A'B.如图④,在l上任取一点P',则有|P'B-P'A|=|P'B-P'A'|≤A'B.
已知直线l:x-2y+8=0和两点A(2,0),B(-2,-4),且点P在直线l上.
(1)当PA+PB最小时,点P的坐标为 ;
(2)当|PB-PA|最大时,点P的坐标为 .
思路点拨
(1)利用对称性将直线同侧两点转化为异侧两点,利用两点之间线段最短求最小
值,进而得出点P的坐标.
(2)A、B两点在直线l的同侧,根据三角形两边之差小于第三边,得出当A,B,P三点
共线时,|PB-PA|取得最大值,进而得出点P的坐标.
解析 (1)设点A关于直线l的对称点为A'(m,n),
则
解得 故A'(-2,8).
因为P为直线l上一点,所以PA+PB=PA'+PB≥A'B,当且仅当B,P,A'三点共线时,PA+
PB取得最小值,最小值为A'B的长,此时点P为直线A'B与直线l的交点.又直线A'B的
方程为x=-2,所以由 得 故点P的坐标为(-2,3).
(2)A、B两点在直线l的同侧,P是直线l上一点,则|PB-PA|≤AB,当且仅当A,B,P三点
共线时,|PB-PA|取得最大值,最大值为AB的长,此时点P为直线AB与直线l的交点.
又直线AB的方程为y=x-2,所以由 得 故点P的坐标为(12,10).
答案 (1)(-2,3) (2)(12,10)
