1.1.2 空间向量的数量积运算 课件(共16张PPT)
文档属性
| 名称 | 1.1.2 空间向量的数量积运算 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 483.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
1.1.2 空间向量的数量积运算
1.掌握空间向量的夹角及其表示方法.
2.掌握空间向量的数量积及其运算律.
3.能用空间向量的数量积解决立体几何问题.
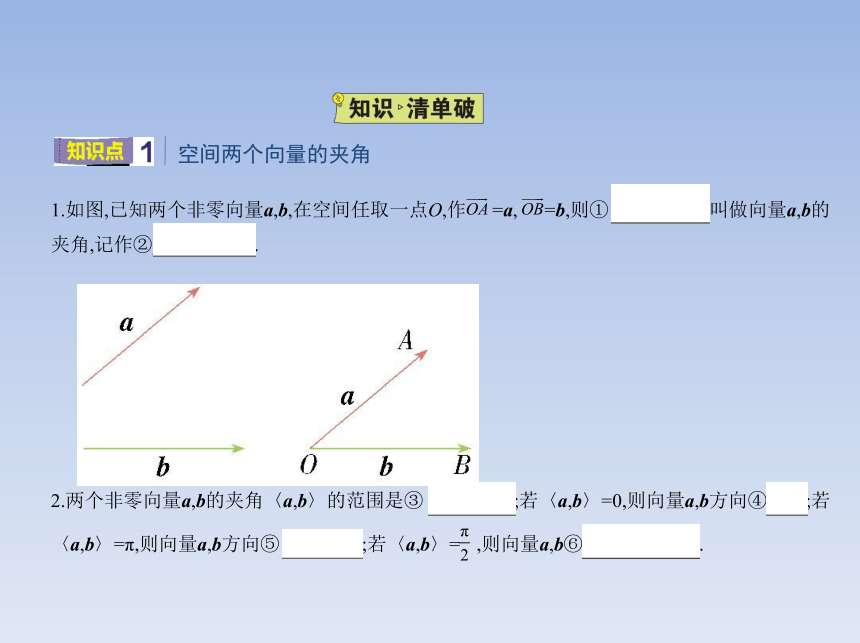
1.如图,已知两个非零向量a,b,在空间任取一点O,作 =a, =b,则① ∠AOB 叫做向量a,b的夹角,记作② 〈a,b〉 .
2.两个非零向量a,b的夹角〈a,b〉的范围是③ [0,π] ;若〈a,b〉=0,则向量a,b方向④相同;若〈a,b〉=π,则向量a,b方向⑤ 相反 ;若〈a,b〉= ,则向量a,b⑥ 互相垂直 .
空间两个向量的夹角
1.定义
已知两个非零向量a,b,则⑦ |a||b|cos〈a,b〉 叫做a,b的数量积,记作⑧ a·b .
即a·b=|a||b|cos〈a,b〉.
规定:零向量与任意向量的数量积为⑨ 0 .
2.运算律
(1)(λa)·b=⑩ λ(a·b) ,λ∈R;
(2)交换律:a·b= b·a ;
(3)分配律:a·(b+c)= a·b+a·c .
空间向量的数量积
1.a·e= |a|cos〈a,e〉 (其中e为单位向量);
2.若a,b为非零向量,则a⊥b a·b=0 ;
3.a·a=|a||a|cos〈a,a〉=|a|2或|a|= = ;
4.若a,b为非零向量,则cos〈a,b〉= ;
5.|a·b|≤|a||b|(当且仅当a,b共线时,等号成立).
空间向量数量积的性质
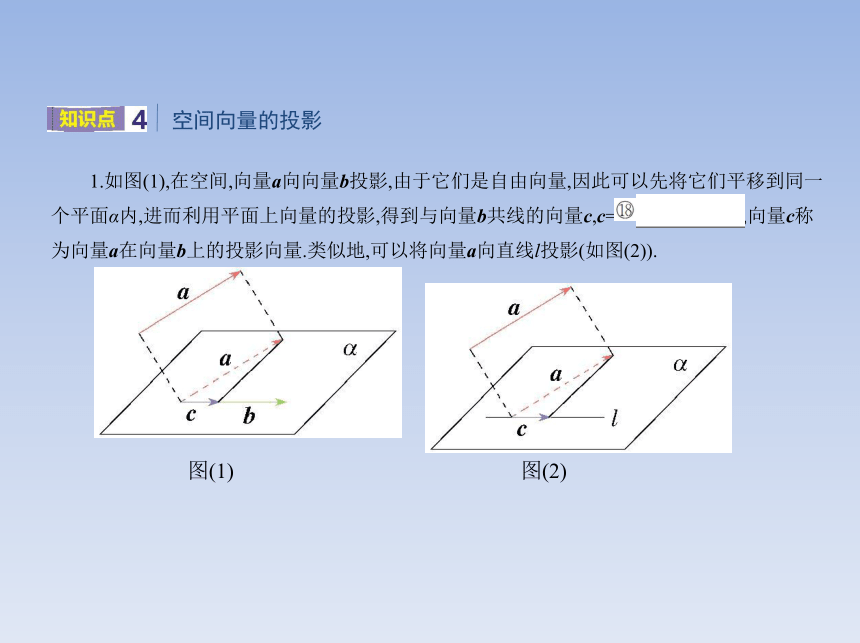
1.如图(1),在空间,向量a向向量b投影,由于它们是自由向量,因此可以先将它们平移到同一个平面α内,进而利用平面上向量的投影,得到与向量b共线的向量c,c= ,向量c称为向量a在向量b上的投影向量.类似地,可以将向量a向直线l投影(如图(2)).
图(1) 图(2)
空间向量的投影
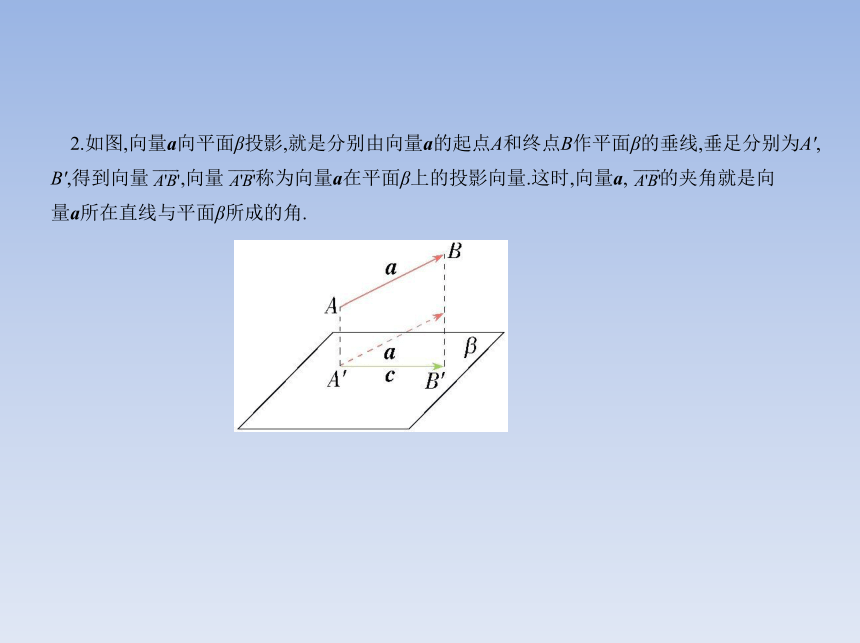
2.如图,向量a向平面β投影,就是分别由向量a的起点A和终点B作平面β的垂线,垂足分别为A',
B',得到向量 ,向量 称为向量a在平面β上的投影向量.这时,向量a, 的夹角就是向
量a所在直线与平面β所成的角.
1.对于非零向量a,b,〈a,b〉与〈a,-b〉相等. ( )
提示:〈a,b〉与〈a,-b〉互补.
2.对于任意向量a,b,c,都有(a·b)c=a(b·c). ( )
提示:(a·b)c与c共线,a(b·c)与a共线,但c与a不一定共线.
3.若a·b=b·c,且b≠0,则a=c. ( )
提示:由a·b=b·c知b·(a-c)=0,即b与a-c垂直或a=c,故a=c不一定成立.
4.若a·b=0,则a=0或b=0. ( )
判断正误,正确的画“ √” ,错误的画“ ”.
空间向量的数量积运算
1.空间向量运算的两种方法
(1)利用定义:利用a·b=|a||b|cos〈a,b〉并结合运算律进行计算.
(2)利用图形:计算两个向量的数量积,可先将各向量移到同一顶点,利用图形寻找夹角,再代
入数量积公式进行运算.
2.在几何体中求空间向量的数量积的步骤
(1)将各向量分解成已知模和夹角的向量的组合形式.
(2)利用向量的运算律将数量积展开,转化为已知模和夹角的向量的数量积.
(3)代入向量的数量积公式进行运算求解.
(1)已知空间四边形ABCD的每条边和对角线的长都等于a,点E,F分别是BC,AD的中点,则
· = ;
(2)在四面体OABC中,棱OA,OB,OC两两垂直,且OA=1,OB=2,OC=3,G为△ABC的重心,则 ·
( + + )= .
解析 (1) · = ( + )· = ( · + · )= (a2cos 60°+a2cos 60°)= a2.
(2)由题意知 = + = + × ( + )= + [( - )+( - )]= + +
,
∴ ·( + + )= ·( + + )= + + = ×22+ ×32+
×12= .
答案 (1) a2 (2)
利用空间向量的数量积求夹角
1.求空间两个向量的夹角的方法
(1)结合图形,平移向量,利用空间向量的夹角定义来求,但要注意向量夹角的范围;
(2)先求a·b,再利用公式cos〈a,b〉= 求cos〈a,b〉,最后确定〈a,b〉.
2.求两条异面直线所成的角的步骤
(1)根据题设条件在所求的异面直线上取两个向量(即直线的方向向量);
(2)将异面直线所成角的问题转化为向量夹角问题;
(3)利用向量的数量积求向量夹角的余弦值;
(4)异面直线所成的角为锐角或直角,利用向量的数量积求向量夹角的余弦值应将余弦值加
上绝对值,进而求出异面直线所成的角的大小.
3.由于向量的夹角的取值范围为[0,π],而异面直线所成的角的取值范围为 ,因此利用向
量的数量积求异面直线所成的角时,要注意角度之间的关系,当〈a,b〉∈ 时,它们相等;
当〈a,b〉∈ 时,它们互补.
利用空间向量的数量积求距离(或线段长)
1.用数量积求两点间距离的步骤
(1)用向量的模表示此距离;
(2)用已知模和夹角的向量表示此向量;
(3)用公式a·a=|a|2求|a|;
(4)|a|即为所求距离.
2.求模公式的推广
由公式|a|= 可以推广为|a±b|= = .
已知线段AB在平面α内,线段AC⊥α,线段BD⊥AB,且与α所成的角是30°,如果AB=a,AC=BD=
b,求C,D间的距离.
思路点拨
已知线段AB、AC、BD的长度,由已知可得线段AB、AC、BD两两所成角,所以用 + +
表示 ,结合向量的数量积公式求出C,D间的距离.
解析 由AC⊥α,知AC⊥AB.如图,过点D作DD'⊥α于点D',连接BD',则∠DBD'=30°,〈 , 〉
=120°,
所以| |2= · =( + + )2=| |2+| |2+| |2+2 · +2 · +2 · =b2+a2+b2
+2b2cos 120°=a2+b2,故CD= .
利用空间向量的数量积证明垂直
利用空间向量的数量积判断或证明线线、线面垂直的思路
(1)由数量积的性质a⊥b a·b=0可知,要证两直线垂直,可构造与两直线分别平行的向量,只
要证明这两个向量的数量积为0即可.
(2)用向量法证明线面垂直,离不开线面垂直的判定定理,需将线面垂直转化为线线垂直,然
后利用向量法证明线线垂直即可.
用向量法证明垂直关系的步骤:
①把几何问题转化为向量问题;
②用已知向量表示所证向量;
③结合数量积公式和运算律证数量积为0;
④将向量问题回归到几何问题.
如图,正四面体VABC的高VD的中点为O,VC的中点为M.求证:AO,BO,CO两两垂直.
思路点拨
因为正四面体各条棱都相等,且相邻两条棱的夹角为60°,所以可以用过同一顶点的三条棱表示AO,BO,CO,利用数量积的运算证明垂直.
证明 设 =a, =b, =c,正四面体的棱长为1,
则 = (a+b+c),
= (b+c-5a),
= (a+c-5b),
= (a+b-5c),
所以 · = (b+c-5a)·(a+c-5b)= (18a·b-9|a|2)= ×(18×1×1×cos 60°-9)=0,
所以 ⊥ ,即AO⊥BO.
同理,AO⊥CO,BO⊥CO.
所以AO,BO,CO两两垂直.
1.1.2 空间向量的数量积运算
1.掌握空间向量的夹角及其表示方法.
2.掌握空间向量的数量积及其运算律.
3.能用空间向量的数量积解决立体几何问题.
1.如图,已知两个非零向量a,b,在空间任取一点O,作 =a, =b,则① ∠AOB 叫做向量a,b的夹角,记作② 〈a,b〉 .
2.两个非零向量a,b的夹角〈a,b〉的范围是③ [0,π] ;若〈a,b〉=0,则向量a,b方向④相同;若〈a,b〉=π,则向量a,b方向⑤ 相反 ;若〈a,b〉= ,则向量a,b⑥ 互相垂直 .
空间两个向量的夹角
1.定义
已知两个非零向量a,b,则⑦ |a||b|cos〈a,b〉 叫做a,b的数量积,记作⑧ a·b .
即a·b=|a||b|cos〈a,b〉.
规定:零向量与任意向量的数量积为⑨ 0 .
2.运算律
(1)(λa)·b=⑩ λ(a·b) ,λ∈R;
(2)交换律:a·b= b·a ;
(3)分配律:a·(b+c)= a·b+a·c .
空间向量的数量积
1.a·e= |a|cos〈a,e〉 (其中e为单位向量);
2.若a,b为非零向量,则a⊥b a·b=0 ;
3.a·a=|a||a|cos〈a,a〉=|a|2或|a|= = ;
4.若a,b为非零向量,则cos〈a,b〉= ;
5.|a·b|≤|a||b|(当且仅当a,b共线时,等号成立).
空间向量数量积的性质
1.如图(1),在空间,向量a向向量b投影,由于它们是自由向量,因此可以先将它们平移到同一个平面α内,进而利用平面上向量的投影,得到与向量b共线的向量c,c= ,向量c称为向量a在向量b上的投影向量.类似地,可以将向量a向直线l投影(如图(2)).
图(1) 图(2)
空间向量的投影
2.如图,向量a向平面β投影,就是分别由向量a的起点A和终点B作平面β的垂线,垂足分别为A',
B',得到向量 ,向量 称为向量a在平面β上的投影向量.这时,向量a, 的夹角就是向
量a所在直线与平面β所成的角.
1.对于非零向量a,b,〈a,b〉与〈a,-b〉相等. ( )
提示:〈a,b〉与〈a,-b〉互补.
2.对于任意向量a,b,c,都有(a·b)c=a(b·c). ( )
提示:(a·b)c与c共线,a(b·c)与a共线,但c与a不一定共线.
3.若a·b=b·c,且b≠0,则a=c. ( )
提示:由a·b=b·c知b·(a-c)=0,即b与a-c垂直或a=c,故a=c不一定成立.
4.若a·b=0,则a=0或b=0. ( )
判断正误,正确的画“ √” ,错误的画“ ”.
空间向量的数量积运算
1.空间向量运算的两种方法
(1)利用定义:利用a·b=|a||b|cos〈a,b〉并结合运算律进行计算.
(2)利用图形:计算两个向量的数量积,可先将各向量移到同一顶点,利用图形寻找夹角,再代
入数量积公式进行运算.
2.在几何体中求空间向量的数量积的步骤
(1)将各向量分解成已知模和夹角的向量的组合形式.
(2)利用向量的运算律将数量积展开,转化为已知模和夹角的向量的数量积.
(3)代入向量的数量积公式进行运算求解.
(1)已知空间四边形ABCD的每条边和对角线的长都等于a,点E,F分别是BC,AD的中点,则
· = ;
(2)在四面体OABC中,棱OA,OB,OC两两垂直,且OA=1,OB=2,OC=3,G为△ABC的重心,则 ·
( + + )= .
解析 (1) · = ( + )· = ( · + · )= (a2cos 60°+a2cos 60°)= a2.
(2)由题意知 = + = + × ( + )= + [( - )+( - )]= + +
,
∴ ·( + + )= ·( + + )= + + = ×22+ ×32+
×12= .
答案 (1) a2 (2)
利用空间向量的数量积求夹角
1.求空间两个向量的夹角的方法
(1)结合图形,平移向量,利用空间向量的夹角定义来求,但要注意向量夹角的范围;
(2)先求a·b,再利用公式cos〈a,b〉= 求cos〈a,b〉,最后确定〈a,b〉.
2.求两条异面直线所成的角的步骤
(1)根据题设条件在所求的异面直线上取两个向量(即直线的方向向量);
(2)将异面直线所成角的问题转化为向量夹角问题;
(3)利用向量的数量积求向量夹角的余弦值;
(4)异面直线所成的角为锐角或直角,利用向量的数量积求向量夹角的余弦值应将余弦值加
上绝对值,进而求出异面直线所成的角的大小.
3.由于向量的夹角的取值范围为[0,π],而异面直线所成的角的取值范围为 ,因此利用向
量的数量积求异面直线所成的角时,要注意角度之间的关系,当〈a,b〉∈ 时,它们相等;
当〈a,b〉∈ 时,它们互补.
利用空间向量的数量积求距离(或线段长)
1.用数量积求两点间距离的步骤
(1)用向量的模表示此距离;
(2)用已知模和夹角的向量表示此向量;
(3)用公式a·a=|a|2求|a|;
(4)|a|即为所求距离.
2.求模公式的推广
由公式|a|= 可以推广为|a±b|= = .
已知线段AB在平面α内,线段AC⊥α,线段BD⊥AB,且与α所成的角是30°,如果AB=a,AC=BD=
b,求C,D间的距离.
思路点拨
已知线段AB、AC、BD的长度,由已知可得线段AB、AC、BD两两所成角,所以用 + +
表示 ,结合向量的数量积公式求出C,D间的距离.
解析 由AC⊥α,知AC⊥AB.如图,过点D作DD'⊥α于点D',连接BD',则∠DBD'=30°,〈 , 〉
=120°,
所以| |2= · =( + + )2=| |2+| |2+| |2+2 · +2 · +2 · =b2+a2+b2
+2b2cos 120°=a2+b2,故CD= .
利用空间向量的数量积证明垂直
利用空间向量的数量积判断或证明线线、线面垂直的思路
(1)由数量积的性质a⊥b a·b=0可知,要证两直线垂直,可构造与两直线分别平行的向量,只
要证明这两个向量的数量积为0即可.
(2)用向量法证明线面垂直,离不开线面垂直的判定定理,需将线面垂直转化为线线垂直,然
后利用向量法证明线线垂直即可.
用向量法证明垂直关系的步骤:
①把几何问题转化为向量问题;
②用已知向量表示所证向量;
③结合数量积公式和运算律证数量积为0;
④将向量问题回归到几何问题.
如图,正四面体VABC的高VD的中点为O,VC的中点为M.求证:AO,BO,CO两两垂直.
思路点拨
因为正四面体各条棱都相等,且相邻两条棱的夹角为60°,所以可以用过同一顶点的三条棱表示AO,BO,CO,利用数量积的运算证明垂直.
证明 设 =a, =b, =c,正四面体的棱长为1,
则 = (a+b+c),
= (b+c-5a),
= (a+c-5b),
= (a+b-5c),
所以 · = (b+c-5a)·(a+c-5b)= (18a·b-9|a|2)= ×(18×1×1×cos 60°-9)=0,
所以 ⊥ ,即AO⊥BO.
同理,AO⊥CO,BO⊥CO.
所以AO,BO,CO两两垂直.
