湘教版七年级上册1.6 有理数的乘方课件(共17张PPT)
文档属性
| 名称 | 湘教版七年级上册1.6 有理数的乘方课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 223.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 07:05:02 | ||
图片预览


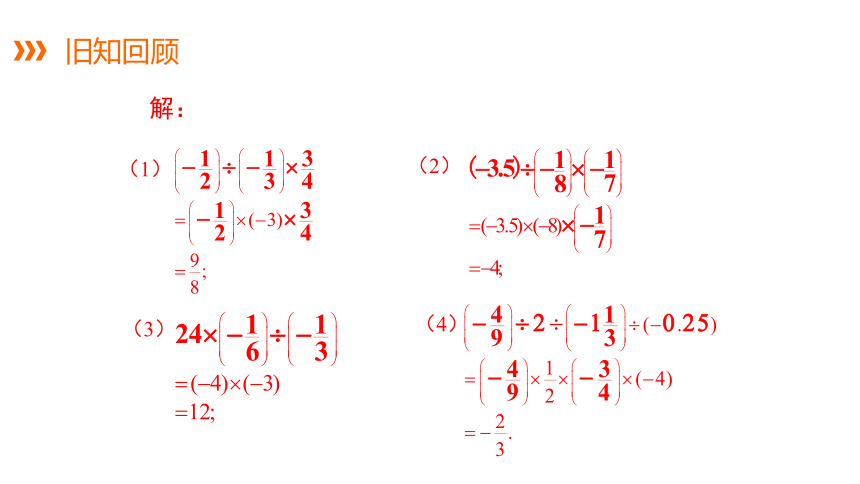


文档简介
(共17张PPT)
第1章 有理数
1.6 第1课时 有理数的乘方
计算:
(1) ;
(2) ;
(3) ;
(4) .
旧知回顾
解:
(1)
(2)
(3)
(4)
旧知回顾
动脑筋
(-2)×(-2)×(-2)×(-2)×(-2)可以简记为什么?
在小学我们就学过,2×2可以简记为22,2×2×2可以简记为23,那么2×2×2×2可以简记为24;2×2×2×2×2可以简记为25.
类似地,
(-2)×(-2)可以简记为_______ ;
(-2)×(-2)×(-2)可以简记为_______;
(-2)×(-2)×(-2)×(-2)可以简记为_______;
(-2)×(-2)×(-2)×(-2)×(-2)可以简记为______.
(-2)2
(-2)3
(-2)4
(-2)5
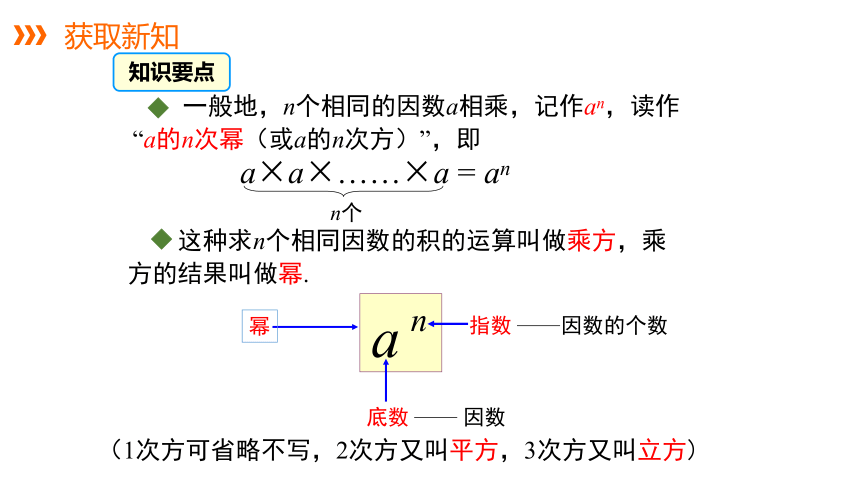
获取新知
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
(1次方可省略不写,2次方又叫平方,3次方又叫立方)
a×a×……×a = an
n个
幂
指数
因数的个数
底数
因数
一般地,n个相同的因数a相乘,记作an,读作“a的n次幂(或a的n次方)”,即
知识要点
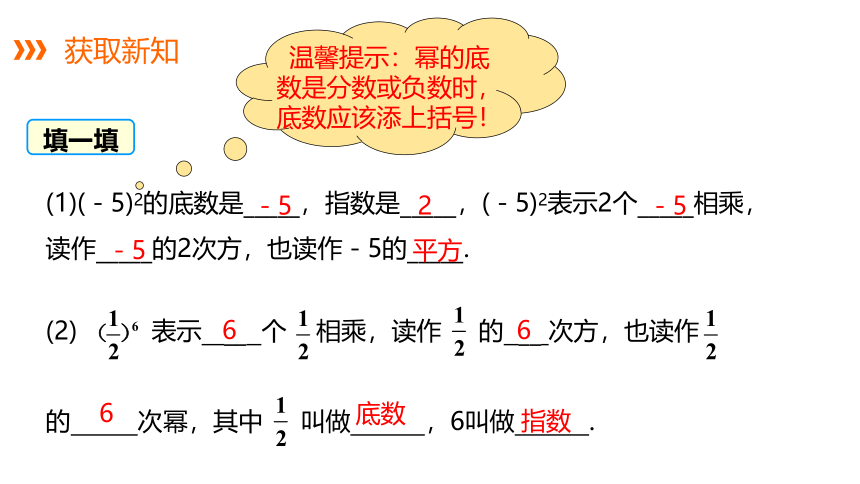
获取新知
(1)(-5)2的底数是_____,指数是_____,(-5)2表示2个_____相乘,读作_____的2次方,也读作-5的_____.
(2) 表示 __ 个 相乘,读作 的 __ 次方,也读作 的 次幂,其中 叫做 ,6叫做 .
温馨提示:幂的底数是分数或负数时,底数应该添上括号!
填一填
-5
2
-5
-5
平方
6
6
6
底数
指数
获取新知
议一议
(-2)4与-24 的含义相同吗?它们的结果一样吗?(-3)2与-32的含义与结果也分别相同吗?
(-2)4与表示-2的4次方。
-24 表示2的4次方的相反数。
......
获取新知
(-4)2 -42
有括号
无括号
-4的平方
4的平方的相反数
2个(-4)相乘
即(-4)×(-4)
2个4相乘的积的相反数
即-(4×4)
-16
写法
读法
意义
结果
16
注意:底数是负数或分数时,必须加上括号.
获取新知
(-3)2 -32
有括号
无括号
-3的平方
3的平方的相反数
2个(-3)相乘
即(-3)×(-3)
2个3相乘的积的相反数
即-(3×3)
-9
写法
读法
意义
结果
9
注意:底数是负数或分数时,必须加上括号.
获取新知
计算
(1) (-3)3 (2) 07
(3) (4)
解: (1) (-3)3 =(-3)×(-3)×(-3)=-27
(2) 07 =0×0×0×0 ×0×0×0=0
(3) = × × =
(4) = × × × =
例1
注意:在书写负数、分数的乘方时,一定要把整个负数、分数用括号括起来.
例题讲解
完成下面的内容,寻找规律:
(1)22=___,23= ___ ,24= ___ ,25= ___;
(2)(-2)2= ___ ,(-2)3= ___ ,
(-2)4= ___,(-2)5= _____ ;
(3)(-1)1= ___ ,(-1)3= ___ ,
(-1)4= ___ ,(-1)5= ___ ;
(4)02= ___ ,03= ___ ,
04= ___ ,05= ___ .
32
4
4
8
16
-8
16
-32
1
1
-1
-1
0
0
0
0
随堂演练
说一说
正数的任何正整数次幂都是什么数?负数的奇次幂是什么数?负数的偶次是什么数?0的任何正整数次幂是什么?
正数的任何正整数次幂都是正数;负数的奇次幂都是负数,负数的偶次幂都是正数;0的任何正整数次幂都是0
获取新知
快速计算下面几道题:
(1)13 (2)12018 (3)(-1)8
(4)(-1)2018 (5)(-1)7 (6)(-1)2017
议一议
=1
=1
=1
=1
=-1
=-1
思考:你发现了什么规律呢?
获取新知
(1)1的任何正整数次幂都为1;
(2)-1的幂很有规律:
-1的奇次幂是-1, -1的偶次幂是1.
注意:当底数是负数或分数时,底数一定要加上括弧,这也是辨认底数的方法.
规 律
获取新知
(1) (2)
解:
计算
例2
例题讲解
计算:
(2)-23×(-2)2.
解:原式=-8×4=-32.
随堂演练
1.求几个相同因数的积的运算,叫做乘方.
2.乘方的符号法则:
(1)正数的任何次幂都是正数;
(2)负数的奇次幂是负数,负数的偶次幂是正数;
(3)零的正数次幂都是零.
幂
指数
底数
课堂小结
第1章 有理数
1.6 第1课时 有理数的乘方
计算:
(1) ;
(2) ;
(3) ;
(4) .
旧知回顾
解:
(1)
(2)
(3)
(4)
旧知回顾
动脑筋
(-2)×(-2)×(-2)×(-2)×(-2)可以简记为什么?
在小学我们就学过,2×2可以简记为22,2×2×2可以简记为23,那么2×2×2×2可以简记为24;2×2×2×2×2可以简记为25.
类似地,
(-2)×(-2)可以简记为_______ ;
(-2)×(-2)×(-2)可以简记为_______;
(-2)×(-2)×(-2)×(-2)可以简记为_______;
(-2)×(-2)×(-2)×(-2)×(-2)可以简记为______.
(-2)2
(-2)3
(-2)4
(-2)5
获取新知
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
(1次方可省略不写,2次方又叫平方,3次方又叫立方)
a×a×……×a = an
n个
幂
指数
因数的个数
底数
因数
一般地,n个相同的因数a相乘,记作an,读作“a的n次幂(或a的n次方)”,即
知识要点
获取新知
(1)(-5)2的底数是_____,指数是_____,(-5)2表示2个_____相乘,读作_____的2次方,也读作-5的_____.
(2) 表示 __ 个 相乘,读作 的 __ 次方,也读作 的 次幂,其中 叫做 ,6叫做 .
温馨提示:幂的底数是分数或负数时,底数应该添上括号!
填一填
-5
2
-5
-5
平方
6
6
6
底数
指数
获取新知
议一议
(-2)4与-24 的含义相同吗?它们的结果一样吗?(-3)2与-32的含义与结果也分别相同吗?
(-2)4与表示-2的4次方。
-24 表示2的4次方的相反数。
......
获取新知
(-4)2 -42
有括号
无括号
-4的平方
4的平方的相反数
2个(-4)相乘
即(-4)×(-4)
2个4相乘的积的相反数
即-(4×4)
-16
写法
读法
意义
结果
16
注意:底数是负数或分数时,必须加上括号.
获取新知
(-3)2 -32
有括号
无括号
-3的平方
3的平方的相反数
2个(-3)相乘
即(-3)×(-3)
2个3相乘的积的相反数
即-(3×3)
-9
写法
读法
意义
结果
9
注意:底数是负数或分数时,必须加上括号.
获取新知
计算
(1) (-3)3 (2) 07
(3) (4)
解: (1) (-3)3 =(-3)×(-3)×(-3)=-27
(2) 07 =0×0×0×0 ×0×0×0=0
(3) = × × =
(4) = × × × =
例1
注意:在书写负数、分数的乘方时,一定要把整个负数、分数用括号括起来.
例题讲解
完成下面的内容,寻找规律:
(1)22=___,23= ___ ,24= ___ ,25= ___;
(2)(-2)2= ___ ,(-2)3= ___ ,
(-2)4= ___,(-2)5= _____ ;
(3)(-1)1= ___ ,(-1)3= ___ ,
(-1)4= ___ ,(-1)5= ___ ;
(4)02= ___ ,03= ___ ,
04= ___ ,05= ___ .
32
4
4
8
16
-8
16
-32
1
1
-1
-1
0
0
0
0
随堂演练
说一说
正数的任何正整数次幂都是什么数?负数的奇次幂是什么数?负数的偶次是什么数?0的任何正整数次幂是什么?
正数的任何正整数次幂都是正数;负数的奇次幂都是负数,负数的偶次幂都是正数;0的任何正整数次幂都是0
获取新知
快速计算下面几道题:
(1)13 (2)12018 (3)(-1)8
(4)(-1)2018 (5)(-1)7 (6)(-1)2017
议一议
=1
=1
=1
=1
=-1
=-1
思考:你发现了什么规律呢?
获取新知
(1)1的任何正整数次幂都为1;
(2)-1的幂很有规律:
-1的奇次幂是-1, -1的偶次幂是1.
注意:当底数是负数或分数时,底数一定要加上括弧,这也是辨认底数的方法.
规 律
获取新知
(1) (2)
解:
计算
例2
例题讲解
计算:
(2)-23×(-2)2.
解:原式=-8×4=-32.
随堂演练
1.求几个相同因数的积的运算,叫做乘方.
2.乘方的符号法则:
(1)正数的任何次幂都是正数;
(2)负数的奇次幂是负数,负数的偶次幂是正数;
(3)零的正数次幂都是零.
幂
指数
底数
课堂小结
同课章节目录
