湘教版数学七年级上册同步课件:2.5 第3课时 整式的加法和减法(14张ppt)
文档属性
| 名称 | 湘教版数学七年级上册同步课件:2.5 第3课时 整式的加法和减法(14张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 260.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
第2章 代数式
2.5 第3课时 整式的加法和减法
1、化简m-n-(m+n)的结果是( )
A.0 B.2m C.-2n D.2m-2n
2、化简4x-4-(4x-5)=________.
3、化简2(2x-5)-3(1-4x)=________.
4、三角形的第一边长是(2a+b)cm,第二边长是2(a+b)cm,第三边长比第二边长短b cm,则这个三角形的周长是________cm.
C
1
16x-13
(6a+4b)
旧知回顾
5、化简下列各式:
(1)8m+2n+(5m-n); (2)(5p-3q)-3( ).
解:
旧知回顾
动脑筋
有两个大小不一的长方体纸盒,已知小长方体纸盒的长、宽、高分别是x、y、z,且大长方体纸盒的体积是小长方体纸盒体积的24倍.
x
y
z
(1)这两个纸盒的体积和为多少?
(2)大纸盒与小纸盒的体积差为多少?
情景引入
小纸盒和大纸盒的体积分别是xyz和24xyz,故两纸盒的体积和为xyz+24xyz=25xyz
大纸盒的体积与小纸盒的体积差为24xyz-xyz=23xyz.
获取新知
解:根据题意,得
例4 求多项式 与多项式 的和与差.
去括号
合并同类项
去括号
合并同类项
例题讲解
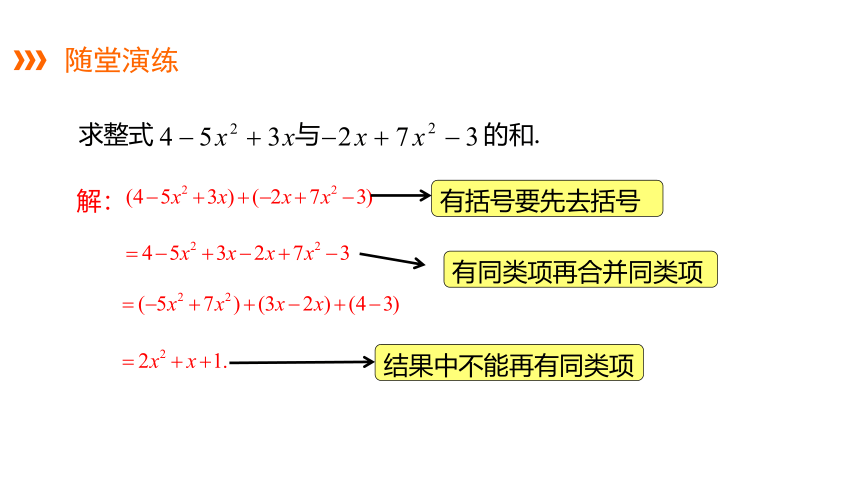
求整式 与 的和.
解:
有括号要先去括号
有同类项再合并同类项
结果中不能再有同类项
随堂演练
整式化简求值的一般步骤:
(1)化简:去括号→合并同类项;
(2)代入求值:格式:“当……时,原式=……”.
先化简, 再求值.
5xy -(4x2 + 2xy)-2(2.5xy +10),其中x=1,y =-2.
解 5xy-(4x2+2xy)-2(2.5xy+10)
= 5xy-4x2-2xy-(5xy+20)
= 5xy-4x2-2xy-5xy-20
= -4x2-2xy-20.
当 x=1 ,y= -2 时,
-4x2-2xy-20= -4×12-2×1×(-2)-20= -20 .
例5
例题讲解
例4 如图,正方形的边长为x,用整式表示图中阴影部分的面积,并计算当x=4m时阴影部分的面积( 取3.14).
x
x
解:阴影部分的面积为:
当x=4m 时,阴影部分的面积为:
例题讲解
1、化简求值.
2(a2-ab)-3(2a2-ab),其中a=-2,b=3;
解:原式=-4a2+ab,
当a=-2,b=3时,
原式=-4×(-2)2+(-2)×3=-22;
2、已知a-b=2,ab=-1,
求(4a-5b-ab)-(2a-3b+5ab)的值.
解:原式=2(a-b)-6ab,
∵a-b=2,ab=-1.
∴原式=2×2-6×(-1)=10.
随堂演练
3、 一种笔记本的单价是x元,圆珠笔的单价是y元.小红买这种笔记本3本,买圆珠笔2支;小明买这种笔记本4本,买圆珠笔3支.买这些笔记本和圆珠笔,小红和小明一共花费多少钱?
解:小红买笔记本和圆珠笔共花费(3x+2y)元,小明买笔记本和圆珠笔共花费(4x+3y)元.
小红和小明一共花费(单位:元)
(3x+2y)+(4x+3y)
=3x+2y+4x+3y
=7x+5y
你还能有其他解法吗?
随堂演练
另解:小红和小明买笔记本共花费(3x+4x)元,买圆珠笔共花费(2y+3y)元.
小红和小明一共花费(单位:元)
(3x+4x)+(2y+3y)
=7x+5y
分别计算笔记本和圆珠的花费.
随堂演练
整式加减的步骤
整式加减的应用
整式的加减
去括号
合并同类项
课堂小结
第2章 代数式
2.5 第3课时 整式的加法和减法
1、化简m-n-(m+n)的结果是( )
A.0 B.2m C.-2n D.2m-2n
2、化简4x-4-(4x-5)=________.
3、化简2(2x-5)-3(1-4x)=________.
4、三角形的第一边长是(2a+b)cm,第二边长是2(a+b)cm,第三边长比第二边长短b cm,则这个三角形的周长是________cm.
C
1
16x-13
(6a+4b)
旧知回顾
5、化简下列各式:
(1)8m+2n+(5m-n); (2)(5p-3q)-3( ).
解:
旧知回顾
动脑筋
有两个大小不一的长方体纸盒,已知小长方体纸盒的长、宽、高分别是x、y、z,且大长方体纸盒的体积是小长方体纸盒体积的24倍.
x
y
z
(1)这两个纸盒的体积和为多少?
(2)大纸盒与小纸盒的体积差为多少?
情景引入
小纸盒和大纸盒的体积分别是xyz和24xyz,故两纸盒的体积和为xyz+24xyz=25xyz
大纸盒的体积与小纸盒的体积差为24xyz-xyz=23xyz.
获取新知
解:根据题意,得
例4 求多项式 与多项式 的和与差.
去括号
合并同类项
去括号
合并同类项
例题讲解
求整式 与 的和.
解:
有括号要先去括号
有同类项再合并同类项
结果中不能再有同类项
随堂演练
整式化简求值的一般步骤:
(1)化简:去括号→合并同类项;
(2)代入求值:格式:“当……时,原式=……”.
先化简, 再求值.
5xy -(4x2 + 2xy)-2(2.5xy +10),其中x=1,y =-2.
解 5xy-(4x2+2xy)-2(2.5xy+10)
= 5xy-4x2-2xy-(5xy+20)
= 5xy-4x2-2xy-5xy-20
= -4x2-2xy-20.
当 x=1 ,y= -2 时,
-4x2-2xy-20= -4×12-2×1×(-2)-20= -20 .
例5
例题讲解
例4 如图,正方形的边长为x,用整式表示图中阴影部分的面积,并计算当x=4m时阴影部分的面积( 取3.14).
x
x
解:阴影部分的面积为:
当x=4m 时,阴影部分的面积为:
例题讲解
1、化简求值.
2(a2-ab)-3(2a2-ab),其中a=-2,b=3;
解:原式=-4a2+ab,
当a=-2,b=3时,
原式=-4×(-2)2+(-2)×3=-22;
2、已知a-b=2,ab=-1,
求(4a-5b-ab)-(2a-3b+5ab)的值.
解:原式=2(a-b)-6ab,
∵a-b=2,ab=-1.
∴原式=2×2-6×(-1)=10.
随堂演练
3、 一种笔记本的单价是x元,圆珠笔的单价是y元.小红买这种笔记本3本,买圆珠笔2支;小明买这种笔记本4本,买圆珠笔3支.买这些笔记本和圆珠笔,小红和小明一共花费多少钱?
解:小红买笔记本和圆珠笔共花费(3x+2y)元,小明买笔记本和圆珠笔共花费(4x+3y)元.
小红和小明一共花费(单位:元)
(3x+2y)+(4x+3y)
=3x+2y+4x+3y
=7x+5y
你还能有其他解法吗?
随堂演练
另解:小红和小明买笔记本共花费(3x+4x)元,买圆珠笔共花费(2y+3y)元.
小红和小明一共花费(单位:元)
(3x+4x)+(2y+3y)
=7x+5y
分别计算笔记本和圆珠的花费.
随堂演练
整式加减的步骤
整式加减的应用
整式的加减
去括号
合并同类项
课堂小结
同课章节目录
