湘教版数学七年级上册同步课件:2.5 第1课时 合并同类项(共17张PPT)
文档属性
| 名称 | 湘教版数学七年级上册同步课件:2.5 第1课时 合并同类项(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 371.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
第2章 代数式
2.5 第1课时 合并同类项
单项式:由数与字母的积组成的代数式。(单独的数和字母也是单项式);
系数:单项式中,与字母相乘的数;
次数:一个单项式中,所有字母的指数的和;
多项式:由几个单项式的和组成的代数式;
项:组成多项式的没和单项式;
常数项:不含字母的项
旧知回顾
1.单项式-3a2bc的系数是______,次数是____.
2.多项式3x2y-xy3+y2- 的次数是_____,常数项是_____,.
-3
4
4
旧知回顾
动脑筋
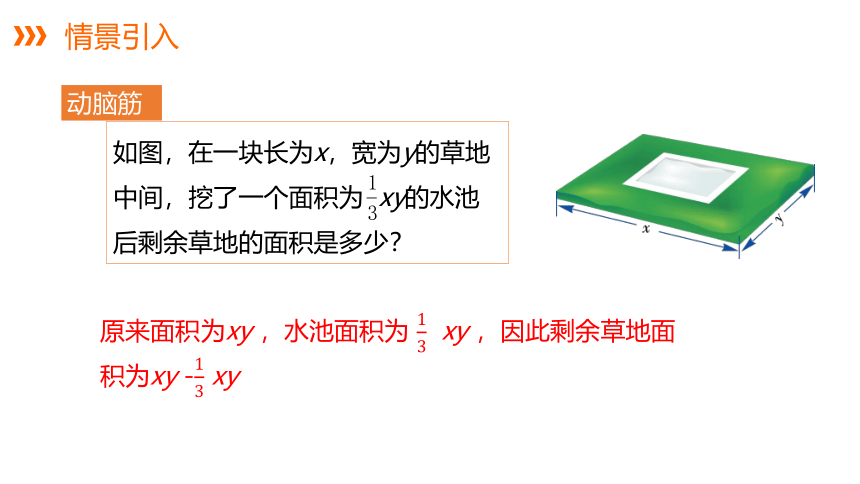
如图,在一块长为x,宽为y的草地中间,挖了一个面积为 xy的水池后剩余草地的面积是多少?
原来面积为xy ,水池面积为 xy ,因此剩余草地面积为xy - xy
情景引入
像多项式xy - xy中的项xy, - xy,它们含有的字母相同,并且相同的字母的指数也分别相同,称他们为同类项。
例如在多项式x2y +3x +1–4x-5x2y–5中,同类项有x2y与-5x2y,3x与–4x,1与-5.
获取新知
1.判断下列各组的两项是不是同类项?是的打“√”,不是的打“×”,并说明理由.
(1)3a2b与 ab2;( )
(2)2πr2与6r2;( )
(3)5与-8;( )
2.请写出一个与-a2b3是同类项的式子_________________.
×,相同字母指数不同
√
√
8a2b3
随堂演练
同类项:所含字母相同,并且相同字母的指数也分别相等的项叫做同类项.
(1)两个相同:字母相同;相同字母的次数相同;
(2)两个无关:与系数大小无关;与字母顺序无关;
(3)所有的常数项都是同类项.
说明:
获取新知
议一议
多项式x2y +3x +1–4x-5x2y–5中的同类项可以合并吗?
我想可以,因为多项式中的字母表示的是数,所以我们可以运用交换律、结合律、分配律把多项式中的同类项进行合并。
获取新知
x2y+3x+1-4x-5x2y-5
解
(交换律)
(结合律)
=x2y-5x2y+3x-4x+1-5
(分配律)
把多项式中的同类项合并成一项,叫做合并同类项
获取新知
(1)如果2a2bn+1与-4amb3是同类项,则m= ,n= .
(2)在6xy-3x2-4x2y-5yx2+x2中没有同类项的项是 .
2
2
6xy
分析:(1)根据同类项的定义,可知a的指数相同,b的指数也相同,即m=2,n+1=3.
随堂演练
解:
合并同类项:
例1
合并同类项时,只要把它们的系数相加,字母和字母的指数不变。
例题讲解
例2. 合并下式中的同类项:
(1)
(2)
解:
(1)
(1)
1.将同类项在底下划线标出;
2.运用加法的交换律和结合律,把同类项放在一起;
3.合并同类项.
注意:对于不同的同类项,分别用不同的线标出.
例题讲解
“合并同类项”的方法:
一找,找出多项式中的同类项,不同类的同类项用不同的标记标出;
二移,利用加法的交换律,将不同类的同类项集中到不同的括号内;
三合,将同一括号内的同类项相加即可.
系数相加,字母及其指数不变
获取新知
合并同类项:
(1)8x+2x2-2x+x2+1;
(2)5ab+8-2a2-2ab-3.
解:(1)原式=(8x-2x)+(2x2+x2)+1
=6x+3x2+1
(2)原式=(5ab-2ab)-2a2+(8-3)
=3ab-2a2+5
随堂演练
多项式x3-4x2+7x2-2x-5与多项式x3+3x2-6x+4x-5 相等吗?
说一说
两个式子合并同类项后都等于x3+3x2-2x-5 .
两个多项式分别经过合并同类项后,如果它们的对应项系数都相等,那么称这两个多项式相等
获取新知
(1)求多项式 的值,其中x = ;
(2)求多项式 的值, 其中a= ,b=2,c=-3.
分析:在多项式求值时,可以先将多项式中的同类项合并,然后再代入求值,这样可以简化计算.
解:(1)
当x = 时,原式=
(2)
当a= ,b=2,c=-3时,原式=1.
随堂演练
同 类 项
合并同类项
两个标准
法则
(1)所含字母相同;
(2)相同字母的指数分别相同;
(1)系数相加作为结果的系数。
(2)字母与字母的指数不变。
课堂小结
第2章 代数式
2.5 第1课时 合并同类项
单项式:由数与字母的积组成的代数式。(单独的数和字母也是单项式);
系数:单项式中,与字母相乘的数;
次数:一个单项式中,所有字母的指数的和;
多项式:由几个单项式的和组成的代数式;
项:组成多项式的没和单项式;
常数项:不含字母的项
旧知回顾
1.单项式-3a2bc的系数是______,次数是____.
2.多项式3x2y-xy3+y2- 的次数是_____,常数项是_____,.
-3
4
4
旧知回顾
动脑筋
如图,在一块长为x,宽为y的草地中间,挖了一个面积为 xy的水池后剩余草地的面积是多少?
原来面积为xy ,水池面积为 xy ,因此剩余草地面积为xy - xy
情景引入
像多项式xy - xy中的项xy, - xy,它们含有的字母相同,并且相同的字母的指数也分别相同,称他们为同类项。
例如在多项式x2y +3x +1–4x-5x2y–5中,同类项有x2y与-5x2y,3x与–4x,1与-5.
获取新知
1.判断下列各组的两项是不是同类项?是的打“√”,不是的打“×”,并说明理由.
(1)3a2b与 ab2;( )
(2)2πr2与6r2;( )
(3)5与-8;( )
2.请写出一个与-a2b3是同类项的式子_________________.
×,相同字母指数不同
√
√
8a2b3
随堂演练
同类项:所含字母相同,并且相同字母的指数也分别相等的项叫做同类项.
(1)两个相同:字母相同;相同字母的次数相同;
(2)两个无关:与系数大小无关;与字母顺序无关;
(3)所有的常数项都是同类项.
说明:
获取新知
议一议
多项式x2y +3x +1–4x-5x2y–5中的同类项可以合并吗?
我想可以,因为多项式中的字母表示的是数,所以我们可以运用交换律、结合律、分配律把多项式中的同类项进行合并。
获取新知
x2y+3x+1-4x-5x2y-5
解
(交换律)
(结合律)
=x2y-5x2y+3x-4x+1-5
(分配律)
把多项式中的同类项合并成一项,叫做合并同类项
获取新知
(1)如果2a2bn+1与-4amb3是同类项,则m= ,n= .
(2)在6xy-3x2-4x2y-5yx2+x2中没有同类项的项是 .
2
2
6xy
分析:(1)根据同类项的定义,可知a的指数相同,b的指数也相同,即m=2,n+1=3.
随堂演练
解:
合并同类项:
例1
合并同类项时,只要把它们的系数相加,字母和字母的指数不变。
例题讲解
例2. 合并下式中的同类项:
(1)
(2)
解:
(1)
(1)
1.将同类项在底下划线标出;
2.运用加法的交换律和结合律,把同类项放在一起;
3.合并同类项.
注意:对于不同的同类项,分别用不同的线标出.
例题讲解
“合并同类项”的方法:
一找,找出多项式中的同类项,不同类的同类项用不同的标记标出;
二移,利用加法的交换律,将不同类的同类项集中到不同的括号内;
三合,将同一括号内的同类项相加即可.
系数相加,字母及其指数不变
获取新知
合并同类项:
(1)8x+2x2-2x+x2+1;
(2)5ab+8-2a2-2ab-3.
解:(1)原式=(8x-2x)+(2x2+x2)+1
=6x+3x2+1
(2)原式=(5ab-2ab)-2a2+(8-3)
=3ab-2a2+5
随堂演练
多项式x3-4x2+7x2-2x-5与多项式x3+3x2-6x+4x-5 相等吗?
说一说
两个式子合并同类项后都等于x3+3x2-2x-5 .
两个多项式分别经过合并同类项后,如果它们的对应项系数都相等,那么称这两个多项式相等
获取新知
(1)求多项式 的值,其中x = ;
(2)求多项式 的值, 其中a= ,b=2,c=-3.
分析:在多项式求值时,可以先将多项式中的同类项合并,然后再代入求值,这样可以简化计算.
解:(1)
当x = 时,原式=
(2)
当a= ,b=2,c=-3时,原式=1.
随堂演练
同 类 项
合并同类项
两个标准
法则
(1)所含字母相同;
(2)相同字母的指数分别相同;
(1)系数相加作为结果的系数。
(2)字母与字母的指数不变。
课堂小结
同课章节目录
