湘教版数学七年级上册同步课件:3.3 第2课时 利用去括号解一元一次方程(17张ppt)
文档属性
| 名称 | 湘教版数学七年级上册同步课件:3.3 第2课时 利用去括号解一元一次方程(17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 182.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 08:18:13 | ||
图片预览






文档简介
(共17张PPT)
第3章 一元一次方程
3.3 第2课时 利用去括号解一元一次方程
1、解下列方程:
(1) 5x-7=2x-10;
(2) -0.3x+3=9+1.2x.
解:(1)移项,得
5x-2x=-10+7,
合并同类项,得
-3x=-3,
系数化为1,得
x=1.
(2)移项,得
-0.3x-1.2x=9-3,
合并同类项,得
-1.5x=6,
系数化为1,得
x=-4.
旧知回顾
2、如果x=-7是方程4x+6=ax-1的解,试求代数式 的值.
解:把x=-7代入方程,得
4×(-7)+6=a×(-7)-1,
解得a=3.
把a=3代入,
旧知回顾
动脑筋
一艘轮船在A,B两个码头之间航行,顺水航行需4h,逆水航行需5h. 已知水流速度为2km/h,求轮船在静水中的航行速度.
情景引入
轮船顺水的航行速度
= 轮船在静水中的速度+水流速度.
轮船逆水的航行速度= 轮船在静水中的速度-水流速度.
情景引入
因此,设轮船在静水中的航行速度为x km/h,则根据等量关系可得
4(x+2)= 5(x-2) .
去括号,得 4x + 8 = 5x - 10 .
移项,得 4x-5x= -8-10 .
合并同类项,得 -x =-18 .
两边都除以-1,得 x = 18 .
因此,轮船在静水中的航行速度为18 km/h.
本问题涉及的等量关系有:
顺水航行的路程 = 逆水航行的路程.
获取新知
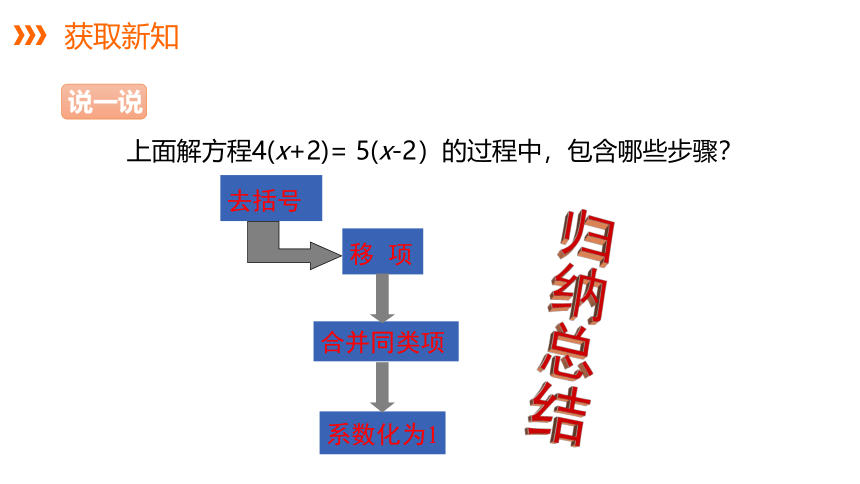
说一说
上面解方程4(x+2)= 5(x-2)的过程中,包含哪些步骤?
移 项
合并同类项
系数化为1
去括号
归纳总结
获取新知
去括号法则:
1.括号前是“+”号,运用加法结合律把括号去掉,原括号里各项的符号都______.
2.括号前是“-”号,把括号和它前面的“-”号去掉,原括号里各项的符号都要______.
不变
改变
在第二章代数式里卖弄我们学了去括号法则:
获取新知
1、将-[-(m-n)]去括号得( )
A.m-n B.-m-n
C.-m+n D.m+n
A
2、下列去括号不正确的是( )
A.a2-(a-b+c)=a2-a+b-c
B.x2-(-x+y)-(m-n)=x2-x+y-m+n
C.x2-3(x+2)=x2-3x-6
D.-(a-2b)-(c-d)=-a+2b-c+d
B
随堂演练
解方程: 3(2x -1) = 3x + 1.
解
去括号,得 6x-3 = 3x+1
合并同类项,得 3x = 4
移项,得 6x -3x = 1+3
两边都除以3,得 x =
因此,原方程的解是 x = .
例2
例题讲解
解方程:-2(x-1)=4.
解:去括号,得-2x+2=4.
移项,得-2x=4-2.
化简,得-2x=2.
方程两边同除以-2,得x=-1.
你能想出不同的解法吗?
随堂演练
解法二:
-2 (x-1) =4.
方程两边同除以-2,得x-1=-2.
移项,得x=-2+1.
即x=-1.
看做整体可解出它,进而解出x
讨论:比较上面两种解法,说说它们的区别.
随堂演练
1.下面方程的求解是否正确?如不正确,请改正.
解方程 2(2x+3)=2+x
解 去括号,得 4x+3=2+x
移项,得 4x +x = 2-3
化简,得 5x = -1
方程两边都除以5 ,得
x = -
应改为4 x +6 =2+x
应改为4 x– x = 2-6
应改为3x =-4
应改为 x =
方程两边都除以3,得
随堂演练
2. 解下列方程.
(1) (4y+8)+2(3y-7)= 0 ;
(2) 2(2x -1)-2(4x+3)= 7;
(3) 3(x -4)= 4x-1.
随堂演练
解
(1) 原方程为(4y+8)+2(3y-7)= 0
去括号,得 4y+8+6y-14= 0
移项,得 4y+6y = 14-8
化简,得 10y = 6
方程两边同除以 10, y =
(2) 原方程为2(2x -1)-2(4x+3)= 7
去括号,得 4x-2-8x-6= 7
移项,得 4x-8x = 2+6+7
化简,得 -4x = 15
方程两边同除以 -4, x = -
随堂演练
(3) 原方程为 3(x -4)= 4x-1
去括号,得 3x -12 = 4x-1
移项,得 3x -4x = 12-1
化简,得 - x = 11
方程两边同除以 -11,
x = -11
随堂演练
利用去括号解一元一次方程
去括号解一元一次方程的应用
解含有括号的一元一次方程
移项
④系数化1
合并同类项
去括号
课堂小结
第3章 一元一次方程
3.3 第2课时 利用去括号解一元一次方程
1、解下列方程:
(1) 5x-7=2x-10;
(2) -0.3x+3=9+1.2x.
解:(1)移项,得
5x-2x=-10+7,
合并同类项,得
-3x=-3,
系数化为1,得
x=1.
(2)移项,得
-0.3x-1.2x=9-3,
合并同类项,得
-1.5x=6,
系数化为1,得
x=-4.
旧知回顾
2、如果x=-7是方程4x+6=ax-1的解,试求代数式 的值.
解:把x=-7代入方程,得
4×(-7)+6=a×(-7)-1,
解得a=3.
把a=3代入,
旧知回顾
动脑筋
一艘轮船在A,B两个码头之间航行,顺水航行需4h,逆水航行需5h. 已知水流速度为2km/h,求轮船在静水中的航行速度.
情景引入
轮船顺水的航行速度
= 轮船在静水中的速度+水流速度.
轮船逆水的航行速度= 轮船在静水中的速度-水流速度.
情景引入
因此,设轮船在静水中的航行速度为x km/h,则根据等量关系可得
4(x+2)= 5(x-2) .
去括号,得 4x + 8 = 5x - 10 .
移项,得 4x-5x= -8-10 .
合并同类项,得 -x =-18 .
两边都除以-1,得 x = 18 .
因此,轮船在静水中的航行速度为18 km/h.
本问题涉及的等量关系有:
顺水航行的路程 = 逆水航行的路程.
获取新知
说一说
上面解方程4(x+2)= 5(x-2)的过程中,包含哪些步骤?
移 项
合并同类项
系数化为1
去括号
归纳总结
获取新知
去括号法则:
1.括号前是“+”号,运用加法结合律把括号去掉,原括号里各项的符号都______.
2.括号前是“-”号,把括号和它前面的“-”号去掉,原括号里各项的符号都要______.
不变
改变
在第二章代数式里卖弄我们学了去括号法则:
获取新知
1、将-[-(m-n)]去括号得( )
A.m-n B.-m-n
C.-m+n D.m+n
A
2、下列去括号不正确的是( )
A.a2-(a-b+c)=a2-a+b-c
B.x2-(-x+y)-(m-n)=x2-x+y-m+n
C.x2-3(x+2)=x2-3x-6
D.-(a-2b)-(c-d)=-a+2b-c+d
B
随堂演练
解方程: 3(2x -1) = 3x + 1.
解
去括号,得 6x-3 = 3x+1
合并同类项,得 3x = 4
移项,得 6x -3x = 1+3
两边都除以3,得 x =
因此,原方程的解是 x = .
例2
例题讲解
解方程:-2(x-1)=4.
解:去括号,得-2x+2=4.
移项,得-2x=4-2.
化简,得-2x=2.
方程两边同除以-2,得x=-1.
你能想出不同的解法吗?
随堂演练
解法二:
-2 (x-1) =4.
方程两边同除以-2,得x-1=-2.
移项,得x=-2+1.
即x=-1.
看做整体可解出它,进而解出x
讨论:比较上面两种解法,说说它们的区别.
随堂演练
1.下面方程的求解是否正确?如不正确,请改正.
解方程 2(2x+3)=2+x
解 去括号,得 4x+3=2+x
移项,得 4x +x = 2-3
化简,得 5x = -1
方程两边都除以5 ,得
x = -
应改为4 x +6 =2+x
应改为4 x– x = 2-6
应改为3x =-4
应改为 x =
方程两边都除以3,得
随堂演练
2. 解下列方程.
(1) (4y+8)+2(3y-7)= 0 ;
(2) 2(2x -1)-2(4x+3)= 7;
(3) 3(x -4)= 4x-1.
随堂演练
解
(1) 原方程为(4y+8)+2(3y-7)= 0
去括号,得 4y+8+6y-14= 0
移项,得 4y+6y = 14-8
化简,得 10y = 6
方程两边同除以 10, y =
(2) 原方程为2(2x -1)-2(4x+3)= 7
去括号,得 4x-2-8x-6= 7
移项,得 4x-8x = 2+6+7
化简,得 -4x = 15
方程两边同除以 -4, x = -
随堂演练
(3) 原方程为 3(x -4)= 4x-1
去括号,得 3x -12 = 4x-1
移项,得 3x -4x = 12-1
化简,得 - x = 11
方程两边同除以 -11,
x = -11
随堂演练
利用去括号解一元一次方程
去括号解一元一次方程的应用
解含有括号的一元一次方程
移项
④系数化1
合并同类项
去括号
课堂小结
同课章节目录
