湘教版数学七年级上册同步课件:3.3 第3课时 利用去分母解一元一次方程(16张ppt)
文档属性
| 名称 | 湘教版数学七年级上册同步课件:3.3 第3课时 利用去分母解一元一次方程(16张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 467.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 08:20:58 | ||
图片预览

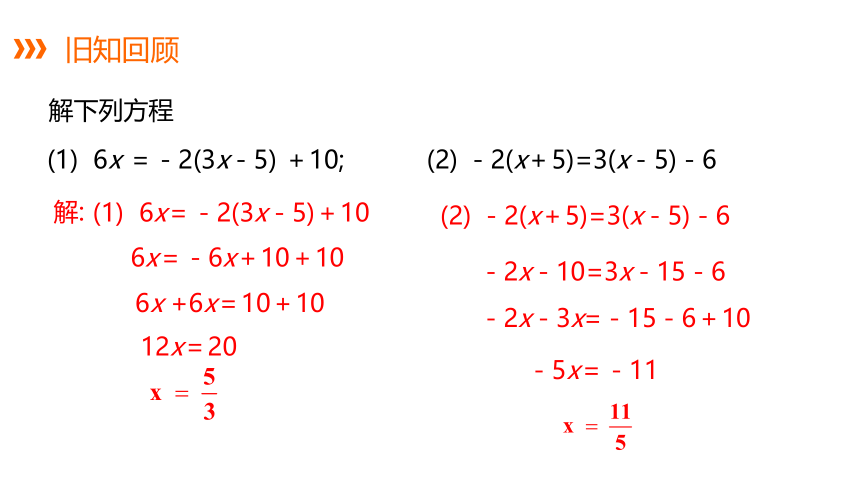





文档简介
(共16张PPT)
第3章 一元一次方程
3.3 第3课时 利用去分母
(1) 6x =-2(3x-5) +10; (2) -2(x+5)=3(x-5)-6
解下列方程
解:
(1) 6x=-2(3x-5)+10
6x=-6x+10+10
6x +6x=10+10
12x=20
(2) -2(x+5)=3(x-5)-6
-2x-10=3x-15-6
-2x-3x=-15-6+10
-5x=-11
旧知回顾
1.解方程:2(x-2)-3(4x-1)=9(1-x).
解:2x-4-12x+3=9-9x,
-x=10,
x=-10.
2.求下列各数的最小公倍数:
(1)2,3,4;
(2)3,6,8;
(3)3,4,18.
12
24
36
旧知回顾
动脑筋
刺绣一件作品,甲单独绣需要15天完成,乙单独绣需要12天完成. 现在甲先单独绣1天,接着乙又单独绣4天,剩下的工作由甲、乙两人合绣. 问再合绣多少天可以完成这件作品?
情景引入
本问题涉及的等量关系有:
甲完成的工作量 + 乙完成的工作量 = 总工作量.
如果剩下的工作两人合绣x天就可完成,
因此,设工作总量为1,则甲每天完成工作总量的 ,乙每天完成工作总量的 .
那么甲共绣了(x+1)天,完成的工作量为 ;
乙共绣了(x+4)天,完成的工作量为 .
获取新知
即 4(x+1)+5(x+4)=60.
去括号,得 4x+4+5x+20=60.
移项,合并同类项得 9x=36.
方程两边都除以9,得 x=4.
因此,两人再合绣4天,就可完成这件作品.
根据等量关系,得
方程两边都乘60,得
获取新知
火车用26秒的时间通过一个长256米的隧道(即从车头进入入口到车尾离开出口),这列火车又以16秒的时间通过了长96米的隧道,求火车的长度.
解:设火车的长度为x米,列方程:
解得 x =160.
答:火车的长度为160米.
获取新知
解方程:
例3
解
去分母,得 5(3x -1)-2(2-x)=10x
去括号,得 15x -5-4+2x= 10x
移项,合并同类项,得 7x = 9
方程两边都除以7,得
x =
因此,原方程的解是 .
例题讲解
解一元一次方程有哪些基本步骤?
一元一次方程
ax=b(a,b是常数,a≠0)
去分母,去括号,
移项,合并同类项得
两边都除以a得
_______→去括号→ _______→合并同类项→ _____________________.
去分母
移项
把未知数的系数化为1
获取新知
1. 下面各题中的去分母对吗?如不对,请改正.
(1) - = 2,去分母,得5x-2x+3 = 2;
(2) + = 4,去分母,得4(3x+1)+25x= 80.
不对,应为 25x-3(2x-3)=30
对
随堂演练
2. 解下列方程:
(1) ;
(2) ;
(3) ;
(4)50%(3x -1)-20%(2-x)=x .
随堂演练
解:
去分母,得 × 4 = × 4
(y -1)×2 = 1-2y
去括号,得 2y-2 = 1-2y
移项,得 2y +2y = 2+1
化简,得 4y = 3
方程两边同除以 4, y =
(1)
随堂演练
解:
去分母,得 × 6 = × 6
(5+3x)×3 = (3+5x)×2
去括号,得 15+9x = 6+10x
移项,得 9x -10x = 6-15
化简,得 -1x = -9
方程两边同除以 1, x = 9
(2) =
随堂演练
解:
去分母,得 × 24 - × 24 =1
(2x-1)×4 - (5x+1)×3=1×24
去括号,得 8x -4 -15x – 3 =24
移项,得 8x -15x = 4+3+24
化简,得 -7x = 31
方程两边同除以 -7, x = -
(3) - = 1.
随堂演练
解:
整理,得 0.5(3x-1)- 0.2(2-x) = x
去括号,得 1.5x-0.5-0.4+0.2x= x
移项,得 1.5x+0.2x -x = 0.5+0.4
化简,得 0.7x = 0.9
方程两边同除以 0.7, x =
(4)50%(3x -1)-20%(2-x)=x .
随堂演练
变形名称 具体的做法
去分母 乘所有的分母的最小公倍数.依据是等式性质二.
去括号 先去小括号,再去中括号,最后去大括号.依据是去括号法则和乘法分配律.
移项 把含有未知数的项移到一边,常数项移到另一边.“过桥变号”,依据是等式性质一.
合并同类项 将未知数的系数相加,常数项相加.依据是乘法分配律.
系数化为1 在方程的两边除以未知数的系数.依据是等式性质二.
解一元一次方程的一般步骤
课堂小结
第3章 一元一次方程
3.3 第3课时 利用去分母
(1) 6x =-2(3x-5) +10; (2) -2(x+5)=3(x-5)-6
解下列方程
解:
(1) 6x=-2(3x-5)+10
6x=-6x+10+10
6x +6x=10+10
12x=20
(2) -2(x+5)=3(x-5)-6
-2x-10=3x-15-6
-2x-3x=-15-6+10
-5x=-11
旧知回顾
1.解方程:2(x-2)-3(4x-1)=9(1-x).
解:2x-4-12x+3=9-9x,
-x=10,
x=-10.
2.求下列各数的最小公倍数:
(1)2,3,4;
(2)3,6,8;
(3)3,4,18.
12
24
36
旧知回顾
动脑筋
刺绣一件作品,甲单独绣需要15天完成,乙单独绣需要12天完成. 现在甲先单独绣1天,接着乙又单独绣4天,剩下的工作由甲、乙两人合绣. 问再合绣多少天可以完成这件作品?
情景引入
本问题涉及的等量关系有:
甲完成的工作量 + 乙完成的工作量 = 总工作量.
如果剩下的工作两人合绣x天就可完成,
因此,设工作总量为1,则甲每天完成工作总量的 ,乙每天完成工作总量的 .
那么甲共绣了(x+1)天,完成的工作量为 ;
乙共绣了(x+4)天,完成的工作量为 .
获取新知
即 4(x+1)+5(x+4)=60.
去括号,得 4x+4+5x+20=60.
移项,合并同类项得 9x=36.
方程两边都除以9,得 x=4.
因此,两人再合绣4天,就可完成这件作品.
根据等量关系,得
方程两边都乘60,得
获取新知
火车用26秒的时间通过一个长256米的隧道(即从车头进入入口到车尾离开出口),这列火车又以16秒的时间通过了长96米的隧道,求火车的长度.
解:设火车的长度为x米,列方程:
解得 x =160.
答:火车的长度为160米.
获取新知
解方程:
例3
解
去分母,得 5(3x -1)-2(2-x)=10x
去括号,得 15x -5-4+2x= 10x
移项,合并同类项,得 7x = 9
方程两边都除以7,得
x =
因此,原方程的解是 .
例题讲解
解一元一次方程有哪些基本步骤?
一元一次方程
ax=b(a,b是常数,a≠0)
去分母,去括号,
移项,合并同类项得
两边都除以a得
_______→去括号→ _______→合并同类项→ _____________________.
去分母
移项
把未知数的系数化为1
获取新知
1. 下面各题中的去分母对吗?如不对,请改正.
(1) - = 2,去分母,得5x-2x+3 = 2;
(2) + = 4,去分母,得4(3x+1)+25x= 80.
不对,应为 25x-3(2x-3)=30
对
随堂演练
2. 解下列方程:
(1) ;
(2) ;
(3) ;
(4)50%(3x -1)-20%(2-x)=x .
随堂演练
解:
去分母,得 × 4 = × 4
(y -1)×2 = 1-2y
去括号,得 2y-2 = 1-2y
移项,得 2y +2y = 2+1
化简,得 4y = 3
方程两边同除以 4, y =
(1)
随堂演练
解:
去分母,得 × 6 = × 6
(5+3x)×3 = (3+5x)×2
去括号,得 15+9x = 6+10x
移项,得 9x -10x = 6-15
化简,得 -1x = -9
方程两边同除以 1, x = 9
(2) =
随堂演练
解:
去分母,得 × 24 - × 24 =1
(2x-1)×4 - (5x+1)×3=1×24
去括号,得 8x -4 -15x – 3 =24
移项,得 8x -15x = 4+3+24
化简,得 -7x = 31
方程两边同除以 -7, x = -
(3) - = 1.
随堂演练
解:
整理,得 0.5(3x-1)- 0.2(2-x) = x
去括号,得 1.5x-0.5-0.4+0.2x= x
移项,得 1.5x+0.2x -x = 0.5+0.4
化简,得 0.7x = 0.9
方程两边同除以 0.7, x =
(4)50%(3x -1)-20%(2-x)=x .
随堂演练
变形名称 具体的做法
去分母 乘所有的分母的最小公倍数.依据是等式性质二.
去括号 先去小括号,再去中括号,最后去大括号.依据是去括号法则和乘法分配律.
移项 把含有未知数的项移到一边,常数项移到另一边.“过桥变号”,依据是等式性质一.
合并同类项 将未知数的系数相加,常数项相加.依据是乘法分配律.
系数化为1 在方程的两边除以未知数的系数.依据是等式性质二.
解一元一次方程的一般步骤
课堂小结
同课章节目录
