湘教版数学七年级上册同步课件:4.3.2 第1课时 角的度量与计算(共16张PPT)
文档属性
| 名称 | 湘教版数学七年级上册同步课件:4.3.2 第1课时 角的度量与计算(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 225.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
第4章 图形的认识
4.3.2 第1课时 角的度量与计算
1、下列语句正确的是 ( )
A. 两条直线相交,组成的图形叫做角
B. 两条有公共端点的线段组成的图形叫做角
C. 两条有公共点的射线组成的图形叫做角
D. 从同一点引出的两条射线组成的图形叫做角
D
2、下列说法不正确的是 ( )
A. ∠AOB 的顶点是O
B. 射线BO,AO分别是∠AOB的两条边
C. ∠AOB的边是两条射线
D. ∠AOB与∠BOA表示同一个角
B
旧知回顾
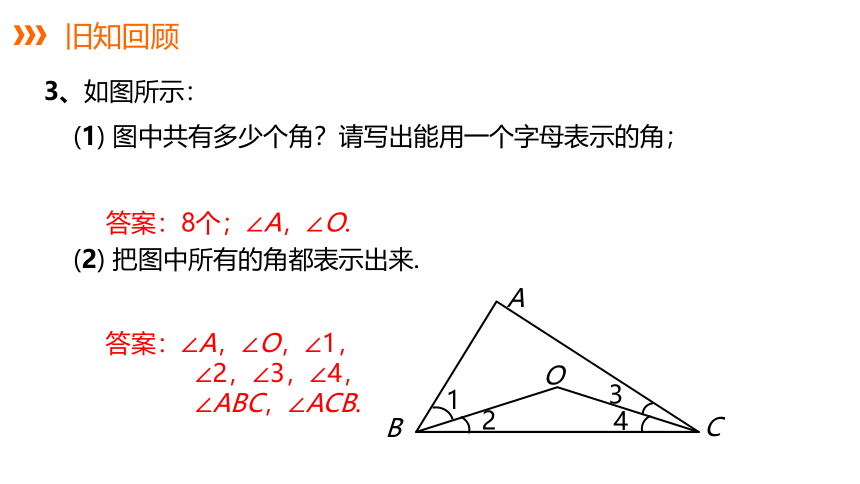
3、如图所示:
(1) 图中共有多少个角?请写出能用一个字母表示的角;
(2) 把图中所有的角都表示出来.
A
B
C
4
3
2
1
O
答案:8个;∠A,∠O.
答案:∠A,∠O,∠1,
∠2,∠3,∠4,
∠ABC,∠ACB.
旧知回顾
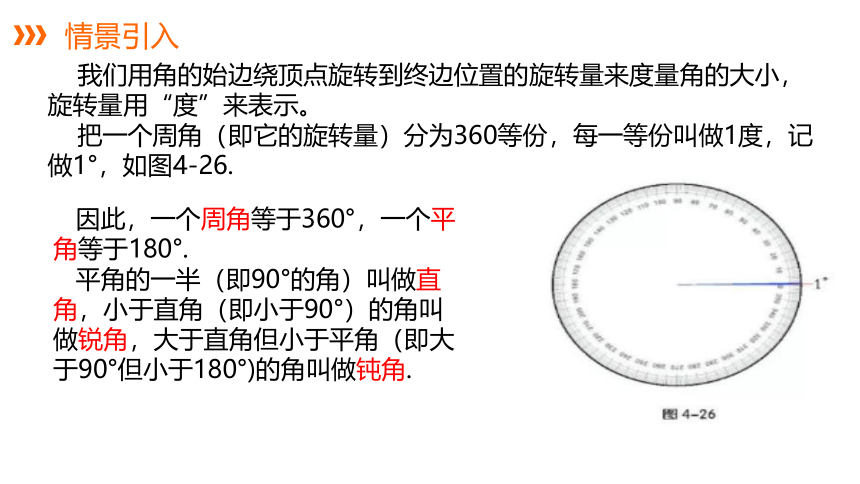
我们用角的始边绕顶点旋转到终边位置的旋转量来度量角的大小,旋转量用“度”来表示。
把一个周角(即它的旋转量)分为360等份,每一等份叫做1度,记做1°,如图4-26.
因此,一个周角等于360°,一个平角等于180°.
平角的一半(即90°的角)叫做直角,小于直角(即小于90°)的角叫做锐角,大于直角但小于平角(即大于90°但小于180°)的角叫做钝角.
情景引入
1、两个锐角的和( )
A.一定是锐角
B.一定是直角
C.一定是钝角
D.可能是锐角、直角或钝角
D
2、 周角=_____,60°=____平角= _____直角.
60°
获取新知
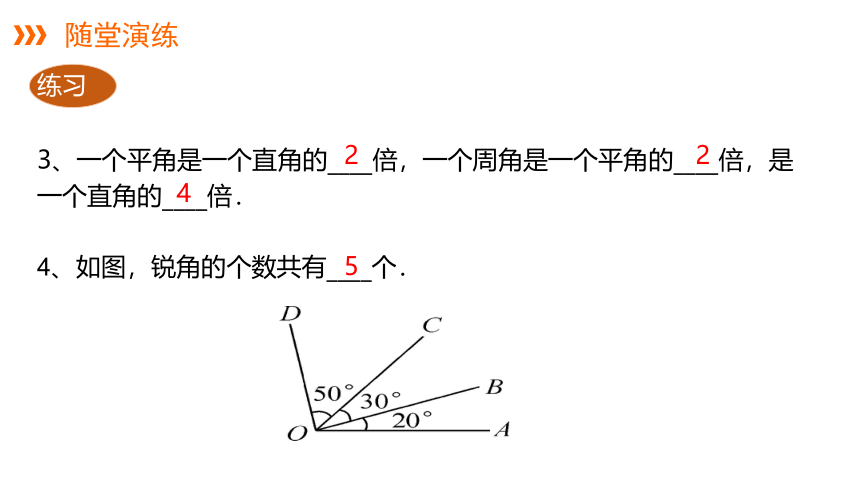
3、一个平角是一个直角的____倍,一个周角是一个平角的____倍,是一个直角的____倍.
练习
4、如图,锐角的个数共有____个.
2
2
4
5
随堂演练
获取新知
我们可以用量角器来测量一个角的大小,但有时一个角的度数并不一定是整数,这时与长度单位一样,需要考虑用更小的单位来度量,把1°的角分成60等份,每一等份叫做1分,记做1';再把l'的角分成60等份,每一等份叫做1秒,记做1”、即
度、分、秒是角的基本度量单位.度、分、秒之间的换算是60进制,这与时间的时、分、秒之间的换算是一样的。
用度、分、秒表示54.26°.
解:54.26°= 54°+ 0.26°.
又 0.26°= 0.26× 60′
= 15.6′= 15′+0.6′,
而 0.6′= 0.6 × 60″= 36″,
因此,54.26°= 54°15′36″.
按1°=60′,1′=60″先把度化成分,再把分化成秒
(小数化整数)
例1
例题讲解
例2 把45°25′48″化成度.
解:45°25′48″
=45°+25′+48×(1/60)'
=45°+25.8'
=45°+25.8×(1/60)°
=45.43°
按1″=(1/60)′,1′=(1/60)°先把秒化成分,再把分化成度(整数化小数)
例题讲解
度
分
秒
×60
×60
×3600
÷60
÷3600
÷60
度分秒进率关系图
例3.计算:
(1)37°28′+ 24°35′; (2)83°20′-45°38′20″;
(3)25°53′28″×5; (4)15°20′÷6.
解:(1) 37°28′+ 24°35′
= 61°63′
= 62°3′;
(2) 83°20′- 45°38′20″
= 82°79′60″- 45°38′20″
= 37°41′40″.
逢“60”进“1”
不够减,向前一位借“1”
例题讲解
(3)25°53′28″×5
=25°×5+53′×5+28″×5
=125°+265′+140″
=129°27′20″.
(4)15°20′÷6
=12°200′÷6
=12°÷6+200′÷6
=2°+198′÷6+2′÷6
=2°+33′+120″÷6
=2°33′20″.
例题讲解
在进行度、分、秒的加、减、乘、除运算时,要注意三点:
①度、分、秒均是60进制的;
②加、减法的运算,可以本着“度与度加减、分与分加减、秒与秒加减,不够减的时候借位”的原则;
③乘、除法运算可以按分配律来进行,不够除可以把余数化为低位的再除.
方法总结
2、比较大小:74.45°________74°45′
<
1、 填空:
(1)0.65°= ′;
(2)32.43°= ° ′ ″;
(3)120°38′54〃= °;
(4)108°40′24″ =________ °.
39
32
25
48
120.65
108.67
3、时钟4点15分时,时针和分针所成的角为_____.
37.5°
获取新知
4、(1)72°12′+50°40′30″;
(2)113°50′40″-57°48′42″.
(4)原式=113°49′100″-57°48′42″
=56°1′58″.
获取新知
角的度量与计算
角的分类
角的单位的换算
角的和、差计算
周角
钝角
锐角
平角
直角
课堂小结
第4章 图形的认识
4.3.2 第1课时 角的度量与计算
1、下列语句正确的是 ( )
A. 两条直线相交,组成的图形叫做角
B. 两条有公共端点的线段组成的图形叫做角
C. 两条有公共点的射线组成的图形叫做角
D. 从同一点引出的两条射线组成的图形叫做角
D
2、下列说法不正确的是 ( )
A. ∠AOB 的顶点是O
B. 射线BO,AO分别是∠AOB的两条边
C. ∠AOB的边是两条射线
D. ∠AOB与∠BOA表示同一个角
B
旧知回顾
3、如图所示:
(1) 图中共有多少个角?请写出能用一个字母表示的角;
(2) 把图中所有的角都表示出来.
A
B
C
4
3
2
1
O
答案:8个;∠A,∠O.
答案:∠A,∠O,∠1,
∠2,∠3,∠4,
∠ABC,∠ACB.
旧知回顾
我们用角的始边绕顶点旋转到终边位置的旋转量来度量角的大小,旋转量用“度”来表示。
把一个周角(即它的旋转量)分为360等份,每一等份叫做1度,记做1°,如图4-26.
因此,一个周角等于360°,一个平角等于180°.
平角的一半(即90°的角)叫做直角,小于直角(即小于90°)的角叫做锐角,大于直角但小于平角(即大于90°但小于180°)的角叫做钝角.
情景引入
1、两个锐角的和( )
A.一定是锐角
B.一定是直角
C.一定是钝角
D.可能是锐角、直角或钝角
D
2、 周角=_____,60°=____平角= _____直角.
60°
获取新知
3、一个平角是一个直角的____倍,一个周角是一个平角的____倍,是一个直角的____倍.
练习
4、如图,锐角的个数共有____个.
2
2
4
5
随堂演练
获取新知
我们可以用量角器来测量一个角的大小,但有时一个角的度数并不一定是整数,这时与长度单位一样,需要考虑用更小的单位来度量,把1°的角分成60等份,每一等份叫做1分,记做1';再把l'的角分成60等份,每一等份叫做1秒,记做1”、即
度、分、秒是角的基本度量单位.度、分、秒之间的换算是60进制,这与时间的时、分、秒之间的换算是一样的。
用度、分、秒表示54.26°.
解:54.26°= 54°+ 0.26°.
又 0.26°= 0.26× 60′
= 15.6′= 15′+0.6′,
而 0.6′= 0.6 × 60″= 36″,
因此,54.26°= 54°15′36″.
按1°=60′,1′=60″先把度化成分,再把分化成秒
(小数化整数)
例1
例题讲解
例2 把45°25′48″化成度.
解:45°25′48″
=45°+25′+48×(1/60)'
=45°+25.8'
=45°+25.8×(1/60)°
=45.43°
按1″=(1/60)′,1′=(1/60)°先把秒化成分,再把分化成度(整数化小数)
例题讲解
度
分
秒
×60
×60
×3600
÷60
÷3600
÷60
度分秒进率关系图
例3.计算:
(1)37°28′+ 24°35′; (2)83°20′-45°38′20″;
(3)25°53′28″×5; (4)15°20′÷6.
解:(1) 37°28′+ 24°35′
= 61°63′
= 62°3′;
(2) 83°20′- 45°38′20″
= 82°79′60″- 45°38′20″
= 37°41′40″.
逢“60”进“1”
不够减,向前一位借“1”
例题讲解
(3)25°53′28″×5
=25°×5+53′×5+28″×5
=125°+265′+140″
=129°27′20″.
(4)15°20′÷6
=12°200′÷6
=12°÷6+200′÷6
=2°+198′÷6+2′÷6
=2°+33′+120″÷6
=2°33′20″.
例题讲解
在进行度、分、秒的加、减、乘、除运算时,要注意三点:
①度、分、秒均是60进制的;
②加、减法的运算,可以本着“度与度加减、分与分加减、秒与秒加减,不够减的时候借位”的原则;
③乘、除法运算可以按分配律来进行,不够除可以把余数化为低位的再除.
方法总结
2、比较大小:74.45°________74°45′
<
1、 填空:
(1)0.65°= ′;
(2)32.43°= ° ′ ″;
(3)120°38′54〃= °;
(4)108°40′24″ =________ °.
39
32
25
48
120.65
108.67
3、时钟4点15分时,时针和分针所成的角为_____.
37.5°
获取新知
4、(1)72°12′+50°40′30″;
(2)113°50′40″-57°48′42″.
(4)原式=113°49′100″-57°48′42″
=56°1′58″.
获取新知
角的度量与计算
角的分类
角的单位的换算
角的和、差计算
周角
钝角
锐角
平角
直角
课堂小结
同课章节目录
