湘教版数学七年级上册同步课件:4.3.1角与角的大小比较(共15张PPT)
文档属性
| 名称 | 湘教版数学七年级上册同步课件:4.3.1角与角的大小比较(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 510.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
第4章 分式
4.3.1 角与角的大小比较
观察
如图,钟面上的时针和分针、圆规的两只脚之间、折扇的扇骨与扇骨之间都给我们以什么样的形象?
情景引入
这里有许多角……
角是由具有公共端点的两条射线组成的图形。
获取新知
观察角的图像,你能归纳出角的概念吗?尝试去描述一下角是由什么组成的图形?
获取新知
O
A
B
有公共端点的两条射线组成的图形叫做角. (静态定义)
始边
终边
一条射线绕着它的端点从一个位置旋转到另一位置时所成的图形叫做角. (动态定义)
公共端点
—-角的顶点
两条射线
—-角的边
角的内部
获取新知
其中,射线的端点O叫做角的顶点。射线原来所在的位置OA叫做角的始边,旋转后的位置OB叫做角的终边,角的始边和终边统称为角的边。从始边旋转到终边所扫过的区域,叫做角的内部。
角的大小由角的始边绕顶点旋转至终边时旋转的量的大小决定。
获取新知
O
A
B
O
A
(B)
平角
周角
O
A
B
(B)
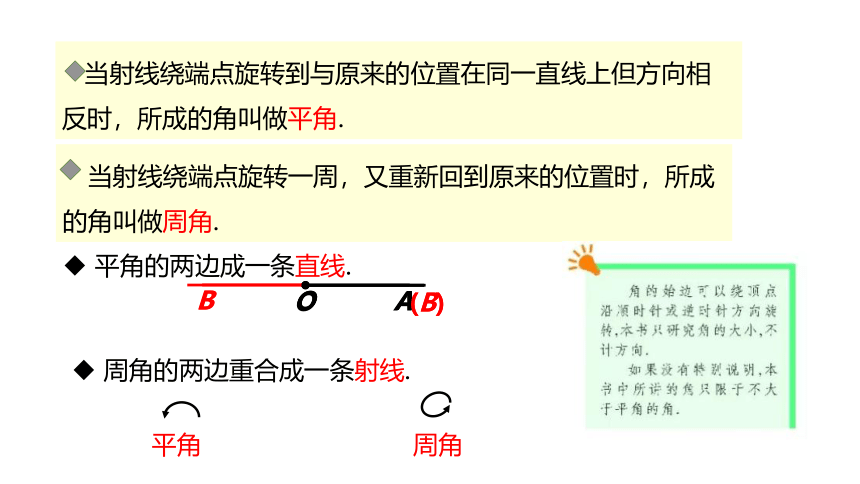
平角的两边成一条直线.
周角的两边重合成一条射线.
当射线绕端点旋转到与原来的位置在同一直线上但方向相反时,所成的角叫做平角.
当射线绕端点旋转一周,又重新回到原来的位置时,所成的角叫做周角.
角通常可用如图所示的方法来表示.
获取新知
方法 图示 记法 适用范围
1.用三个大写字母表示 ∠AOB 或∠BOA 任何角
2.用一个大写字母表示 ∠O 顶点处只有一个角
3.用一个数字或希腊字母来表示 有弧线和数字
弧线和小写希腊字母
O
A
B
O
1
角的表示方法总结
获取新知
探究
怎样比较图中的∠ABC和∠DEF的大小?
可用量角器量
与线段长短的比较类似,可以把它们叠合在一起比较大小。
先将∠DEF移动,使它的顶点E与∠ABC的顶点B重合,并且使∠DEF的一条边EF与∠ABC的一条边BC重合,边ED,BA都在BC的同侧,这时可能出现的情形如下表:
获取新知
情形 图形 ∠ABC与∠DEF的关系
ED与BA重合 ∠ABC = ∠DEF
ED落在∠ABC内部 ∠ABC > ∠DEF
ED落在∠ABC外部 ∠ABC < ∠DEF
获取新知
以一个角的顶点为端点的一条射线,如果把这个角分成两个相等的角,那么这条射线叫做这个角的平分线。如图,若OC是∠AOB的平分线,则∠AOC=∠BOC=1/2∠AOB.
获取新知
1、 判断
(1) 直线是一个平角 ( )
(2) 如图①,点 P 不在 ∠AOB 的内部 ( )
(3) 如图②, ∠ABC与∠DBE是同一个角 ( )
A
O
B
·
P
D
A
B
C
·
E
·
×
×
√
图① 图②
随堂演练
角与角的大小比较
角的概念及表示方法
角的大小比较
角平分线
叠合法
度量法
第4章 分式
4.3.1 角与角的大小比较
观察
如图,钟面上的时针和分针、圆规的两只脚之间、折扇的扇骨与扇骨之间都给我们以什么样的形象?
情景引入
这里有许多角……
角是由具有公共端点的两条射线组成的图形。
获取新知
观察角的图像,你能归纳出角的概念吗?尝试去描述一下角是由什么组成的图形?
获取新知
O
A
B
有公共端点的两条射线组成的图形叫做角. (静态定义)
始边
终边
一条射线绕着它的端点从一个位置旋转到另一位置时所成的图形叫做角. (动态定义)
公共端点
—-角的顶点
两条射线
—-角的边
角的内部
获取新知
其中,射线的端点O叫做角的顶点。射线原来所在的位置OA叫做角的始边,旋转后的位置OB叫做角的终边,角的始边和终边统称为角的边。从始边旋转到终边所扫过的区域,叫做角的内部。
角的大小由角的始边绕顶点旋转至终边时旋转的量的大小决定。
获取新知
O
A
B
O
A
(B)
平角
周角
O
A
B
(B)
平角的两边成一条直线.
周角的两边重合成一条射线.
当射线绕端点旋转到与原来的位置在同一直线上但方向相反时,所成的角叫做平角.
当射线绕端点旋转一周,又重新回到原来的位置时,所成的角叫做周角.
角通常可用如图所示的方法来表示.
获取新知
方法 图示 记法 适用范围
1.用三个大写字母表示 ∠AOB 或∠BOA 任何角
2.用一个大写字母表示 ∠O 顶点处只有一个角
3.用一个数字或希腊字母来表示 有弧线和数字
弧线和小写希腊字母
O
A
B
O
1
角的表示方法总结
获取新知
探究
怎样比较图中的∠ABC和∠DEF的大小?
可用量角器量
与线段长短的比较类似,可以把它们叠合在一起比较大小。
先将∠DEF移动,使它的顶点E与∠ABC的顶点B重合,并且使∠DEF的一条边EF与∠ABC的一条边BC重合,边ED,BA都在BC的同侧,这时可能出现的情形如下表:
获取新知
情形 图形 ∠ABC与∠DEF的关系
ED与BA重合 ∠ABC = ∠DEF
ED落在∠ABC内部 ∠ABC > ∠DEF
ED落在∠ABC外部 ∠ABC < ∠DEF
获取新知
以一个角的顶点为端点的一条射线,如果把这个角分成两个相等的角,那么这条射线叫做这个角的平分线。如图,若OC是∠AOB的平分线,则∠AOC=∠BOC=1/2∠AOB.
获取新知
1、 判断
(1) 直线是一个平角 ( )
(2) 如图①,点 P 不在 ∠AOB 的内部 ( )
(3) 如图②, ∠ABC与∠DBE是同一个角 ( )
A
O
B
·
P
D
A
B
C
·
E
·
×
×
√
图① 图②
随堂演练
角与角的大小比较
角的概念及表示方法
角的大小比较
角平分线
叠合法
度量法
同课章节目录
