湘教版七年级上册1.2.3绝对值课件(共16张PPT)
文档属性
| 名称 | 湘教版七年级上册1.2.3绝对值课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 297.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 23:36:11 | ||
图片预览




文档简介
(共16张PPT)
第1章 有理数
1.2 第3课时 绝对值
1、3到原点的距离是_____,-3到原点的距离是_____ ,到原点的距离是3的数是________.
2、3的相反数是_____,-3的相反数是_____,0的相反数是_____.
3
3
-3和3
-3
3
0
旧知回顾
如果两个数只有符号不同,那么其中一个数叫做另一个数的相反数。
0的相反数是0。
表示互为相反数的两个数的点,在数轴上分别位于原点的两侧,并且与原点的距离相等。
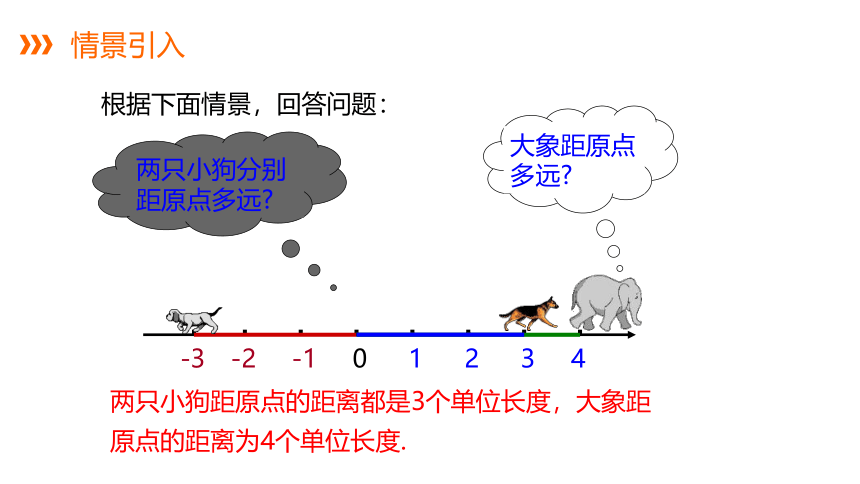
大象距原点多远
两只小狗分别距原点多远
0
1
2
3
4
-1
-2
-3
根据下面情景,回答问题:
两只小狗距原点的距离都是3个单位长度,大象距原点的距离为4个单位长度.
情景引入
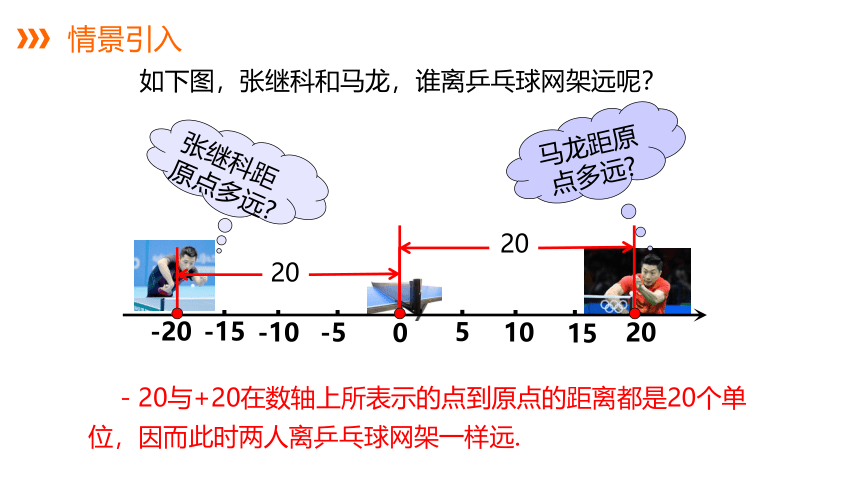
张继科距原点多远
20
20
马龙距原点多远
-20与+20在数轴上所表示的点到原点的距离都是20个单位,因而此时两人离乒乓球网架一样远.
0
5
10
15
20
-5
-10
-15
-20
如下图,张继科和马龙,谁离乒乓球网架远呢?
情景引入
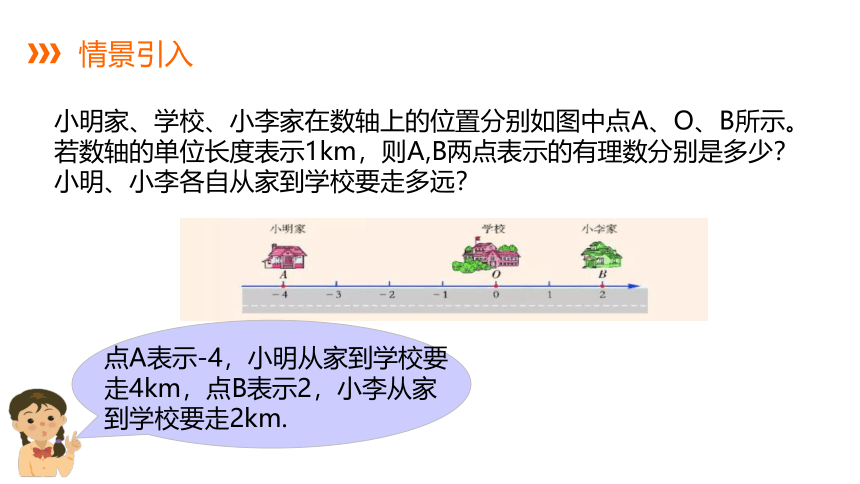
小明家、学校、小李家在数轴上的位置分别如图中点A、O、B所示。若数轴的单位长度表示1km,则A,B两点表示的有理数分别是多少?小明、小李各自从家到学校要走多远?
点A表示-4,小明从家到学校要走4km,点B表示2,小李从家到学校要走2km.
情景引入
我们把4叫做-4的绝对值,记做“|-4|=4”;把2叫做2的绝对值,记做“|2|=2.
一般的,数学上规定:
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0.
获取新知
从而,互为相反数的两个数的绝对值相等。
-4的绝对值等于数轴上表示-4的点A与原点之间的距离,2的绝对值等于数轴上表示2的点B与原点之间的距离。
一般地,有下述结论:
一个数的绝对值等于数轴上表示这个数的点与原点的距离。
获取新知
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
4到原点的距离是4,所以4的绝对值是4,记作|4|=4
-5到原点的距离是5,所以-5的绝对值是5,记作|-5|=5
数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|.互为相反数的绝对值相等.如-10和10的绝对值是10.
0到原点的距离是0,所以0的绝对值是0,记作|0|=0
获取新知
1.表示+7的点与原点的距离是 个单位长度,即+7的绝值是 ,记作 ;
2.表示2.8的点与原点的距离是 个单位长度,即2.8的绝对值是 ,记作 ;
3.表示0的点与原点的距离是 个单位长度,即0的绝对值是 ,记作 ;
4. 表示-6的点与原点的距离是 个单位长度,即-6的绝对值是____,记作 .
7
7
|7|
2.8
2.8
|2.8|
0
0
|0|
6
6
|-6|
随堂演练
例5
求下列各数的绝对值.
12, ,-7.5, 0.
解:
|12|=12;
| |= ;
|-7.5|=7.5;
|0|=0.
正数的绝对值等于它本身
负数的绝对值等于它的相反数
0的绝对值是0
例题讲解
一般地,如果a表示一个数,则
(1)当a是正数时,|a|=a
(2)当a是负数时,|a|=-a
(3)当 a=0,那么|a|=0
即|a| 是指a 和-a中非负数的那一个
如果a表示一个数,则|a|等于多少?
说一说
获取新知
若︱a︱=8.7,求a
解:因为绝对值等于8.7的有理数有8.7、-8.7两个,
所以a=8.7 或 a=-8.7
例题讲解
例6
任何一个数a的绝对值总是______的,即|a|_____0.
分情况而言:当a≠0时,|a|_____0;当a=0时,|a|_____.
归纳:
非负
≥
>
=0
1) 绝对值是7的数有几个?各是什么?有没有绝对值是-2的数?
答:绝对值是7的数有两个,各是7与-7.
没有绝对值是-2的数.
绝对值是0的数有几个?各是什么?
答:绝对值是0的数有一个,就是0.
3)绝对值小于3的整数一共有多少个?
答:绝对值小于3的整数一共有5个,
它们分别是-2,-1,0,1,2.
随堂演练
已知|x|=2,|y|=3,且x[解析] 由绝对值的定义知x=±2,y=±3,再由x解:因为|x|=2,|y|=3,
所以x=±2,y=±3.
又因为x所以x=2,y=3或x=-2,y=3.
例题讲解
一个正数的绝对值等于它本身
一个负数的绝对值等于它的相反数
0的绝对值等于0
互为相反数的两个数的绝对值相等
课堂小结
第1章 有理数
1.2 第3课时 绝对值
1、3到原点的距离是_____,-3到原点的距离是_____ ,到原点的距离是3的数是________.
2、3的相反数是_____,-3的相反数是_____,0的相反数是_____.
3
3
-3和3
-3
3
0
旧知回顾
如果两个数只有符号不同,那么其中一个数叫做另一个数的相反数。
0的相反数是0。
表示互为相反数的两个数的点,在数轴上分别位于原点的两侧,并且与原点的距离相等。
大象距原点多远
两只小狗分别距原点多远
0
1
2
3
4
-1
-2
-3
根据下面情景,回答问题:
两只小狗距原点的距离都是3个单位长度,大象距原点的距离为4个单位长度.
情景引入
张继科距原点多远
20
20
马龙距原点多远
-20与+20在数轴上所表示的点到原点的距离都是20个单位,因而此时两人离乒乓球网架一样远.
0
5
10
15
20
-5
-10
-15
-20
如下图,张继科和马龙,谁离乒乓球网架远呢?
情景引入
小明家、学校、小李家在数轴上的位置分别如图中点A、O、B所示。若数轴的单位长度表示1km,则A,B两点表示的有理数分别是多少?小明、小李各自从家到学校要走多远?
点A表示-4,小明从家到学校要走4km,点B表示2,小李从家到学校要走2km.
情景引入
我们把4叫做-4的绝对值,记做“|-4|=4”;把2叫做2的绝对值,记做“|2|=2.
一般的,数学上规定:
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0.
获取新知
从而,互为相反数的两个数的绝对值相等。
-4的绝对值等于数轴上表示-4的点A与原点之间的距离,2的绝对值等于数轴上表示2的点B与原点之间的距离。
一般地,有下述结论:
一个数的绝对值等于数轴上表示这个数的点与原点的距离。
获取新知
0
6
-1
-2
-3
-4
-5
-6
1
2
3
4
5
4到原点的距离是4,所以4的绝对值是4,记作|4|=4
-5到原点的距离是5,所以-5的绝对值是5,记作|-5|=5
数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|.互为相反数的绝对值相等.如-10和10的绝对值是10.
0到原点的距离是0,所以0的绝对值是0,记作|0|=0
获取新知
1.表示+7的点与原点的距离是 个单位长度,即+7的绝值是 ,记作 ;
2.表示2.8的点与原点的距离是 个单位长度,即2.8的绝对值是 ,记作 ;
3.表示0的点与原点的距离是 个单位长度,即0的绝对值是 ,记作 ;
4. 表示-6的点与原点的距离是 个单位长度,即-6的绝对值是____,记作 .
7
7
|7|
2.8
2.8
|2.8|
0
0
|0|
6
6
|-6|
随堂演练
例5
求下列各数的绝对值.
12, ,-7.5, 0.
解:
|12|=12;
| |= ;
|-7.5|=7.5;
|0|=0.
正数的绝对值等于它本身
负数的绝对值等于它的相反数
0的绝对值是0
例题讲解
一般地,如果a表示一个数,则
(1)当a是正数时,|a|=a
(2)当a是负数时,|a|=-a
(3)当 a=0,那么|a|=0
即|a| 是指a 和-a中非负数的那一个
如果a表示一个数,则|a|等于多少?
说一说
获取新知
若︱a︱=8.7,求a
解:因为绝对值等于8.7的有理数有8.7、-8.7两个,
所以a=8.7 或 a=-8.7
例题讲解
例6
任何一个数a的绝对值总是______的,即|a|_____0.
分情况而言:当a≠0时,|a|_____0;当a=0时,|a|_____.
归纳:
非负
≥
>
=0
1) 绝对值是7的数有几个?各是什么?有没有绝对值是-2的数?
答:绝对值是7的数有两个,各是7与-7.
没有绝对值是-2的数.
绝对值是0的数有几个?各是什么?
答:绝对值是0的数有一个,就是0.
3)绝对值小于3的整数一共有多少个?
答:绝对值小于3的整数一共有5个,
它们分别是-2,-1,0,1,2.
随堂演练
已知|x|=2,|y|=3,且x
所以x=±2,y=±3.
又因为x
例题讲解
一个正数的绝对值等于它本身
一个负数的绝对值等于它的相反数
0的绝对值等于0
互为相反数的两个数的绝对值相等
课堂小结
同课章节目录
