湘教版七年级上册1.2.2 相反数课件(共18张PPT)
文档属性
| 名称 | 湘教版七年级上册1.2.2 相反数课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 336.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
第1章 有理数
1.2 第2课时 相反数
正方向
数轴的三要素
单位长度
原点
旧知回顾
数轴的引入,使我们能用直观图形来理解数的有关概念,这就是“数”与“形”的结合,数形结合是一种重要的方法,我们应注意掌握。
1、填空:
数轴上表示-2的点在原点的 侧,距原
点的距离是 ,表示6的点在原点的 侧,距原点的距离是 。
6个单位
左
右
2个单位
2、判断
数轴上的两个点可以表示同一个有理数( )
╳
旧知回顾
3、画一条数轴,标出表示下列各数的点.
1,-1,0,3,-3.
解:
旧知回顾
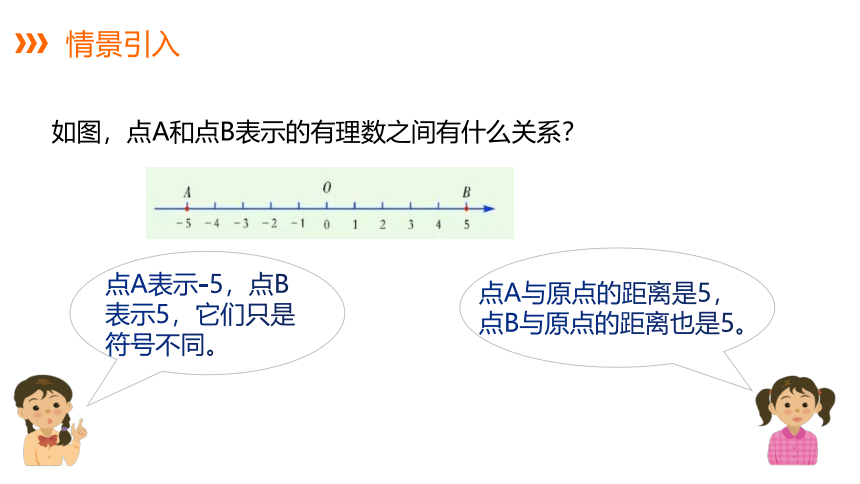
情景引入
如图,点A和点B表示的有理数之间有什么关系?
点A表示-5,点B表示5,它们只是符号不同。
点A与原点的距离是5,点B与原点的距离也是5。
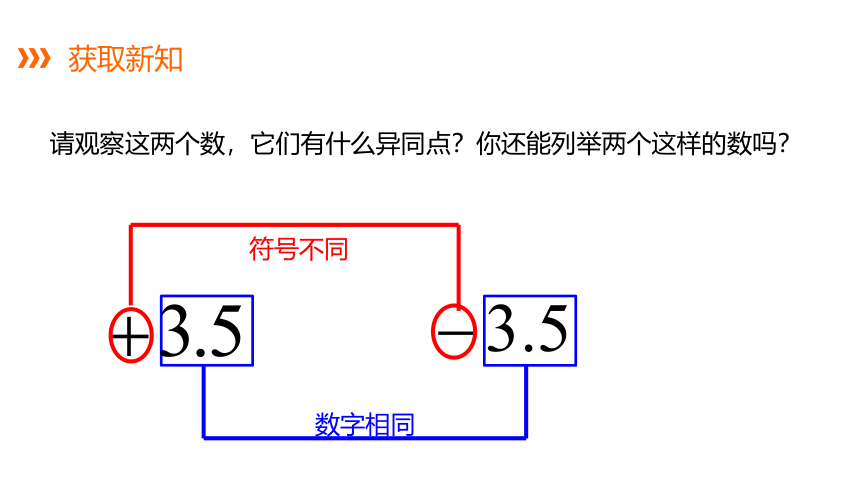
请观察这两个数,它们有什么异同点?你还能列举两个这样的数吗?
数字相同
符号不同
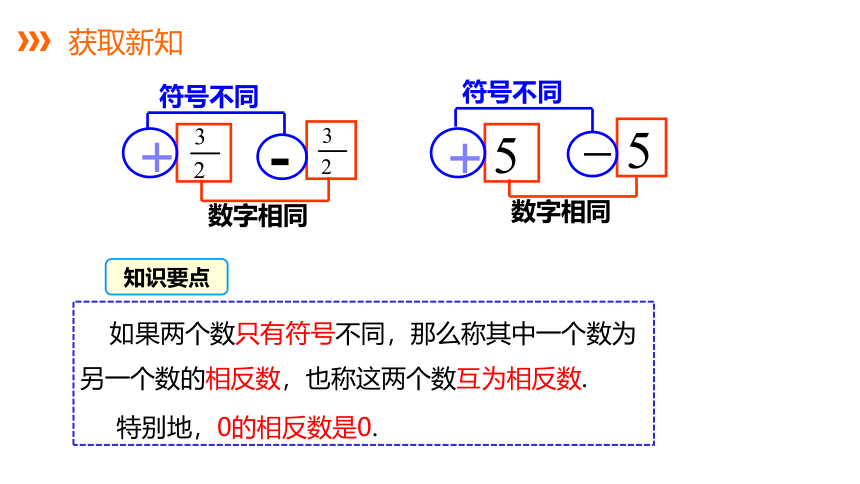
获取新知
如果两个数只有符号不同,那么称其中一个数为另一个数的相反数,也称这两个数互为相反数.
特别地,0的相反数是0.
数字相同
符号不同
+
-
数字相同
符号不同
+
知识要点
获取新知
1.代数意义:如果两个数_______________,那么其中一个数叫做另一个数的相反数.数a的相反数记作_____.特别地,0的相反数是_____.
2.几何意义:表示互为相反数的两个点,在数轴上分别位于原点的____,并且与原点的____相等.
3.-a表示a的______.因此,在这个数的前面添上“-”号,就得到这个数的______.正数的“+”号可省略不写,因此,在一个数前面添上“+”号,表示这个数____.
4.正数的相反数是____,负数的相反数是____,0的相反数是____.
归纳:
只有符号不同
-a
0
两侧
距离
相反数
相反数
本身
负数
正数
0
获取新知
例3 画一条数轴,并标出表示下列各数的相反数的点:
3,1.5,-6
解:3的相反数是-3,;1.5的相反数是-1.5;-6的相反数是6,且-3,-1.5,6在数轴上对应的点分别为A,B,C,如下图所示:
-4 -3 -2 -1 0 1 2 3 4 5 6
A
B
C
例题讲解
思考:a的相反数是什么?
a 的相反数是-a , a可表示任意有理数.
在一个数前面加上“-”号表示求这个数的相反数,如果在这些数前面加上“+”号呢?
在一个数前面加上“+”仍表示这个数,“+”号可省略.
获取新知
说一说:
-(+1)= -(-1)=
因为+1的相反数是-1,所以-(+1)=-1。
因为-1的相反数是1,所以-(-1)=1
获取新知
填空
-(+0.8)=_______ ; -(-3)=_______
解: -(+0.8)= -08; -(-3)=3
例4
例题讲解
练习
下面两个数互为相反数的是( )
D.π和-3.14
C
随堂演练
注意:
(1)相反数是成对出现的,它们不能单独存在;
(2)“只有符号不同”指的是仅仅是符号不同,而数字应该是相同的(或能化得相同).
提示:
数a的相反数是-a,记作-(a)=-a;
-a的相反数是a,记作-(-a)=a.
这里a可表示正数,负数和0.
1、化简下列各数:
(1)-(+10); (2)+(-0.15); (3)+(+3);
(4)-(-12); (5)+[-(-1.1)] ;(6)-[+(-7)].
解:(1)-(+10)=-10;
(2)+(-0.15)=-0.15;
(3)+(+3)=3;
(4)-(-12)=12;
(5)+[-(-1.1)]=+(+1.1)=1.1;
(6)-[+(-7)]=-(-7)=7.
由内向外依次去括号
随堂演练
对于数字前面含有多个符号的数的化简,只要观察“-”号的个数即可.如果有奇数个“-”号,结果的符号就是“-”号;如果有偶数个“-”号,结果的符号就是“+”号.
方法总结
随堂演练
练习
填空:
-(+3)=_____; -(-3)= _____ ;
+(-3)=_____ ; -0= _____ .
-3
-3
3
0
课堂小结
相反数
定义
应用
只有符号不同的两个数互为相反数;
0的相反数是0
代数意义
几何意义
数a的相反数是-a
两个互为相反数的数在数轴上所表示的点在原点的两旁,且与原点的距离相等
求某数的相反数
化简:-(-a)= a
如果a 表示有理数,那么a的相反数是-a ,-a一定是负数吗?
注意
解:不一定,可以是正数、负数,也可以是0.
第1章 有理数
1.2 第2课时 相反数
正方向
数轴的三要素
单位长度
原点
旧知回顾
数轴的引入,使我们能用直观图形来理解数的有关概念,这就是“数”与“形”的结合,数形结合是一种重要的方法,我们应注意掌握。
1、填空:
数轴上表示-2的点在原点的 侧,距原
点的距离是 ,表示6的点在原点的 侧,距原点的距离是 。
6个单位
左
右
2个单位
2、判断
数轴上的两个点可以表示同一个有理数( )
╳
旧知回顾
3、画一条数轴,标出表示下列各数的点.
1,-1,0,3,-3.
解:
旧知回顾
情景引入
如图,点A和点B表示的有理数之间有什么关系?
点A表示-5,点B表示5,它们只是符号不同。
点A与原点的距离是5,点B与原点的距离也是5。
请观察这两个数,它们有什么异同点?你还能列举两个这样的数吗?
数字相同
符号不同
获取新知
如果两个数只有符号不同,那么称其中一个数为另一个数的相反数,也称这两个数互为相反数.
特别地,0的相反数是0.
数字相同
符号不同
+
-
数字相同
符号不同
+
知识要点
获取新知
1.代数意义:如果两个数_______________,那么其中一个数叫做另一个数的相反数.数a的相反数记作_____.特别地,0的相反数是_____.
2.几何意义:表示互为相反数的两个点,在数轴上分别位于原点的____,并且与原点的____相等.
3.-a表示a的______.因此,在这个数的前面添上“-”号,就得到这个数的______.正数的“+”号可省略不写,因此,在一个数前面添上“+”号,表示这个数____.
4.正数的相反数是____,负数的相反数是____,0的相反数是____.
归纳:
只有符号不同
-a
0
两侧
距离
相反数
相反数
本身
负数
正数
0
获取新知
例3 画一条数轴,并标出表示下列各数的相反数的点:
3,1.5,-6
解:3的相反数是-3,;1.5的相反数是-1.5;-6的相反数是6,且-3,-1.5,6在数轴上对应的点分别为A,B,C,如下图所示:
-4 -3 -2 -1 0 1 2 3 4 5 6
A
B
C
例题讲解
思考:a的相反数是什么?
a 的相反数是-a , a可表示任意有理数.
在一个数前面加上“-”号表示求这个数的相反数,如果在这些数前面加上“+”号呢?
在一个数前面加上“+”仍表示这个数,“+”号可省略.
获取新知
说一说:
-(+1)= -(-1)=
因为+1的相反数是-1,所以-(+1)=-1。
因为-1的相反数是1,所以-(-1)=1
获取新知
填空
-(+0.8)=_______ ; -(-3)=_______
解: -(+0.8)= -08; -(-3)=3
例4
例题讲解
练习
下面两个数互为相反数的是( )
D.π和-3.14
C
随堂演练
注意:
(1)相反数是成对出现的,它们不能单独存在;
(2)“只有符号不同”指的是仅仅是符号不同,而数字应该是相同的(或能化得相同).
提示:
数a的相反数是-a,记作-(a)=-a;
-a的相反数是a,记作-(-a)=a.
这里a可表示正数,负数和0.
1、化简下列各数:
(1)-(+10); (2)+(-0.15); (3)+(+3);
(4)-(-12); (5)+[-(-1.1)] ;(6)-[+(-7)].
解:(1)-(+10)=-10;
(2)+(-0.15)=-0.15;
(3)+(+3)=3;
(4)-(-12)=12;
(5)+[-(-1.1)]=+(+1.1)=1.1;
(6)-[+(-7)]=-(-7)=7.
由内向外依次去括号
随堂演练
对于数字前面含有多个符号的数的化简,只要观察“-”号的个数即可.如果有奇数个“-”号,结果的符号就是“-”号;如果有偶数个“-”号,结果的符号就是“+”号.
方法总结
随堂演练
练习
填空:
-(+3)=_____; -(-3)= _____ ;
+(-3)=_____ ; -0= _____ .
-3
-3
3
0
课堂小结
相反数
定义
应用
只有符号不同的两个数互为相反数;
0的相反数是0
代数意义
几何意义
数a的相反数是-a
两个互为相反数的数在数轴上所表示的点在原点的两旁,且与原点的距离相等
求某数的相反数
化简:-(-a)= a
如果a 表示有理数,那么a的相反数是-a ,-a一定是负数吗?
注意
解:不一定,可以是正数、负数,也可以是0.
同课章节目录
