探索勾股定理
图片预览


文档简介
课件26张PPT。
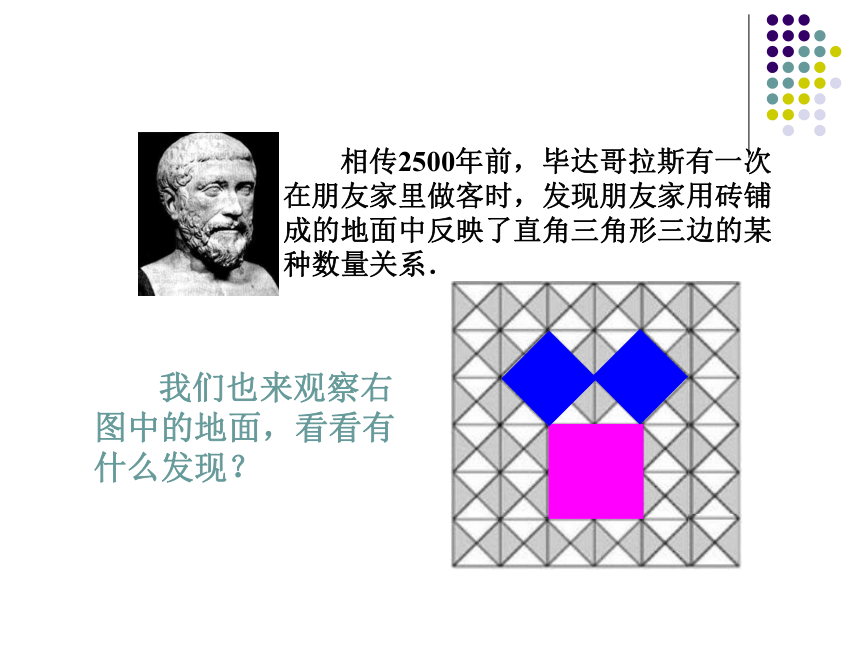
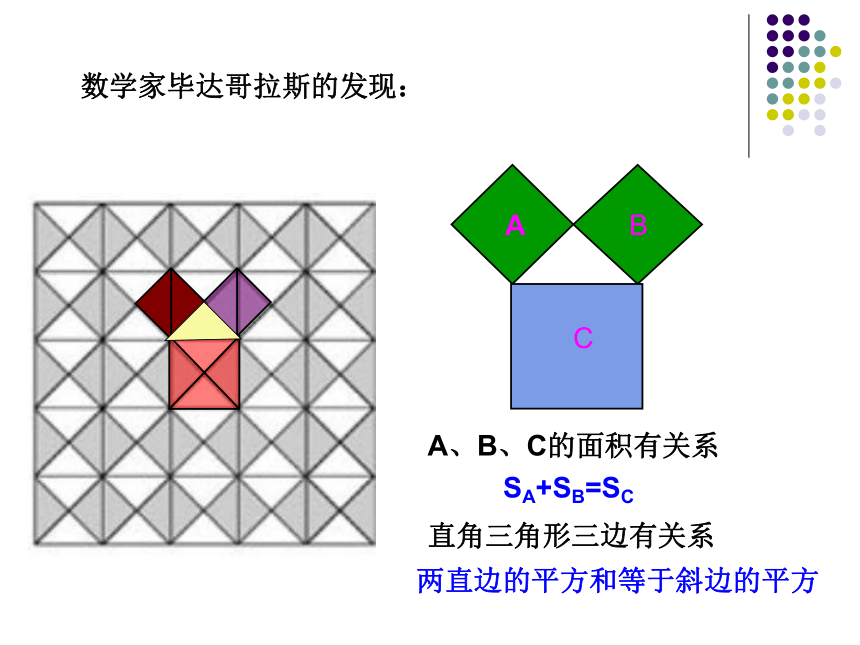
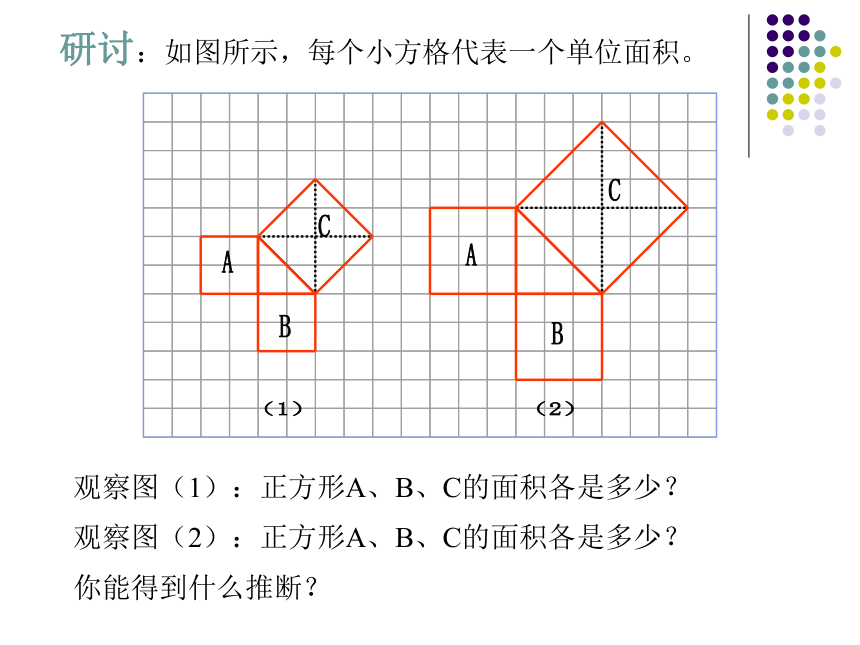
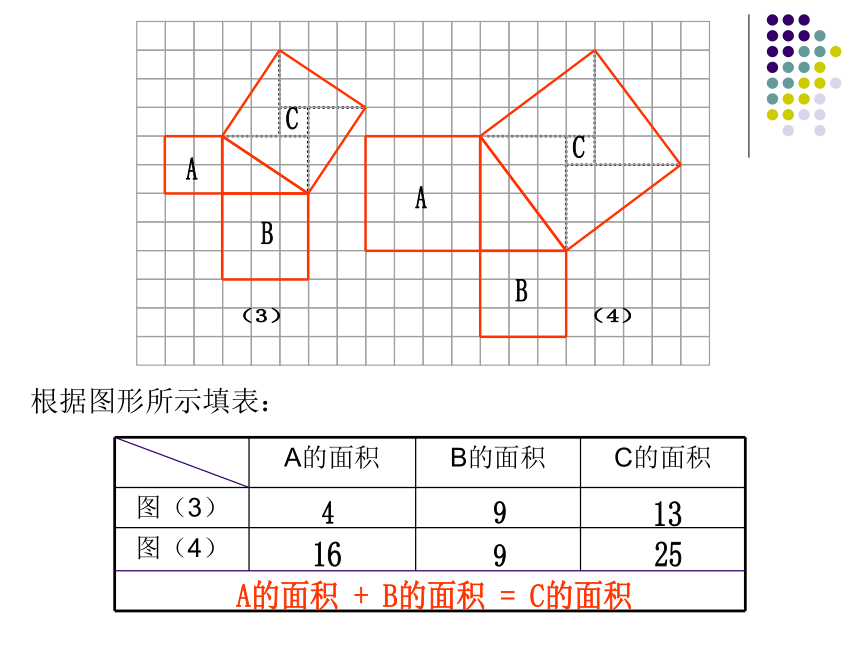
???是否有外星人存在?如果有的话,我们 怎么样才能与”外星人”接触呢? 数学家曾建议用“勾股定理”图作为与“外星人”联系的信号。这就是本届大会会徽的图案.你见过这个图案吗?你听说过勾股定理吗? 这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”. 探索勾股定理 相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系. 我们也来观察右图中的地面,看看有什么发现? 数学家毕达哥拉斯的发现:A、B、C的面积有关系直角三角形三边有关系SA+SB=SC两直边的平方和等于斜边的平方研讨:如图所示,每个小方格代表一个单位面积。观察图(1):正方形A、B、C的面积各是多少?观察图(2):正方形A、B、C的面积各是多少?你能得到什么推断?根据图形所示填表:A的面积 + B的面积 = C的面积练习:
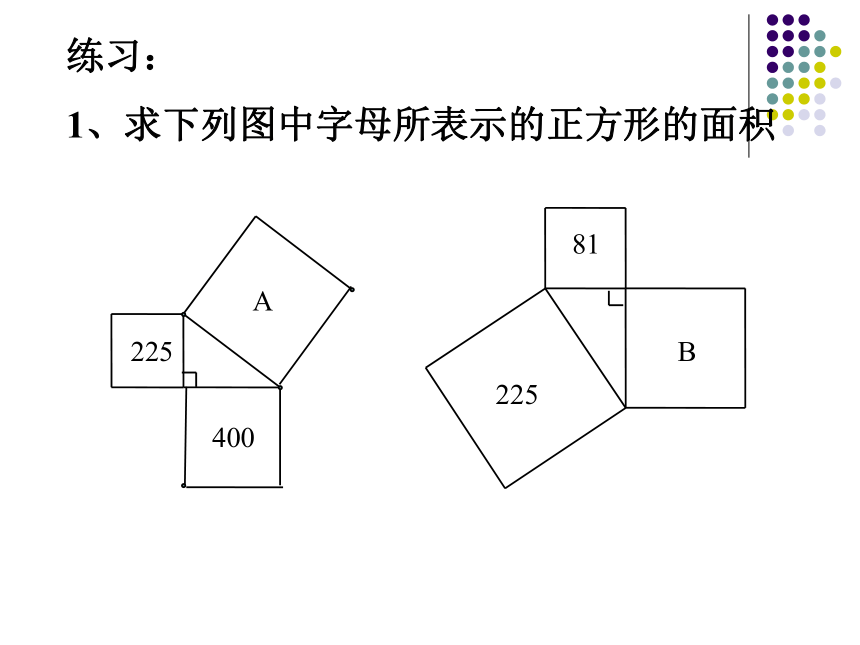
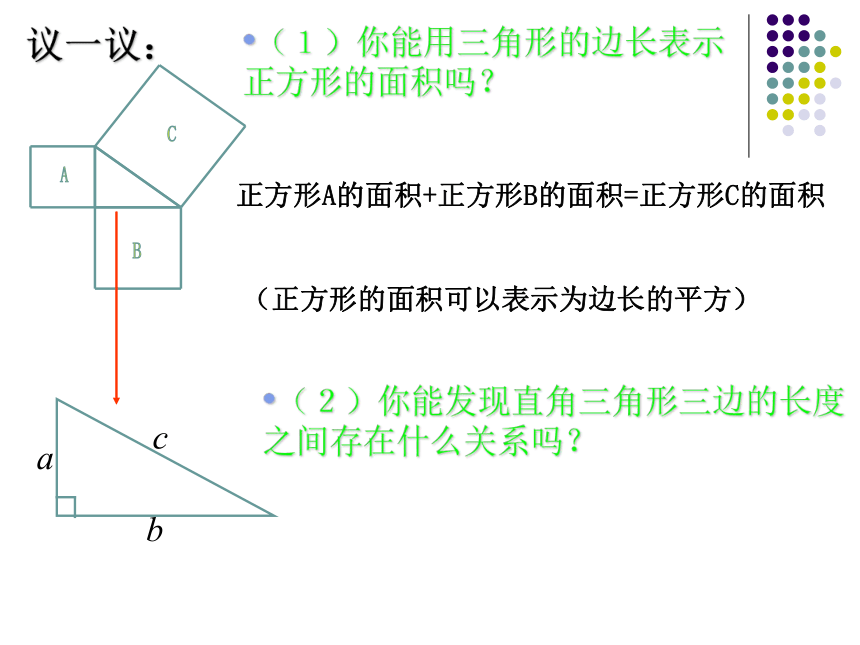
1、求下列图中字母所表示的正方形的面积正方形A的面积+正方形B的面积=正方形C的面积(正方形的面积可以表示为边长的平方)议一议:(1)你能用三角形的边长表示正方形的面积吗?(2)你能发现直角三角形三边的长度之间存在什么关系吗?做一做:1。分别以3厘米,4厘米为直角边作出一个直角三角形,并测量斜边的长度.看上面规律对这个三角形仍然成立吗?小结如果直角三角形的两直角边分别为a,b ,斜边为c,那么一、利用拼图来验证勾股定理:1、准备四个全等的直角三角形(设直角三角形的两条直角边分别为a,b,斜边c);2、你能用这四个直角三角形拼成一个正方形吗?拼一拼试试看3、你拼的正方形中是否含有以斜边c为边的正方形?4、你能否就你拼出的图说明a2+b2=c2?=2ab+b2-2ab+a2 =a2+b2∴a2+b2=c2大正方形的面积可以表示为 ;
也可以表示为c24? +(b- a)2
∵ c2= 4? +(b-a)2 ∵ (a+b)2 = c2 + 4?ab/2a2+2ab+b2 = c2 +2ab∴a2+b2=c2大正方形的面积可以表示为 ;
也可以表示为(a+b)2c2 +4?ab/2(2)美国总统证法:∴a2+b2 =c2 勾股定理(gou-gu theorem)如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。勾股弦(2)使用前提是直角三角形(3)分清直角边、斜边返回综合探究 例1.在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.解: (1)
(2)
(3)
(4)设a=3x,则b=4x,
所以5x=15
得x=3
所以a=9,b=12尝试应用2、一个门框尺寸如图18.1-2所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么? 在RtΔABC中,根据勾股定理:
AC2=AB2+BC2=12+22=5
所以,AC= ≈2.236
而AC大于木板的宽,所以木板能从门框内通过。1.判断题:(1).如果三角形的三边长分别为a,b,c,则
( )
(2).如果直角三角形的三边长分别为a,b,c,
( )
则
2.求出下列直角三角形中未知边的长度3.填空:(1).在△ABC中, ∠C=90°,c=25,b=15,则a=____.
(2). 三角形的三个内角之比为:1:2:3,则此三角形是___.若此三角形的三边长分别为a,b,c,则它们的关系是____.
问题:在第(2)题中,如果把 1:2:3改成3:2:1,答案会一样吗?
4.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。49回忆与小结:1、这节课你的收获是什么?
2、理解“勾股定理”应该注意什么?
3、你觉的“勾股定理”有用吗?作业:P69---70 1、2、3。 课中探究如图,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?在Rt△AOB中,
OB2= ,OB= .
在Rt△COD中,
OD2= ,OD= .
BD= .
梯子的顶端沿墙下滑0.5 m,梯子底端外移____再见!
???是否有外星人存在?如果有的话,我们 怎么样才能与”外星人”接触呢? 数学家曾建议用“勾股定理”图作为与“外星人”联系的信号。这就是本届大会会徽的图案.你见过这个图案吗?你听说过勾股定理吗? 这个图案是我国汉代数学家赵爽在证明勾股定理时用到的,被称为“赵爽弦图”. 探索勾股定理 相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系. 我们也来观察右图中的地面,看看有什么发现? 数学家毕达哥拉斯的发现:A、B、C的面积有关系直角三角形三边有关系SA+SB=SC两直边的平方和等于斜边的平方研讨:如图所示,每个小方格代表一个单位面积。观察图(1):正方形A、B、C的面积各是多少?观察图(2):正方形A、B、C的面积各是多少?你能得到什么推断?根据图形所示填表:A的面积 + B的面积 = C的面积练习:
1、求下列图中字母所表示的正方形的面积正方形A的面积+正方形B的面积=正方形C的面积(正方形的面积可以表示为边长的平方)议一议:(1)你能用三角形的边长表示正方形的面积吗?(2)你能发现直角三角形三边的长度之间存在什么关系吗?做一做:1。分别以3厘米,4厘米为直角边作出一个直角三角形,并测量斜边的长度.看上面规律对这个三角形仍然成立吗?小结如果直角三角形的两直角边分别为a,b ,斜边为c,那么一、利用拼图来验证勾股定理:1、准备四个全等的直角三角形(设直角三角形的两条直角边分别为a,b,斜边c);2、你能用这四个直角三角形拼成一个正方形吗?拼一拼试试看3、你拼的正方形中是否含有以斜边c为边的正方形?4、你能否就你拼出的图说明a2+b2=c2?=2ab+b2-2ab+a2 =a2+b2∴a2+b2=c2大正方形的面积可以表示为 ;
也可以表示为c24? +(b- a)2
∵ c2= 4? +(b-a)2 ∵ (a+b)2 = c2 + 4?ab/2a2+2ab+b2 = c2 +2ab∴a2+b2=c2大正方形的面积可以表示为 ;
也可以表示为(a+b)2c2 +4?ab/2(2)美国总统证法:∴a2+b2 =c2 勾股定理(gou-gu theorem)如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。勾股弦(2)使用前提是直角三角形(3)分清直角边、斜边返回综合探究 例1.在Rt△ABC中,∠C=90°.
(1) 已知:a=6,b=8,求c;
(2) 已知:a=40,c=41,求b;
(3) 已知:c=13,b=5,求a;
(4) 已知: a:b=3:4, c=15,求a、b.解: (1)
(2)
(3)
(4)设a=3x,则b=4x,
所以5x=15
得x=3
所以a=9,b=12尝试应用2、一个门框尺寸如图18.1-2所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么? 在RtΔABC中,根据勾股定理:
AC2=AB2+BC2=12+22=5
所以,AC= ≈2.236
而AC大于木板的宽,所以木板能从门框内通过。1.判断题:(1).如果三角形的三边长分别为a,b,c,则
( )
(2).如果直角三角形的三边长分别为a,b,c,
( )
则
2.求出下列直角三角形中未知边的长度3.填空:(1).在△ABC中, ∠C=90°,c=25,b=15,则a=____.
(2). 三角形的三个内角之比为:1:2:3,则此三角形是___.若此三角形的三边长分别为a,b,c,则它们的关系是____.
问题:在第(2)题中,如果把 1:2:3改成3:2:1,答案会一样吗?
4.如图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为7cm,则
正方形A,B,C,D的面积之和为___________cm2。49回忆与小结:1、这节课你的收获是什么?
2、理解“勾股定理”应该注意什么?
3、你觉的“勾股定理”有用吗?作业:P69---70 1、2、3。 课中探究如图,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?在Rt△AOB中,
OB2= ,OB= .
在Rt△COD中,
OD2= ,OD= .
BD= .
梯子的顶端沿墙下滑0.5 m,梯子底端外移____再见!
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
