北师大版七年级下册 1.1 同底数幂的乘法课件(共30张PPT)
文档属性
| 名称 | 北师大版七年级下册 1.1 同底数幂的乘法课件(共30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 424.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 23:50:29 | ||
图片预览











文档简介
(共31张PPT)
1.1 同底数幂的乘法
第一章 整式的乘除
1、2×2 ×2=2( )
2、a·a·a·a·a = a( )
3、a · a · · · · · · a = a( )
n个
3
5
n
①什么叫乘方
②乘方的结果叫做什么
知识回顾
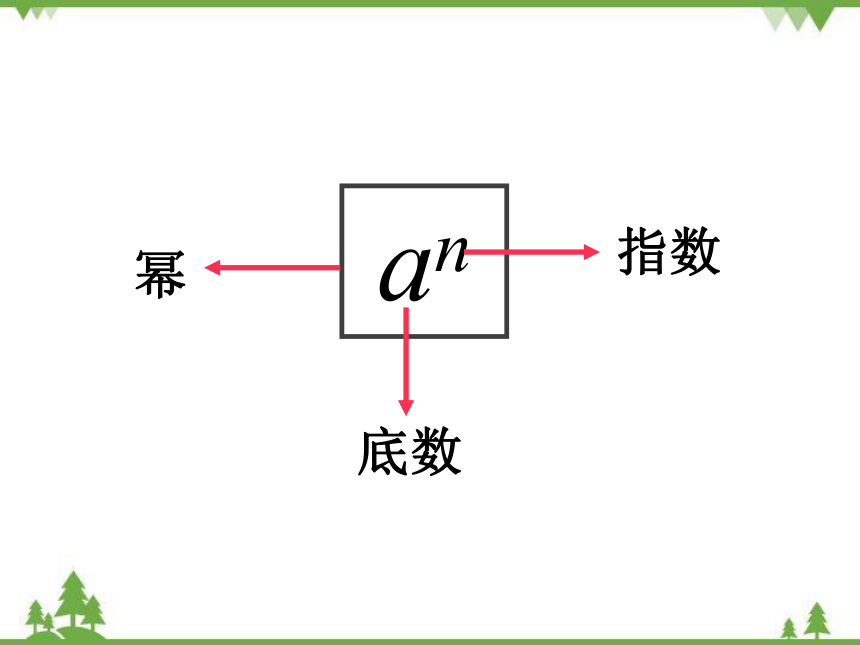
an
指数
幂
底数
说出an的乘法意义,并将下列各式写成乘法形式:
(1) 108
(2) (-2)4
=10×10×10×10×10×10×10×10
=(-2)×(-2)×(-2)×(-2)
(3) an = a × a × a ×… a
n个a
学习目标
1.经历探索同底数幂乘法的推理过程,进一步体会幂的意义,培养推理能力和有条理的表达能力,培养学生转化的数学思想.
2.掌握同底数幂的乘法法则,并运用同底数幂法则运算,解决实际问题.
一年以3×10 秒计算,比邻星与地球的距离约为多少?
7
问题:光在真空中的速度大约是3×10 m/s,
太阳系以外距离地球最近的恒星是比邻星,它发出
的光到达地球大约需要4.22年。
8
3×108×3×107×4.22=37.98×(108×107)
108×107结果等于多少?
问题引入
做一做
1、计算下列各式:
(1)102×103
(2)105×108
(3)10m×10n(m,n都是正整数).
你发现了什么?
=(10×10)×(10×10×10)
=10×10×10×10×10
=105
102 × 103
(1)
(根据 )
(根据 )
(根据 )
乘法结合律
幂的意义
幂的意义
=102+3
=(10×10×···×10)×(10×10×···×10)
5个10
8个10
=10×10×···×10
13个10
=10
13
幂的意义
乘法结合律
(根据 )
根据( )
根据( )
幂的意义
(2)
=105+8
=(10×10×···×10)×(10×10×···×10)
m个10
n个10
=10×10×···×10
(m+n)个10
=10
m+n
幂的意义
乘法结合律
(根据 )
根据( )
(根据 )
幂的意义
10 × 10
m
n
(3)
2. 2m×2n等于什么?
3. 和(-3)m×(-3)n呢?
(m,n都是正整数)
=2m+n
2m×2n
2.
n个2
=(2×2×···×2)×(2×2×···×2)
m个2
(-3)m×(- 3)n= (-3)m+n
类似地,得
猜想: am · an= (当m、n都是正整数)
分组讨论,并尝试证明你的猜想
是否正确。
am · an =
m个a
n个a
= aa…a
=am+n
(m+n)个a
即
am · an = am+n (当m、n都是正整数)
(aa…a).
(aa…a)
(乘方的意义)
(乘法结合律)
(乘方的意义)
am · an = am+n (当m、n都是正整数)
同底数幂相乘,
底数_____,指数_____。
不变
相加
同底数幂的乘法公式:
如 43×45=
43+5
=48
运算形式
运算方法
(同底、乘法)
(底不变、指数相加)
幂的底数必须相同,
相乘时指数才能相加.
例1:计算
(1)(-3)7×(-3)6
(2)
(3)-x3 · x5
(4)b2m· b2m+1
=(-3)13
=-x8
=b4m+1
想一想
am · an · ap 等于什么?
am· an· ap = am+n+p
方法1 am·an·ap
=(am·an)·ap
=am+n·ap
=am+n+p
am·an·ap
=am ·(an·ap )
=am·ap +n
=am+n+p
或
方法2 am·an·ap
=(a·a· … ·a)(a·a· … ·a)(a·a· … ·a)
n个a
m个a
p个a
=am+n+p
例2 光在真空中的速度约为3×108m/s,太阳光照射到地球大约需要5×102s. 地球距离太阳大约有多远?
解:3×108×5×102
=15×1010
=1.5×1011(m)
地球距离太阳大约有1.5×1011m.
练习一
( 710 )
( a15 )
( x8 )
( b6 )
(2) a7 ·a8
(3) x5 ·x3
(4) b5 · b
(1) 76×74
1. 计算:(抢答)
2. 计算:
(1)x10 · x (2)10×102×104
(3)x5 ·x ·x3 (4)y4·y3·y2·y
解:
(1)x10 ·x = x10+1= x11
(2)10×102×104 =101+2+4 =107
(3)x5 ·x ·x3 = x5+1+3 = x9
(4)y4 ·y3 ·y2 ·y= y4+3+2+1= y10
下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x2 = x10 ( ) (4)y5 +2 y5 =3y10 ( )
(5)c · c3 = c3 ( ) (6)m + m3 = m4 ( )
m + m3 = m + m3
b5 · b5= b10
b5 + b5 = 2b5
x5 · x2 = x7
y5 + 2 y5 =3y5
c · c3 = c4
×
×
×
×
×
×
练习二
练习提高
(1) x n · xn+1
(2) (x+y)3 · (x+y)4
1.计算:
解:
x n · xn+1 =
解:
(x+y)3 · (x+y)4 =
am · an = am+n
xn+(n+1)
= x2n+1
公式中的a可代表一个数、字母、式子等。
(x+y)3+4 =(x+y)7
2.填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = 。
3
5
6
23
23
3
25
36
22
×
=
33
32
×
×
=
3 .计算
(1)(-2)3×(-2)5
(2) (-2)2×(-2)7
(3) (-2)3×25
(4) (-2)2×27
(5)(x)2(-x)3(-x)
(6)32×3×9 - 3×34
=28
=-29
=-28
=29
=x6
=0
已知:am=2,an=3.求am+n =?
拓展延伸
解: am+n =
am · an
=2 × 3
=6
(2)已知:an-3×a2n+1=a10,则n=_______
(3)如果2n=2,2m=8,则3n×3m =____.
4
81
(1)已知x =2,x =3,求x _______
a
b
a+b
6
能力提高
小结感悟
1. 对自己说,你有什么收获?
2. 对同学说,你有什么温馨提示?
3. 对老师说,你还有什么困惑?
布置作业,强化目标
作业:习题1.1
1.1 同底数幂的乘法
第一章 整式的乘除
1、2×2 ×2=2( )
2、a·a·a·a·a = a( )
3、a · a · · · · · · a = a( )
n个
3
5
n
①什么叫乘方
②乘方的结果叫做什么
知识回顾
an
指数
幂
底数
说出an的乘法意义,并将下列各式写成乘法形式:
(1) 108
(2) (-2)4
=10×10×10×10×10×10×10×10
=(-2)×(-2)×(-2)×(-2)
(3) an = a × a × a ×… a
n个a
学习目标
1.经历探索同底数幂乘法的推理过程,进一步体会幂的意义,培养推理能力和有条理的表达能力,培养学生转化的数学思想.
2.掌握同底数幂的乘法法则,并运用同底数幂法则运算,解决实际问题.
一年以3×10 秒计算,比邻星与地球的距离约为多少?
7
问题:光在真空中的速度大约是3×10 m/s,
太阳系以外距离地球最近的恒星是比邻星,它发出
的光到达地球大约需要4.22年。
8
3×108×3×107×4.22=37.98×(108×107)
108×107结果等于多少?
问题引入
做一做
1、计算下列各式:
(1)102×103
(2)105×108
(3)10m×10n(m,n都是正整数).
你发现了什么?
=(10×10)×(10×10×10)
=10×10×10×10×10
=105
102 × 103
(1)
(根据 )
(根据 )
(根据 )
乘法结合律
幂的意义
幂的意义
=102+3
=(10×10×···×10)×(10×10×···×10)
5个10
8个10
=10×10×···×10
13个10
=10
13
幂的意义
乘法结合律
(根据 )
根据( )
根据( )
幂的意义
(2)
=105+8
=(10×10×···×10)×(10×10×···×10)
m个10
n个10
=10×10×···×10
(m+n)个10
=10
m+n
幂的意义
乘法结合律
(根据 )
根据( )
(根据 )
幂的意义
10 × 10
m
n
(3)
2. 2m×2n等于什么?
3. 和(-3)m×(-3)n呢?
(m,n都是正整数)
=2m+n
2m×2n
2.
n个2
=(2×2×···×2)×(2×2×···×2)
m个2
(-3)m×(- 3)n= (-3)m+n
类似地,得
猜想: am · an= (当m、n都是正整数)
分组讨论,并尝试证明你的猜想
是否正确。
am · an =
m个a
n个a
= aa…a
=am+n
(m+n)个a
即
am · an = am+n (当m、n都是正整数)
(aa…a).
(aa…a)
(乘方的意义)
(乘法结合律)
(乘方的意义)
am · an = am+n (当m、n都是正整数)
同底数幂相乘,
底数_____,指数_____。
不变
相加
同底数幂的乘法公式:
如 43×45=
43+5
=48
运算形式
运算方法
(同底、乘法)
(底不变、指数相加)
幂的底数必须相同,
相乘时指数才能相加.
例1:计算
(1)(-3)7×(-3)6
(2)
(3)-x3 · x5
(4)b2m· b2m+1
=(-3)13
=-x8
=b4m+1
想一想
am · an · ap 等于什么?
am· an· ap = am+n+p
方法1 am·an·ap
=(am·an)·ap
=am+n·ap
=am+n+p
am·an·ap
=am ·(an·ap )
=am·ap +n
=am+n+p
或
方法2 am·an·ap
=(a·a· … ·a)(a·a· … ·a)(a·a· … ·a)
n个a
m个a
p个a
=am+n+p
例2 光在真空中的速度约为3×108m/s,太阳光照射到地球大约需要5×102s. 地球距离太阳大约有多远?
解:3×108×5×102
=15×1010
=1.5×1011(m)
地球距离太阳大约有1.5×1011m.
练习一
( 710 )
( a15 )
( x8 )
( b6 )
(2) a7 ·a8
(3) x5 ·x3
(4) b5 · b
(1) 76×74
1. 计算:(抢答)
2. 计算:
(1)x10 · x (2)10×102×104
(3)x5 ·x ·x3 (4)y4·y3·y2·y
解:
(1)x10 ·x = x10+1= x11
(2)10×102×104 =101+2+4 =107
(3)x5 ·x ·x3 = x5+1+3 = x9
(4)y4 ·y3 ·y2 ·y= y4+3+2+1= y10
下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x2 = x10 ( ) (4)y5 +2 y5 =3y10 ( )
(5)c · c3 = c3 ( ) (6)m + m3 = m4 ( )
m + m3 = m + m3
b5 · b5= b10
b5 + b5 = 2b5
x5 · x2 = x7
y5 + 2 y5 =3y5
c · c3 = c4
×
×
×
×
×
×
练习二
练习提高
(1) x n · xn+1
(2) (x+y)3 · (x+y)4
1.计算:
解:
x n · xn+1 =
解:
(x+y)3 · (x+y)4 =
am · an = am+n
xn+(n+1)
= x2n+1
公式中的a可代表一个数、字母、式子等。
(x+y)3+4 =(x+y)7
2.填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = 。
3
5
6
23
23
3
25
36
22
×
=
33
32
×
×
=
3 .计算
(1)(-2)3×(-2)5
(2) (-2)2×(-2)7
(3) (-2)3×25
(4) (-2)2×27
(5)(x)2(-x)3(-x)
(6)32×3×9 - 3×34
=28
=-29
=-28
=29
=x6
=0
已知:am=2,an=3.求am+n =?
拓展延伸
解: am+n =
am · an
=2 × 3
=6
(2)已知:an-3×a2n+1=a10,则n=_______
(3)如果2n=2,2m=8,则3n×3m =____.
4
81
(1)已知x =2,x =3,求x _______
a
b
a+b
6
能力提高
小结感悟
1. 对自己说,你有什么收获?
2. 对同学说,你有什么温馨提示?
3. 对老师说,你还有什么困惑?
布置作业,强化目标
作业:习题1.1
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
