湘教版数学八年级上册同步课件:2.1 第2课时 三角形的高、角平分线和中线(共15张PPT)
文档属性
| 名称 | 湘教版数学八年级上册同步课件:2.1 第2课时 三角形的高、角平分线和中线(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 220.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 10:37:15 | ||
图片预览





文档简介
(共15张PPT)
第二章 三角形
2.1 第2课时 三角形的高、角平分线和中线
知识回顾
请大家回忆,小学学过三角形的哪些重要线段?你对它有何认识?
说一说
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫作三角形的高线(altitude), 简称三角形的高. 如图2-6, AH⊥BC, 垂足为点H, 则线段AH是△ABC的BC边上的高.
A
B
C
图2-6
H
高线
获取新知
如图2-7, 试画出图中△ABC的BC 边上的高.
A
B
C
图2-7
做一做
除了高,
初中我们再介绍两种三角形的重要线段.
在三角形中,一个角的平分线与这个角的对边相交, 这个角的顶点与交点之间的线段叫作三角形的角平分线. 如图2-8, ∠BAD=∠CAD, 则线段AD是△ABC的一条角平分线.
A
B
C
图2-8
D
角平分线
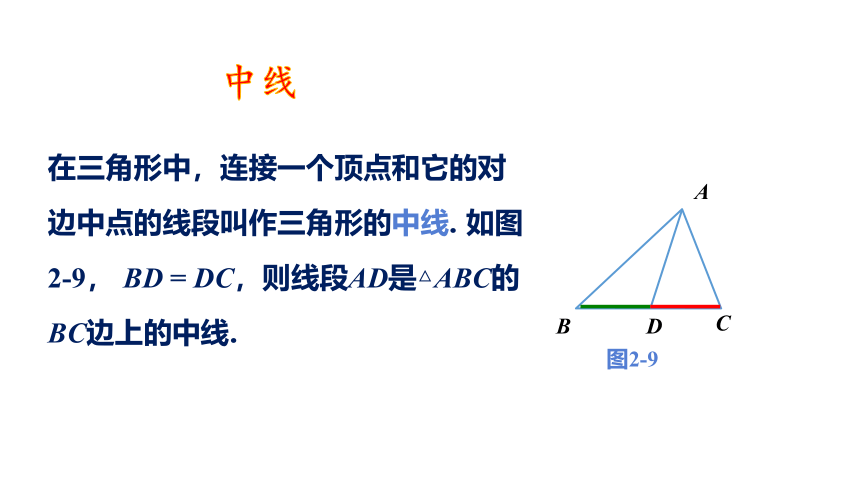
在三角形中,连接一个顶点和它的对边中点的线段叫作三角形的中线. 如图2-9, BD = DC,则线段AD是△ABC的BC边上的中线.
A
B
C
图2-9
D
中线
任意画一个三角形, 画出三边上的中线. 你发现了什么?
做一做
事实上, 三角形的三条中线相交于一点. 我们把这三条中线的交点叫作三角形的重心. 如图2-10, △ABC 的三条中线AD, BE, CF 相交于点G, 则点G 为△ABC 的重心.
A
B
C
图2-10
D
E
F
G
重心
(1)一个三角形中三条中线(高、角平分线)之间的位置关系怎样
(2)一个三角形的三条中线(角平分线)的交点与三角形有怎样的位置关系
(3)直角三角形的三条高,它们有怎样的位置关系 钝角三角形呢
三条中线交于一点,三条角平分线交于一点,三条高所在的直线交于一点
三条中线(角平分线)相交于一点,这一点在三角形内部
直角三角形有一条高在三角形内部,另外两条就是直角三角形的两条直角边,三条高的交点就是直角三角形的直角顶点,钝角三角形有一条高在形内,两条高在形外,三条高所在的直线的交点在形外。
例2 如图2-11, AD是△ABC的中线, AE是△ABC的高.
(1) 图中共有几个三角形? 请分别列举出来.
(2) 其中哪些三角形的面积相等?
A
B
C
D
E
图2-11
解(1) 图中有6个三角形, 它们分别是:
△ABD, △ADE, △AEC,
△ABE, △ADC, △ABC.
例题讲解
(2) 因为AD是△ABC的中线,
所以BD = DC.
因为AE是△ABC的高,也是△ABD和 △ADC的高,
又
所以
A
B
C
D
E
图2-11
通过反思本题第二问,你有什么发现?
三角形中线把三角形平分成面积相等的两部分.
1. 利用三角尺(或直尺)、量角器任意画出一个三角形, 并画出其中一条边上的中线、高以及这条边所对的角的平分线.
随堂演练
2. 如图, AD是△ABC 的高, DE 是△ADB 的中线, BF 是△EBD 的角平分线, 根据已知条件填空:
(1) ∠ADB =∠ = °;
(2) BE = = ;
(3) ∠DBF =∠ = ∠ .
A
B
C
D
E
F
ADC
90
AE
AB
EBF
EBD
3.三角形的下列线段中能将三角形的面积分成相等两部分的是( )
A.中线 B.角平分线 C.高 D.中位线
解析
根据中线的定义,“连接三角形一个顶点和它对边中点的线段叫做三角形的中线”,知三角形的中线把三角形分成等底同高的两个三角形,它们的面积相等.
A
课堂小结
1.从知识上,在小学学习的基础上,我们又学习了什么?
2.从方法上,我们是怎么认识这些重要线段的,对你后续的学习有什么启示吗?
第二章 三角形
2.1 第2课时 三角形的高、角平分线和中线
知识回顾
请大家回忆,小学学过三角形的哪些重要线段?你对它有何认识?
说一说
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫作三角形的高线(altitude), 简称三角形的高. 如图2-6, AH⊥BC, 垂足为点H, 则线段AH是△ABC的BC边上的高.
A
B
C
图2-6
H
高线
获取新知
如图2-7, 试画出图中△ABC的BC 边上的高.
A
B
C
图2-7
做一做
除了高,
初中我们再介绍两种三角形的重要线段.
在三角形中,一个角的平分线与这个角的对边相交, 这个角的顶点与交点之间的线段叫作三角形的角平分线. 如图2-8, ∠BAD=∠CAD, 则线段AD是△ABC的一条角平分线.
A
B
C
图2-8
D
角平分线
在三角形中,连接一个顶点和它的对边中点的线段叫作三角形的中线. 如图2-9, BD = DC,则线段AD是△ABC的BC边上的中线.
A
B
C
图2-9
D
中线
任意画一个三角形, 画出三边上的中线. 你发现了什么?
做一做
事实上, 三角形的三条中线相交于一点. 我们把这三条中线的交点叫作三角形的重心. 如图2-10, △ABC 的三条中线AD, BE, CF 相交于点G, 则点G 为△ABC 的重心.
A
B
C
图2-10
D
E
F
G
重心
(1)一个三角形中三条中线(高、角平分线)之间的位置关系怎样
(2)一个三角形的三条中线(角平分线)的交点与三角形有怎样的位置关系
(3)直角三角形的三条高,它们有怎样的位置关系 钝角三角形呢
三条中线交于一点,三条角平分线交于一点,三条高所在的直线交于一点
三条中线(角平分线)相交于一点,这一点在三角形内部
直角三角形有一条高在三角形内部,另外两条就是直角三角形的两条直角边,三条高的交点就是直角三角形的直角顶点,钝角三角形有一条高在形内,两条高在形外,三条高所在的直线的交点在形外。
例2 如图2-11, AD是△ABC的中线, AE是△ABC的高.
(1) 图中共有几个三角形? 请分别列举出来.
(2) 其中哪些三角形的面积相等?
A
B
C
D
E
图2-11
解(1) 图中有6个三角形, 它们分别是:
△ABD, △ADE, △AEC,
△ABE, △ADC, △ABC.
例题讲解
(2) 因为AD是△ABC的中线,
所以BD = DC.
因为AE是△ABC的高,也是△ABD和 △ADC的高,
又
所以
A
B
C
D
E
图2-11
通过反思本题第二问,你有什么发现?
三角形中线把三角形平分成面积相等的两部分.
1. 利用三角尺(或直尺)、量角器任意画出一个三角形, 并画出其中一条边上的中线、高以及这条边所对的角的平分线.
随堂演练
2. 如图, AD是△ABC 的高, DE 是△ADB 的中线, BF 是△EBD 的角平分线, 根据已知条件填空:
(1) ∠ADB =∠ = °;
(2) BE = = ;
(3) ∠DBF =∠ = ∠ .
A
B
C
D
E
F
ADC
90
AE
AB
EBF
EBD
3.三角形的下列线段中能将三角形的面积分成相等两部分的是( )
A.中线 B.角平分线 C.高 D.中位线
解析
根据中线的定义,“连接三角形一个顶点和它对边中点的线段叫做三角形的中线”,知三角形的中线把三角形分成等底同高的两个三角形,它们的面积相等.
A
课堂小结
1.从知识上,在小学学习的基础上,我们又学习了什么?
2.从方法上,我们是怎么认识这些重要线段的,对你后续的学习有什么启示吗?
同课章节目录
