湘教版数学八年级上册同步课件:2.1.3三角形内角和定理(共19张PPT)
文档属性
| 名称 | 湘教版数学八年级上册同步课件:2.1.3三角形内角和定理(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 427.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 10:59:41 | ||
图片预览





文档简介
(共19张PPT)
第二章 三角形
2.1 第3课时 三角形内角和定理
知识回顾
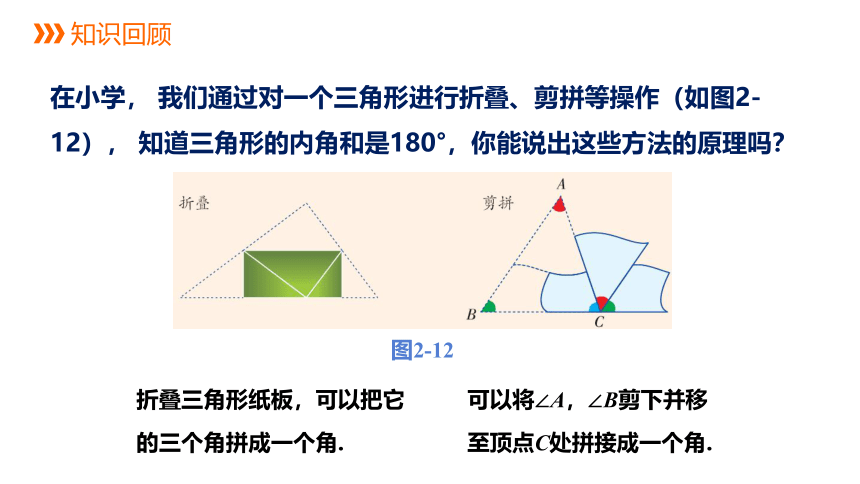
在小学, 我们通过对一个三角形进行折叠、剪拼等操作(如图2-12), 知道三角形的内角和是180°,你能说出这些方法的原理吗?
折叠三角形纸板,可以把它
的三个角拼成一个角.
可以将∠A,∠B剪下并移
至顶点C处拼接成一个角.
图2-12
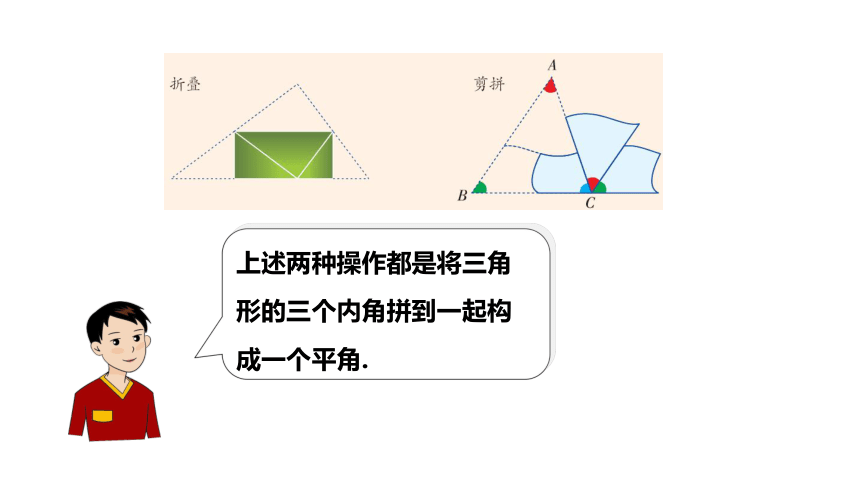
上述两种操作都是将三角形的三个内角拼到一起构成一个平角.
因为直线在平移下的像是与它平行的直线,
所以B′C′∥BC.
则∠B′AB =∠B,∠C′AC =∠C.
又∠B′AB +∠BAC +∠C′AC = 180°,
所以∠B +∠BAC +∠C = 180°.
由此受到启发:
如图2-13, 将△ABC的边BC 所在的直线平移,使其像经过点A, 得到直线B′C′.
A
B
C
图2-13
B′
C′
获取新知
结论
三角形的内角和等于180°.
三角形内角和定理还有没有别的证法呢?
多种方法证明的核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角.
例题讲解
例3 在△ABC 中, ∠A 的度数是∠B 的度数的3倍,∠C 比∠B 大15°,求∠A,∠B,∠C的度数.
解 设∠B为x°,则∠A为(3x )°,∠C为(x + 15) °, 从而有
3x + x +( x + 15 )= 180.
解得 x = 33.
所以 3x = 99 , x + 15 = 48.
答: ∠A, ∠B, ∠C的度数分别为99°, 33°, 48°.
三角形按角如何分类呢?
探究
获取新知
一个三角形的三个内角中, 最多有几个直角? 最多有几个钝角?
三角形的内角和等于180°,
因此最多有一个直角或一个钝角.
说一说
三角形中, 三个角都是锐角的三角形叫锐角三角形, 有一个角是直角的三角形叫直角三角形, 有一个角是钝角的三角形叫钝角三角形, 如图2-14.
图2-14
锐角三角形 直角三角形 钝角三角形
直角三角形可用符号“Rt△” 来表示,
例如直角三角形ABC 可以记作“Rt△ABC”.
在直角三角形中, 夹直角的两边叫作直角边, 直角的对边叫作斜边.
两条直角边相等的直角三角形叫作等腰直角三角形.
如图2-15, 把△ABC的一边BC延长, 得到∠ACD. 像这样, 三角形的一边与另一边的延长线所组成的角, 叫作三角形的外角.
对外角∠ACD来说, ∠ACB是与它相邻的内角, ∠A, ∠B是与它不相邻的内角.
B
C
图2-15
A
D
探究
在图2-15 中, 外角∠ACD 和与它不相邻的内角∠A, ∠B 之间有什么大小关系?
我觉得可以利用“三角形的内角和等于180° ” 的结论.
因为∠ACD +∠ACB = 180°,
∠A +∠B +∠ACB = 180°,
所以∠ACD -∠A -∠B = 0
(等量减等量, 差相等).
于是∠ACD =∠A +∠B.
B
C
图2-15
A
D
结论
三角形的一个外角等于与它不相邻的两个内角的和.
1. 填空:
(1) 在△ABC中, ∠A= 60°, ∠B=∠C, 则∠B= ;
(2) 在△ABC中, ∠A-∠B= 50°, ∠C-∠B= 40°, 则∠B= .
60°
30°
随堂演练
2. 如图, AD是△ABC的角平分线, ∠B= 36°, ∠C= 76°, 求∠DAC的度数.
A
B
C
D
36°
76°
解 因为∠B= 36°, ∠C= 76°
又 ∠BAC+∠B+∠C=180°,
因为 AD是△ABC的角平分线,
所以 ∠BAC=68°,
所以
3. 如图,∠CAD=100°,∠B= 30°,求∠C的度数.
A
B
C
D
30°
100°
解 因为∠CAD是△ABC的外角,
于是∠C = ∠CAD -∠B
= 100°-30°=70°
所以 ∠B+∠C= ∠CAD ,
4.如图,在△ABC中,∠B=47°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=______°
解析
∵∠B=47°,
∴ ∠BAC+∠BCA=180°– 47°=133°,∴∠CAD+∠ACF=360°–133°=227°,
又 AE和CE是角平分线,∴∠CAE+∠ACE=113.5°,∴∠E=180°–113.5°=66.5.
66.5
A
B
C
F
E
D
1.这节课我们研究的是什么?为什么要这么研究?
2.从方法上你有哪些收获?
3.“一题多解,多解归一”,需要把多种解法的共性挖掘出来,归纳成解决一类问题的方法.
课堂小结
第二章 三角形
2.1 第3课时 三角形内角和定理
知识回顾
在小学, 我们通过对一个三角形进行折叠、剪拼等操作(如图2-12), 知道三角形的内角和是180°,你能说出这些方法的原理吗?
折叠三角形纸板,可以把它
的三个角拼成一个角.
可以将∠A,∠B剪下并移
至顶点C处拼接成一个角.
图2-12
上述两种操作都是将三角形的三个内角拼到一起构成一个平角.
因为直线在平移下的像是与它平行的直线,
所以B′C′∥BC.
则∠B′AB =∠B,∠C′AC =∠C.
又∠B′AB +∠BAC +∠C′AC = 180°,
所以∠B +∠BAC +∠C = 180°.
由此受到启发:
如图2-13, 将△ABC的边BC 所在的直线平移,使其像经过点A, 得到直线B′C′.
A
B
C
图2-13
B′
C′
获取新知
结论
三角形的内角和等于180°.
三角形内角和定理还有没有别的证法呢?
多种方法证明的核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角.
例题讲解
例3 在△ABC 中, ∠A 的度数是∠B 的度数的3倍,∠C 比∠B 大15°,求∠A,∠B,∠C的度数.
解 设∠B为x°,则∠A为(3x )°,∠C为(x + 15) °, 从而有
3x + x +( x + 15 )= 180.
解得 x = 33.
所以 3x = 99 , x + 15 = 48.
答: ∠A, ∠B, ∠C的度数分别为99°, 33°, 48°.
三角形按角如何分类呢?
探究
获取新知
一个三角形的三个内角中, 最多有几个直角? 最多有几个钝角?
三角形的内角和等于180°,
因此最多有一个直角或一个钝角.
说一说
三角形中, 三个角都是锐角的三角形叫锐角三角形, 有一个角是直角的三角形叫直角三角形, 有一个角是钝角的三角形叫钝角三角形, 如图2-14.
图2-14
锐角三角形 直角三角形 钝角三角形
直角三角形可用符号“Rt△” 来表示,
例如直角三角形ABC 可以记作“Rt△ABC”.
在直角三角形中, 夹直角的两边叫作直角边, 直角的对边叫作斜边.
两条直角边相等的直角三角形叫作等腰直角三角形.
如图2-15, 把△ABC的一边BC延长, 得到∠ACD. 像这样, 三角形的一边与另一边的延长线所组成的角, 叫作三角形的外角.
对外角∠ACD来说, ∠ACB是与它相邻的内角, ∠A, ∠B是与它不相邻的内角.
B
C
图2-15
A
D
探究
在图2-15 中, 外角∠ACD 和与它不相邻的内角∠A, ∠B 之间有什么大小关系?
我觉得可以利用“三角形的内角和等于180° ” 的结论.
因为∠ACD +∠ACB = 180°,
∠A +∠B +∠ACB = 180°,
所以∠ACD -∠A -∠B = 0
(等量减等量, 差相等).
于是∠ACD =∠A +∠B.
B
C
图2-15
A
D
结论
三角形的一个外角等于与它不相邻的两个内角的和.
1. 填空:
(1) 在△ABC中, ∠A= 60°, ∠B=∠C, 则∠B= ;
(2) 在△ABC中, ∠A-∠B= 50°, ∠C-∠B= 40°, 则∠B= .
60°
30°
随堂演练
2. 如图, AD是△ABC的角平分线, ∠B= 36°, ∠C= 76°, 求∠DAC的度数.
A
B
C
D
36°
76°
解 因为∠B= 36°, ∠C= 76°
又 ∠BAC+∠B+∠C=180°,
因为 AD是△ABC的角平分线,
所以 ∠BAC=68°,
所以
3. 如图,∠CAD=100°,∠B= 30°,求∠C的度数.
A
B
C
D
30°
100°
解 因为∠CAD是△ABC的外角,
于是∠C = ∠CAD -∠B
= 100°-30°=70°
所以 ∠B+∠C= ∠CAD ,
4.如图,在△ABC中,∠B=47°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=______°
解析
∵∠B=47°,
∴ ∠BAC+∠BCA=180°– 47°=133°,∴∠CAD+∠ACF=360°–133°=227°,
又 AE和CE是角平分线,∴∠CAE+∠ACE=113.5°,∴∠E=180°–113.5°=66.5.
66.5
A
B
C
F
E
D
1.这节课我们研究的是什么?为什么要这么研究?
2.从方法上你有哪些收获?
3.“一题多解,多解归一”,需要把多种解法的共性挖掘出来,归纳成解决一类问题的方法.
课堂小结
同课章节目录
