湘教版数学八年级上册同步课件:2.3.1 等腰(边)三角形的性质(共22张PPT)
文档属性
| 名称 | 湘教版数学八年级上册同步课件:2.3.1 等腰(边)三角形的性质(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 328.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 00:00:00 | ||
图片预览


文档简介
(共22张PPT)
第二章 三角形
2.3 第1课时 等腰(边)三角形的性质
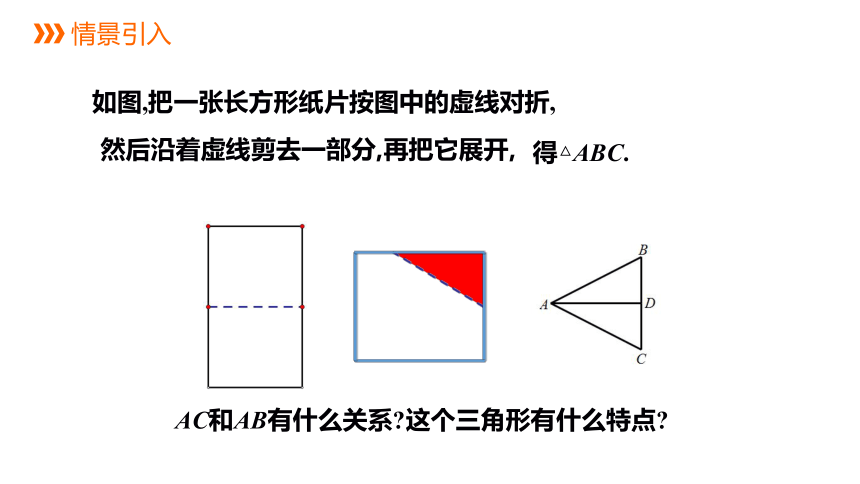
情景引入
如图,把一张长方形纸片按图中的虚线对折,
AC和AB有什么关系 这个三角形有什么特点
然后沿着虚线剪去一部分,再把它展开,
得△ABC.
一.基本概念
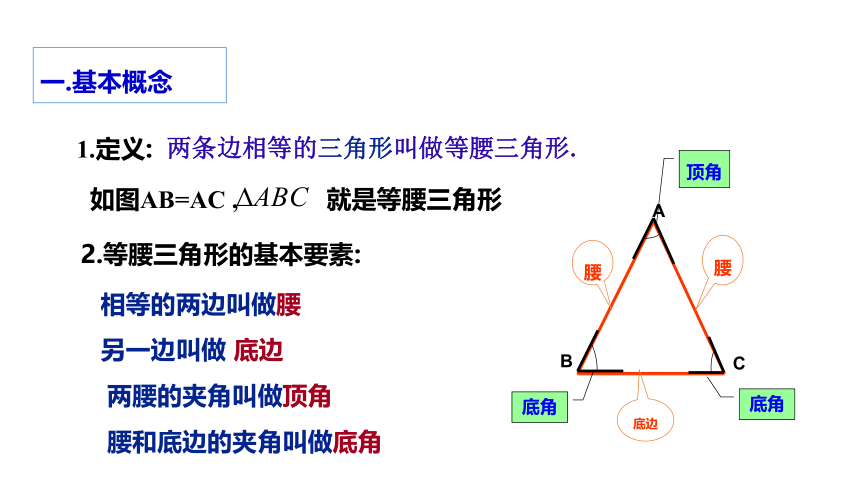
1.定义:
两条边相等的三角形叫做等腰三角形.
如图AB=AC , 就是等腰三角形
2.等腰三角形的基本要素:
相等的两边叫做腰
另一边叫做 底边
两腰的夹角叫做顶角
腰和底边的夹角叫做底角
A
B
C
腰
腰
底边
顶角
底角
底角
C
A
B
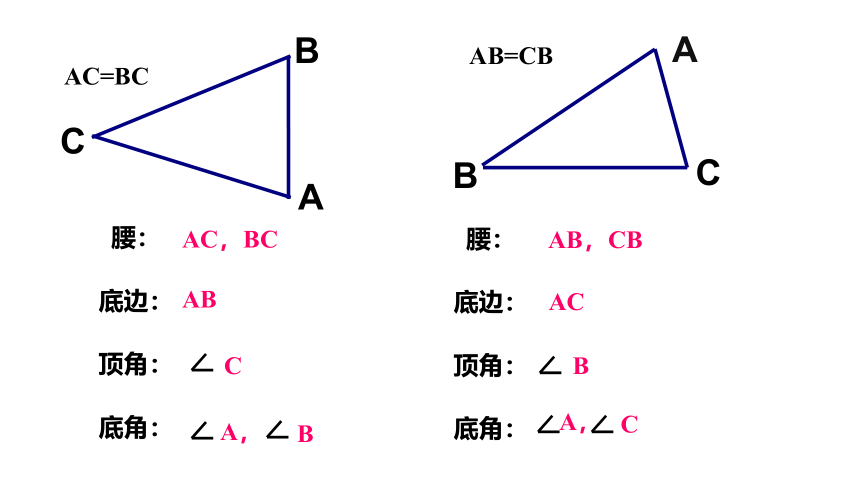
AC=BC
B
C
A
AB=CB
腰:
底边:
顶角:
底角:
腰:
底边:
顶角:
底角:
AC,BC
AB
A,
B
AB,CB
AC
B
A,
C
C
探究
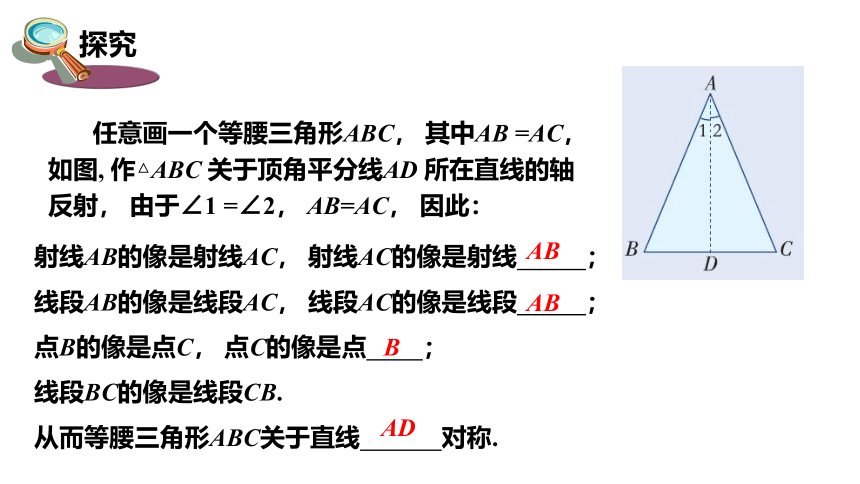
任意画一个等腰三角形ABC, 其中AB =AC, 如图, 作△ABC 关于顶角平分线AD 所在直线的轴反射, 由于∠1 =∠2, AB=AC, 因此:
射线AB的像是射线AC, 射线AC的像是射线 ;
线段AB的像是线段AC, 线段AC的像是线段 ;
点B的像是点C, 点C的像是点 ;
线段BC的像是线段CB.
从而等腰三角形ABC关于直线 对称.
AB
AB
B
AD
获取新知
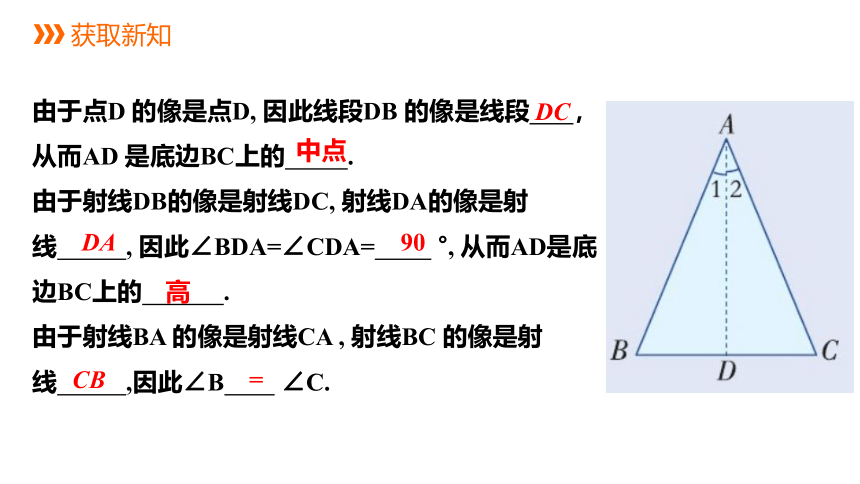
由于点D 的像是点D, 因此线段DB 的像是线段 , 从而AD 是底边BC上的 .
由于射线DB的像是射线DC, 射线DA的像是射线 , 因此∠BDA=∠CDA= °, 从而AD是底边BC上的 .
由于射线BA 的像是射线CA , 射线BC 的像是射线 ,因此∠B ∠C.
DC
中点
DA
90
高
CB
=
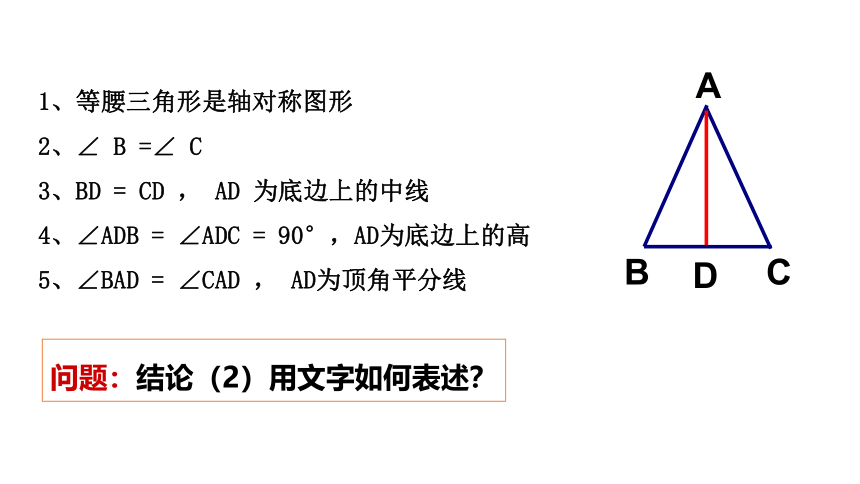
1、等腰三角形是轴对称图形
2、∠ B =∠ C
3、BD = CD , AD 为底边上的中线
4、∠ADB = ∠ADC = 90°,AD为底边上的高
5、∠BAD = ∠CAD , AD为顶角平分线
问题:结论(2)用文字如何表述?
C
A
B
D
结论
等腰三角形是轴对称图形,
对称轴是顶角平分线所在的直线.
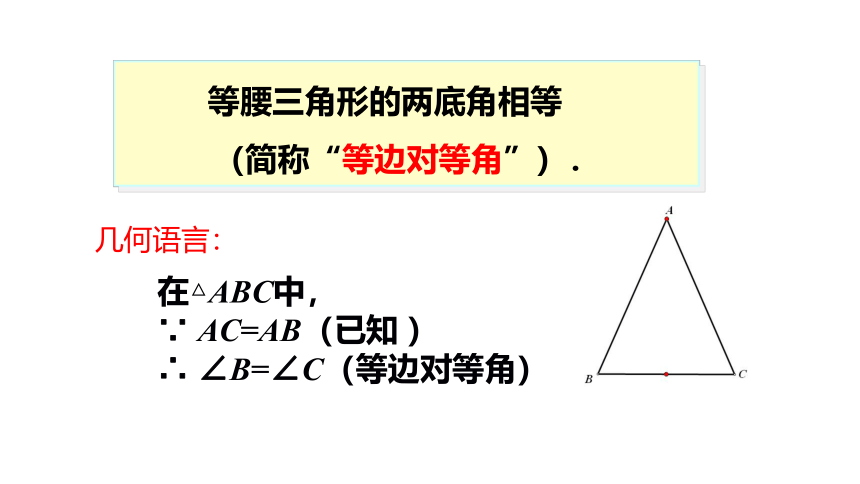
等腰三角形的两底角相等
(简称“等边对等角”).
在△ABC中,
∵ AC=AB(已知 )
∴ ∠B=∠C(等边对等角)
几何语言:
等腰三角形底边上的高、中线及顶角平分线重合
(简称“三线合一”).
在△ABC中,AB =AC, 点 D在BC上
1、∵AD ⊥ BC
∴∠ = ∠ , = .
2、∵AD是中线,
∴ ⊥ ,∠ =∠ .
3、∵AD是角平分线,
∴ ⊥ , = .
几何语言:
BAD CAD
BD CD
BD CD
BAD CAD
AD BC
AD BC
在△ABC中,AB=AC,点D在AC上,BD=BC=AD,求△ ABC各角的度数 .
解:∵在△ABC中,AB=AC
∴∠ABC=∠ACB,∠A+∠ABC+∠ACB=180°
∵在△ABD中,BD=AD
∴∠ABD=∠A,∠BDC=∠A+∠ABD,
即∠BDC=2∠A
∵ 在△BDC中,BD=BC
∴∠BDC=∠BCD,
∠A+2∠ACB=180°
即 ∠A+4∠A=180°
∴∠A=36°
∠ABC=∠BCA=2∠A=72°
如图(1)在等腰△ABC中,
AB =AC, ∠A = 36°,则∠B = ,∠C= .
变式练习:
1、如图(2)在等腰△ABC中,∠A = 50°, 则∠B = ,∠C= .
2、如图(3)在等腰△ABC中,∠A = 120°则∠B = ,∠C= .
72 °
72 °
65 °
65 °
30 °
30 °
想一想
如图, △ABC 是等边三角形, 那么∠A, ∠B,∠C的大小之间有什么关系呢?
因为△ABC 是等边三角形,
所以AB=BC=AC,
从而∠C =∠A=∠B
由三角形内角和定理可得:
∠A=∠B=∠C = 60°.
等边三角形的三个内角相等,且都等于60°.
由于等边三角形是特殊的等腰三角形,因此等边三角形是轴对称图形,它有三条对称轴,分别是三个内角的平分线所在的直线.
例1
已知: 如图, 在△ABC中, AB=AC, BD⊥AC, 垂足为点D.
求证: ∠DBC= ∠A.
作AF⊥BC于F
∵AB=AC AF⊥BC
∴∠CAF=∠BAF= ∠BAC
∵AF⊥BC BD⊥AC
∴∠CAF+∠C=∠DBC+∠C=90°
∴∠DBC =∠CAF
∴∠DBC= ∠BAC
解
解题规律:在等腰三角形中,做顶角平分线或作底边上高或作底边上中线是一种常用的辅助线.
例题讲解
已知: 如图, 在△ABC 中, AB = AC,点D, E在边BC上, 且AD = AE.
求证: BD = CE.
证明:作AF⊥BC,垂足为点F, 则AF 是等腰三角形ABC 和等腰三角形ADE 底边上的高, 也是底边上的中线.
∴ BF = CF,
DF = EF,
∴ BF - DF = CF - EF,
即BD = CE.
例2
如图 的三角测平架中,AB=AC,在BC的中点D 挂一个重锤,自然下垂,调整架身, 使点A恰好在铅垂线上.
AD与BC是否垂直,试说明理由;
(2) 这时BC处于水平位置,为什么
议一议
垂直,三线合一
AD为铅垂线,BC垂直于AD,所以处于水平位置
1. 如图,在△ABC中,AB=AC,AD为BC边上的高,∠BAC=49°,BC= 4,求∠BAD的度数及DC的长.
答:∠BAD=24.5°
DC=2.
随堂演练
2. 如图,点P为等边三角形ABC的边BC上一点,且∠APD= 80°,AD=AP,求∠DPC的度数.
答:∠DPC =20°.
3.等腰三角形两边长分别是2cm和5cm,则这个三角形周长为( )
A.9cm B.12cm
C.9cm或12cm D.14cm
B
解析
另一边长为2cm或5cm,2,2,5不符合三角形三边关系定理,故选5.
∴周长为5+5+2=12cm.
4. 若等腰三角形中有一个角等于50°,则这个等腰三角形的顶角的度数为( )
A. 50° B. 80°
C. 65°或50° D. 50°或80°
解析
因为50°可作为等腰三角形的一顶角或一底角,故选D.
D
本节课你学习了等腰三角形的哪些重要性质
1、等腰三角形的性质:
等边对等角
2、等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合
3、等边三角形的性质。
等边三角形的三个内角相等,且都等于60°.
(三线合一)
课堂小结
第二章 三角形
2.3 第1课时 等腰(边)三角形的性质
情景引入
如图,把一张长方形纸片按图中的虚线对折,
AC和AB有什么关系 这个三角形有什么特点
然后沿着虚线剪去一部分,再把它展开,
得△ABC.
一.基本概念
1.定义:
两条边相等的三角形叫做等腰三角形.
如图AB=AC , 就是等腰三角形
2.等腰三角形的基本要素:
相等的两边叫做腰
另一边叫做 底边
两腰的夹角叫做顶角
腰和底边的夹角叫做底角
A
B
C
腰
腰
底边
顶角
底角
底角
C
A
B
AC=BC
B
C
A
AB=CB
腰:
底边:
顶角:
底角:
腰:
底边:
顶角:
底角:
AC,BC
AB
A,
B
AB,CB
AC
B
A,
C
C
探究
任意画一个等腰三角形ABC, 其中AB =AC, 如图, 作△ABC 关于顶角平分线AD 所在直线的轴反射, 由于∠1 =∠2, AB=AC, 因此:
射线AB的像是射线AC, 射线AC的像是射线 ;
线段AB的像是线段AC, 线段AC的像是线段 ;
点B的像是点C, 点C的像是点 ;
线段BC的像是线段CB.
从而等腰三角形ABC关于直线 对称.
AB
AB
B
AD
获取新知
由于点D 的像是点D, 因此线段DB 的像是线段 , 从而AD 是底边BC上的 .
由于射线DB的像是射线DC, 射线DA的像是射线 , 因此∠BDA=∠CDA= °, 从而AD是底边BC上的 .
由于射线BA 的像是射线CA , 射线BC 的像是射线 ,因此∠B ∠C.
DC
中点
DA
90
高
CB
=
1、等腰三角形是轴对称图形
2、∠ B =∠ C
3、BD = CD , AD 为底边上的中线
4、∠ADB = ∠ADC = 90°,AD为底边上的高
5、∠BAD = ∠CAD , AD为顶角平分线
问题:结论(2)用文字如何表述?
C
A
B
D
结论
等腰三角形是轴对称图形,
对称轴是顶角平分线所在的直线.
等腰三角形的两底角相等
(简称“等边对等角”).
在△ABC中,
∵ AC=AB(已知 )
∴ ∠B=∠C(等边对等角)
几何语言:
等腰三角形底边上的高、中线及顶角平分线重合
(简称“三线合一”).
在△ABC中,AB =AC, 点 D在BC上
1、∵AD ⊥ BC
∴∠ = ∠ , = .
2、∵AD是中线,
∴ ⊥ ,∠ =∠ .
3、∵AD是角平分线,
∴ ⊥ , = .
几何语言:
BAD CAD
BD CD
BD CD
BAD CAD
AD BC
AD BC
在△ABC中,AB=AC,点D在AC上,BD=BC=AD,求△ ABC各角的度数 .
解:∵在△ABC中,AB=AC
∴∠ABC=∠ACB,∠A+∠ABC+∠ACB=180°
∵在△ABD中,BD=AD
∴∠ABD=∠A,∠BDC=∠A+∠ABD,
即∠BDC=2∠A
∵ 在△BDC中,BD=BC
∴∠BDC=∠BCD,
∠A+2∠ACB=180°
即 ∠A+4∠A=180°
∴∠A=36°
∠ABC=∠BCA=2∠A=72°
如图(1)在等腰△ABC中,
AB =AC, ∠A = 36°,则∠B = ,∠C= .
变式练习:
1、如图(2)在等腰△ABC中,∠A = 50°, 则∠B = ,∠C= .
2、如图(3)在等腰△ABC中,∠A = 120°则∠B = ,∠C= .
72 °
72 °
65 °
65 °
30 °
30 °
想一想
如图, △ABC 是等边三角形, 那么∠A, ∠B,∠C的大小之间有什么关系呢?
因为△ABC 是等边三角形,
所以AB=BC=AC,
从而∠C =∠A=∠B
由三角形内角和定理可得:
∠A=∠B=∠C = 60°.
等边三角形的三个内角相等,且都等于60°.
由于等边三角形是特殊的等腰三角形,因此等边三角形是轴对称图形,它有三条对称轴,分别是三个内角的平分线所在的直线.
例1
已知: 如图, 在△ABC中, AB=AC, BD⊥AC, 垂足为点D.
求证: ∠DBC= ∠A.
作AF⊥BC于F
∵AB=AC AF⊥BC
∴∠CAF=∠BAF= ∠BAC
∵AF⊥BC BD⊥AC
∴∠CAF+∠C=∠DBC+∠C=90°
∴∠DBC =∠CAF
∴∠DBC= ∠BAC
解
解题规律:在等腰三角形中,做顶角平分线或作底边上高或作底边上中线是一种常用的辅助线.
例题讲解
已知: 如图, 在△ABC 中, AB = AC,点D, E在边BC上, 且AD = AE.
求证: BD = CE.
证明:作AF⊥BC,垂足为点F, 则AF 是等腰三角形ABC 和等腰三角形ADE 底边上的高, 也是底边上的中线.
∴ BF = CF,
DF = EF,
∴ BF - DF = CF - EF,
即BD = CE.
例2
如图 的三角测平架中,AB=AC,在BC的中点D 挂一个重锤,自然下垂,调整架身, 使点A恰好在铅垂线上.
AD与BC是否垂直,试说明理由;
(2) 这时BC处于水平位置,为什么
议一议
垂直,三线合一
AD为铅垂线,BC垂直于AD,所以处于水平位置
1. 如图,在△ABC中,AB=AC,AD为BC边上的高,∠BAC=49°,BC= 4,求∠BAD的度数及DC的长.
答:∠BAD=24.5°
DC=2.
随堂演练
2. 如图,点P为等边三角形ABC的边BC上一点,且∠APD= 80°,AD=AP,求∠DPC的度数.
答:∠DPC =20°.
3.等腰三角形两边长分别是2cm和5cm,则这个三角形周长为( )
A.9cm B.12cm
C.9cm或12cm D.14cm
B
解析
另一边长为2cm或5cm,2,2,5不符合三角形三边关系定理,故选5.
∴周长为5+5+2=12cm.
4. 若等腰三角形中有一个角等于50°,则这个等腰三角形的顶角的度数为( )
A. 50° B. 80°
C. 65°或50° D. 50°或80°
解析
因为50°可作为等腰三角形的一顶角或一底角,故选D.
D
本节课你学习了等腰三角形的哪些重要性质
1、等腰三角形的性质:
等边对等角
2、等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合
3、等边三角形的性质。
等边三角形的三个内角相等,且都等于60°.
(三线合一)
课堂小结
同课章节目录
