湘教版数学八年级上册同步课件:2.3.2等腰(边)三角形的判定(共18张PPT)
文档属性
| 名称 | 湘教版数学八年级上册同步课件:2.3.2等腰(边)三角形的判定(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 428.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 11:07:44 | ||
图片预览




文档简介
(共18张PPT)
第二章 三角形
2.3 第2课时 等腰(边)三角形的判定
知识回顾
1、等腰三角形是怎样定义的?
有两条边相等的三角形,叫做等腰三角形。
③等腰三角形是轴对称图形。
②等腰三角形顶角的平分线、底边上的中线、底边上的高重合。 (简称“三线合一”).
①等腰三角形的两个底角相等。 (简写成“等边对等角”)
2、等腰三角形有哪些性质?
D
A
B
C
把“等腰三角形的两个底角相等”改写成“如果------那么-----”的形式。
如果一个三角形有两个角相等,那么这个三角形是等腰三角形.
如果一个三角形是等腰三角形,那么这个三角形的两个底角相等.
求上述命题的逆命题,并判断真假。
我们知道,等腰三角形的两底角相等,反过来,两个角相等的三角形是等腰三角形吗?
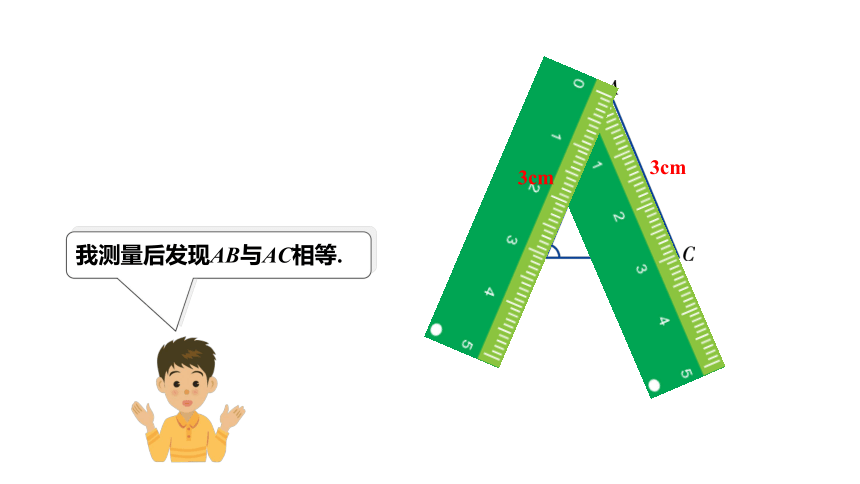
如图,在△ABC中,如果∠B=∠C,那么AB与AC之间有什么关系吗?
情景引入
我测量后发现AB与AC相等.
3cm
3cm
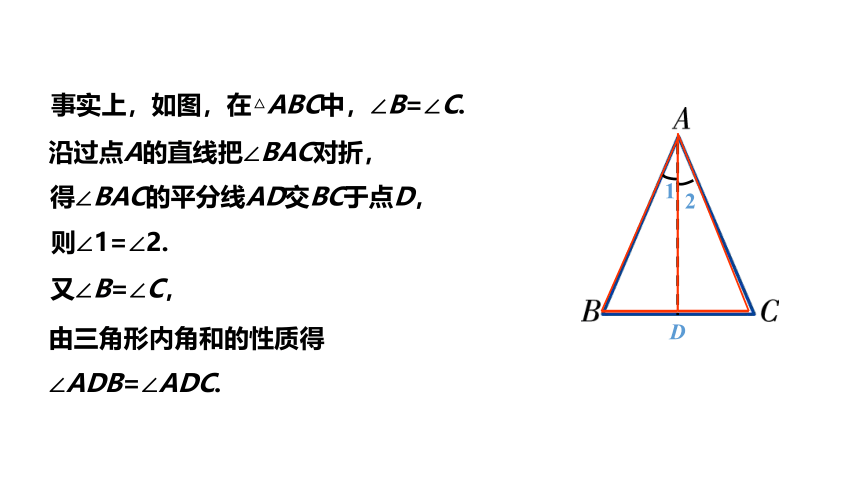
事实上,如图,在△ABC中,∠B=∠C.
沿过点A的直线把∠BAC对折,
得∠BAC的平分线AD交BC于点D,
则∠1=∠2.
又∠B=∠C,
由三角形内角和的性质得
∠ADB=∠ADC.
D
1
2
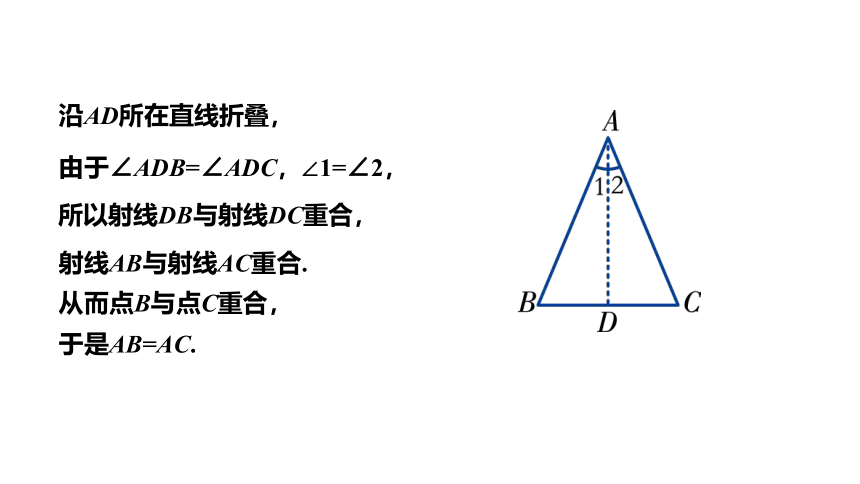
沿AD所在直线折叠,
由于∠ADB=∠ADC,∠1=∠2,
所以射线DB与射线DC重合,
射线AB与射线AC重合.
从而点B与点C重合,
于是AB=AC.
有两个角相等的三角形是等腰三角形
(简称“等角对等边”).
获取新知
三个角都是60°的三角形是等边三角形.
由此并且结合三角形内角和定理,还可以得到等边三角形的判定定理:
A
B
C
例2 已知:如图,在△ABC中,AB=AC,点D,E分别是AB,AC上的点,且DE∥BC.
求证:△ADE为等腰三角形.
证明 ∵AB=AC,
∴ ∠B=∠C.
又∵ DE∥BC,
∴ ∠ADE=∠B,∠AED=∠C.
∴ ∠ADE=∠AED.
于是△ADE为等腰三角形.
例题讲解
有一个角是60°的等腰三角形是等边三角形吗?为什么?
动脑筋
如图,在等腰三角形ABC中,
AB=AC.
由三角形内角和定理得
∠A+∠B+∠C= 180°.
如果顶角∠A=60°,
则∠B+∠C= 180°-60°=120°.
又 AB=AC,
∴ ∠B=∠C.
∴ ∠B=∠C=∠A=60°.
∴ △ABC是等边三角形.
如果底角∠B=60°或∠C=60°呢?
由此得到另一条等边三角形的判定定理:
结论
有一个角是60°的等腰三角形是等边三角形
例3 已知:如图,△ABC是等边三角形,点D,E分别在BA,CA的延长线上,且AD=AE.
求证:△ADE是等边三角形.
证明 ∵△ABC是等边三角形,
∴∠BAC=∠B=∠C= 60°.
∵∠EAD=∠BAC= 60°,
又 AD =AE,
∴△ADE是等边三角形
(有一个角是60°的等腰三角形是等边三角形)
例题讲解
1. 已知:等腰三角形ABC的底角∠ABC和∠ACB的平分线相交于点O.
求证:△OBC为等腰三角形.
A
B
C
D
E
O
证明
∵∠ABC 和∠ACB的平分线相交于点O,
∴ ∠ABD =∠DBC= ,
∠ACE =∠ECB= ,
∴ ∠DBC =∠ECB,
∴ △OBC是等腰三角形.
又∵ △ABC是等腰三角形,
∴ ∠ABC =∠ACB,
随堂演练
2. 已知:如图,CD平分∠ACB,AE∥DC,AE交BC的延长线于点E,且∠ACE= 60°.
求证:△ACE是等边三角形.
证明
∵CD平分∠ACB,
∴ 在△ACE中,∠CAE= 180°- ∠E -∠ACE =60 °
又∵∠ACE=60°,
∴ ∠BCD=∠E=60°,
∴ ∠ACD =∠DCB,
∴ ∠ACD=∠DCB=60°,
又 ∵ AE∥DC,
∴ ∠CAE = ∠ACE=∠E=60°
∴△ACE是等边三角形.
3. 已知:如图,AB=BC ,∠CDE= 120°, DF∥BA,且DF平分∠CDE.
求证:△ABC是等边三角形.
证明
∵ AB=BC,
∴△ABC是等边三角形.
又∵∠CDE=120°,DF平分∠CDE.
∴ ∠FDC=∠ABC=60°,
∴ △ABC是等腰三角形,
∴ ∠EDF=∠FDC=60°,
又∵DF∥BA,
课堂小结
第二章 三角形
2.3 第2课时 等腰(边)三角形的判定
知识回顾
1、等腰三角形是怎样定义的?
有两条边相等的三角形,叫做等腰三角形。
③等腰三角形是轴对称图形。
②等腰三角形顶角的平分线、底边上的中线、底边上的高重合。 (简称“三线合一”).
①等腰三角形的两个底角相等。 (简写成“等边对等角”)
2、等腰三角形有哪些性质?
D
A
B
C
把“等腰三角形的两个底角相等”改写成“如果------那么-----”的形式。
如果一个三角形有两个角相等,那么这个三角形是等腰三角形.
如果一个三角形是等腰三角形,那么这个三角形的两个底角相等.
求上述命题的逆命题,并判断真假。
我们知道,等腰三角形的两底角相等,反过来,两个角相等的三角形是等腰三角形吗?
如图,在△ABC中,如果∠B=∠C,那么AB与AC之间有什么关系吗?
情景引入
我测量后发现AB与AC相等.
3cm
3cm
事实上,如图,在△ABC中,∠B=∠C.
沿过点A的直线把∠BAC对折,
得∠BAC的平分线AD交BC于点D,
则∠1=∠2.
又∠B=∠C,
由三角形内角和的性质得
∠ADB=∠ADC.
D
1
2
沿AD所在直线折叠,
由于∠ADB=∠ADC,∠1=∠2,
所以射线DB与射线DC重合,
射线AB与射线AC重合.
从而点B与点C重合,
于是AB=AC.
有两个角相等的三角形是等腰三角形
(简称“等角对等边”).
获取新知
三个角都是60°的三角形是等边三角形.
由此并且结合三角形内角和定理,还可以得到等边三角形的判定定理:
A
B
C
例2 已知:如图,在△ABC中,AB=AC,点D,E分别是AB,AC上的点,且DE∥BC.
求证:△ADE为等腰三角形.
证明 ∵AB=AC,
∴ ∠B=∠C.
又∵ DE∥BC,
∴ ∠ADE=∠B,∠AED=∠C.
∴ ∠ADE=∠AED.
于是△ADE为等腰三角形.
例题讲解
有一个角是60°的等腰三角形是等边三角形吗?为什么?
动脑筋
如图,在等腰三角形ABC中,
AB=AC.
由三角形内角和定理得
∠A+∠B+∠C= 180°.
如果顶角∠A=60°,
则∠B+∠C= 180°-60°=120°.
又 AB=AC,
∴ ∠B=∠C.
∴ ∠B=∠C=∠A=60°.
∴ △ABC是等边三角形.
如果底角∠B=60°或∠C=60°呢?
由此得到另一条等边三角形的判定定理:
结论
有一个角是60°的等腰三角形是等边三角形
例3 已知:如图,△ABC是等边三角形,点D,E分别在BA,CA的延长线上,且AD=AE.
求证:△ADE是等边三角形.
证明 ∵△ABC是等边三角形,
∴∠BAC=∠B=∠C= 60°.
∵∠EAD=∠BAC= 60°,
又 AD =AE,
∴△ADE是等边三角形
(有一个角是60°的等腰三角形是等边三角形)
例题讲解
1. 已知:等腰三角形ABC的底角∠ABC和∠ACB的平分线相交于点O.
求证:△OBC为等腰三角形.
A
B
C
D
E
O
证明
∵∠ABC 和∠ACB的平分线相交于点O,
∴ ∠ABD =∠DBC= ,
∠ACE =∠ECB= ,
∴ ∠DBC =∠ECB,
∴ △OBC是等腰三角形.
又∵ △ABC是等腰三角形,
∴ ∠ABC =∠ACB,
随堂演练
2. 已知:如图,CD平分∠ACB,AE∥DC,AE交BC的延长线于点E,且∠ACE= 60°.
求证:△ACE是等边三角形.
证明
∵CD平分∠ACB,
∴ 在△ACE中,∠CAE= 180°- ∠E -∠ACE =60 °
又∵∠ACE=60°,
∴ ∠BCD=∠E=60°,
∴ ∠ACD =∠DCB,
∴ ∠ACD=∠DCB=60°,
又 ∵ AE∥DC,
∴ ∠CAE = ∠ACE=∠E=60°
∴△ACE是等边三角形.
3. 已知:如图,AB=BC ,∠CDE= 120°, DF∥BA,且DF平分∠CDE.
求证:△ABC是等边三角形.
证明
∵ AB=BC,
∴△ABC是等边三角形.
又∵∠CDE=120°,DF平分∠CDE.
∴ ∠FDC=∠ABC=60°,
∴ △ABC是等腰三角形,
∴ ∠EDF=∠FDC=60°,
又∵DF∥BA,
课堂小结
同课章节目录
