湘教版数学八年级上册同步课件:2.5 第1课时 全等三角形的概念和性质(共19张PPT)
文档属性
| 名称 | 湘教版数学八年级上册同步课件:2.5 第1课时 全等三角形的概念和性质(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 512.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 23:07:02 | ||
图片预览




文档简介
(共19张PPT)
第二章 三角形
2.5 第1课时 全等三角形的概念和性质
情景引入
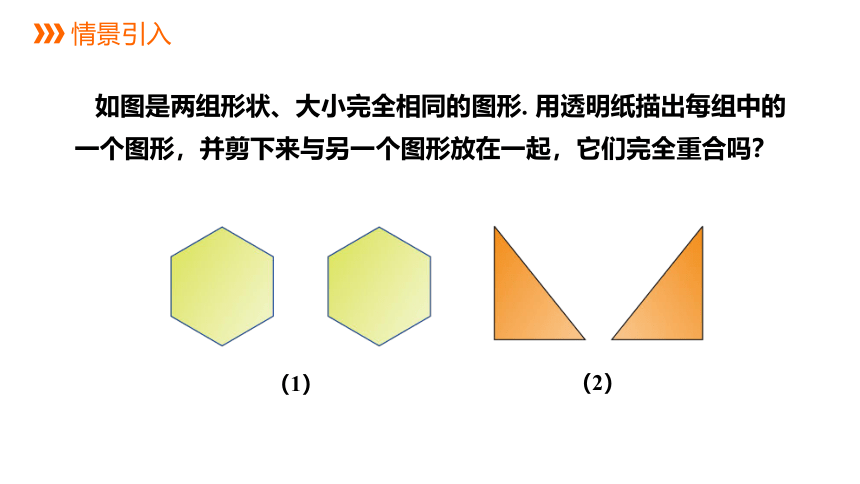
如图是两组形状、大小完全相同的图形. 用透明纸描出每组中的一个图形,并剪下来与另一个图形放在一起,它们完全重合吗?
(1)
(2)
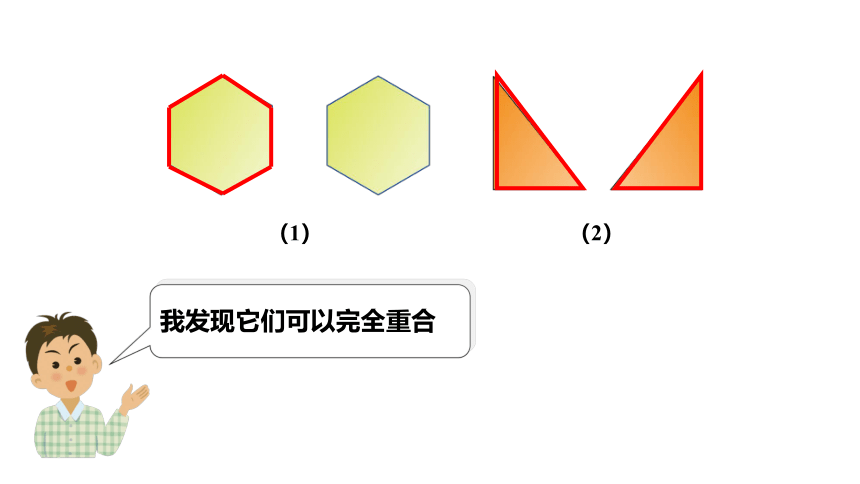
(1)
(2)
我发现它们可以完全重合
结论
我们把能够完全重合的两个图形叫作全等图形.
获取新知
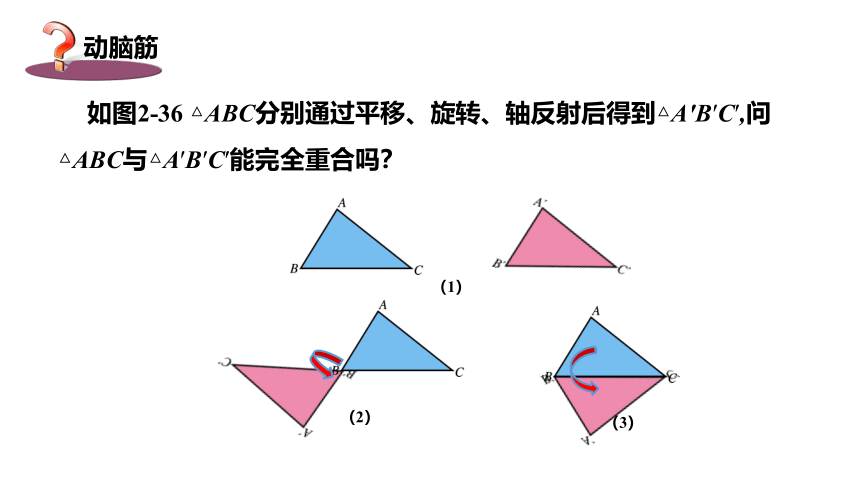
(1)
(2)
(3)
如图2-36 △ABC分别通过平移、旋转、轴反射后得到△A′B′C′,问△ABC与△A′B′C′能完全重合吗?
动脑筋
根据平移、旋转和轴反射的性质,可知分别通过上述三个变换后得到的△ 与△ABC都可以完全重合,因此它们是全等图形.
结论
能完全重合的两个三角形叫作全等三角形.
获取新知
全等三角形中,互相重合的顶点叫作对应顶点,
互相重合的边叫作对应边,
互相重合的角叫作对应角.
A′
B′
C′
A
B
C
A(A′)
B(B′)
C(C′)
例如,图(1)中的△ABC和△ 全等,
其中A与A′,B与B′,C与C′是对应顶点;
记作: △ABC ≌ △ .
AB与 ,BC与 ,CA与 是对应边;
∠A与∠A′,∠B与∠B′,∠C与∠C′是对应角.
(1)
小提示
全等用符号“≌”表示,读作“全等于”
在表示两个三角形全等时,通常把表示对应顶点的字母写在对应位置上.
结论
全等三角形的对应边相等;
全等三角形的对应角相等.
我们知道,能够完全重合的两条线段是相等的,能够完全重合的两个角是相等的,由此得到:
例如,
(1)
例1 如图,已知△ABC≌△DCB,AB=3,DB=4,∠A=60°.
(1)写出△ABC和△DCB的对应边和对应角;
(2)求AC,DC的长及∠D的度数.
解(1)AB与DC,AC与DB,
BC与CB是对应边;
∠A与∠D,∠ABC与∠DCB,
∠ACB与∠DBC是对应角.
例题讲解
∴ AC = DB = 4,
DC = AB =3.
(2)∵ AC与DB,
AB与DC是全等三角形的对应边,
∵∠A与∠D是全等三角形的对应角,
∴∠D =∠A = 60°.
解:其他对应边:AN与AM,BN与CM.
其他对应角:∠BAN与∠CAM,∠ANB与∠AMC.
1. 如图,已知△ADF≌△CBE,AD=4,BE=3,AF=6,∠A=20°,∠B=120°.
(1)找出它们的所有对应边和对应角;
(2)求△ADF的周长及∠BEC的度数.
解(1)AF与CE,AD与CB,
DF与BE是对应边;
∠A与∠C,∠AFD与∠CEB,
∠D与∠B是对应角.
(2)△ADF的周长是13,∠BEC=40°.
随堂演练
30
∠DBE
CA
20
2.全等三角形的定义是什么?
1.全等图形的定义是什么?
能够完全重合的两个图形叫作全等图形.
能完全重合的两个三角形叫作全等三角形.
3.全等三角形的性质是什么?
全等三角形的对应边相等;
全等三角形的对应角相等.
课堂小结
第二章 三角形
2.5 第1课时 全等三角形的概念和性质
情景引入
如图是两组形状、大小完全相同的图形. 用透明纸描出每组中的一个图形,并剪下来与另一个图形放在一起,它们完全重合吗?
(1)
(2)
(1)
(2)
我发现它们可以完全重合
结论
我们把能够完全重合的两个图形叫作全等图形.
获取新知
(1)
(2)
(3)
如图2-36 △ABC分别通过平移、旋转、轴反射后得到△A′B′C′,问△ABC与△A′B′C′能完全重合吗?
动脑筋
根据平移、旋转和轴反射的性质,可知分别通过上述三个变换后得到的△ 与△ABC都可以完全重合,因此它们是全等图形.
结论
能完全重合的两个三角形叫作全等三角形.
获取新知
全等三角形中,互相重合的顶点叫作对应顶点,
互相重合的边叫作对应边,
互相重合的角叫作对应角.
A′
B′
C′
A
B
C
A(A′)
B(B′)
C(C′)
例如,图(1)中的△ABC和△ 全等,
其中A与A′,B与B′,C与C′是对应顶点;
记作: △ABC ≌ △ .
AB与 ,BC与 ,CA与 是对应边;
∠A与∠A′,∠B与∠B′,∠C与∠C′是对应角.
(1)
小提示
全等用符号“≌”表示,读作“全等于”
在表示两个三角形全等时,通常把表示对应顶点的字母写在对应位置上.
结论
全等三角形的对应边相等;
全等三角形的对应角相等.
我们知道,能够完全重合的两条线段是相等的,能够完全重合的两个角是相等的,由此得到:
例如,
(1)
例1 如图,已知△ABC≌△DCB,AB=3,DB=4,∠A=60°.
(1)写出△ABC和△DCB的对应边和对应角;
(2)求AC,DC的长及∠D的度数.
解(1)AB与DC,AC与DB,
BC与CB是对应边;
∠A与∠D,∠ABC与∠DCB,
∠ACB与∠DBC是对应角.
例题讲解
∴ AC = DB = 4,
DC = AB =3.
(2)∵ AC与DB,
AB与DC是全等三角形的对应边,
∵∠A与∠D是全等三角形的对应角,
∴∠D =∠A = 60°.
解:其他对应边:AN与AM,BN与CM.
其他对应角:∠BAN与∠CAM,∠ANB与∠AMC.
1. 如图,已知△ADF≌△CBE,AD=4,BE=3,AF=6,∠A=20°,∠B=120°.
(1)找出它们的所有对应边和对应角;
(2)求△ADF的周长及∠BEC的度数.
解(1)AF与CE,AD与CB,
DF与BE是对应边;
∠A与∠C,∠AFD与∠CEB,
∠D与∠B是对应角.
(2)△ADF的周长是13,∠BEC=40°.
随堂演练
30
∠DBE
CA
20
2.全等三角形的定义是什么?
1.全等图形的定义是什么?
能够完全重合的两个图形叫作全等图形.
能完全重合的两个三角形叫作全等三角形.
3.全等三角形的性质是什么?
全等三角形的对应边相等;
全等三角形的对应角相等.
课堂小结
同课章节目录
