湘教版数学八年级上册同步课件:2.5 第3课时 全等三角形的判定2——“ASA”(共14张PPT)
文档属性
| 名称 | 湘教版数学八年级上册同步课件:2.5 第3课时 全等三角形的判定2——“ASA”(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 261.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
第二章 三角形
2.5 第3课时 全等三角形的判定2——“ASA”
知识回顾
什么叫全等三角形?
两个能完全重合的三角形叫做全等三角形。
全等三角形的对应边、对应角有什么重要性质?
全等三角形的对应边相等,对应角相等。
如何判断两个三角形是全等三角形
两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”
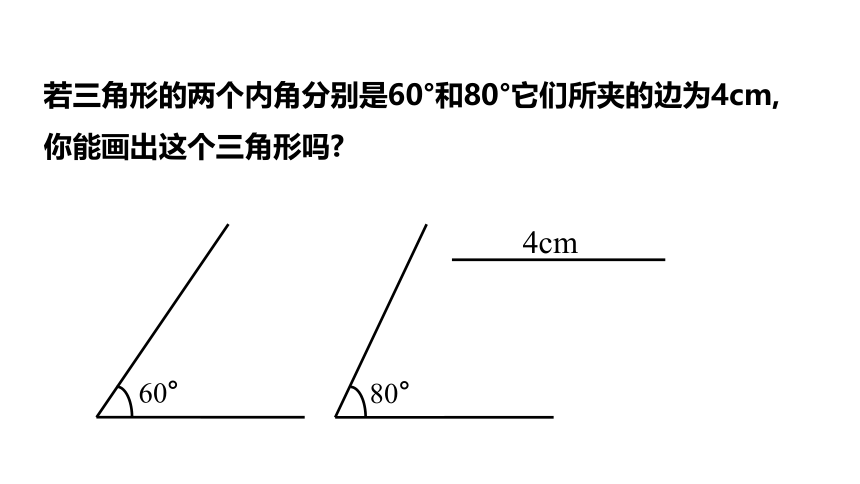
若三角形的两个内角分别是60°和80°它们所夹的边为4cm,你能画出这个三角形吗
4cm
60°
80°
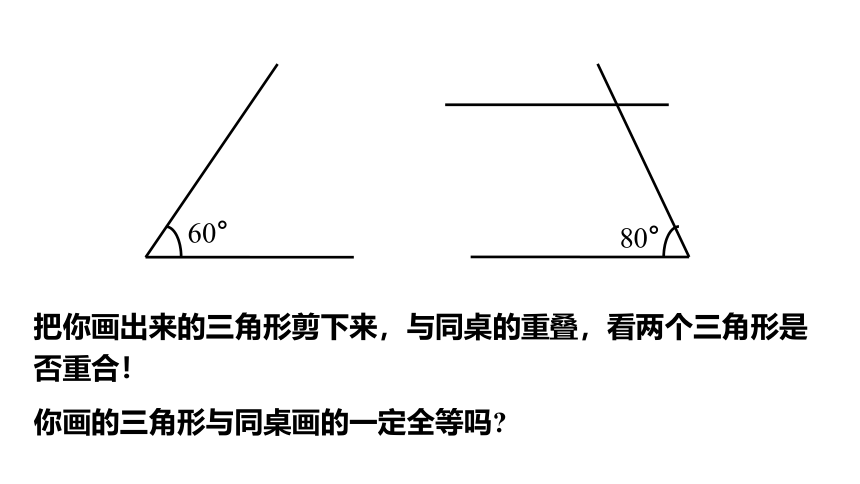
把你画出来的三角形剪下来,与同桌的重叠,看两个三角形是否重合!
60°
80°
你画的三角形与同桌画的一定全等吗
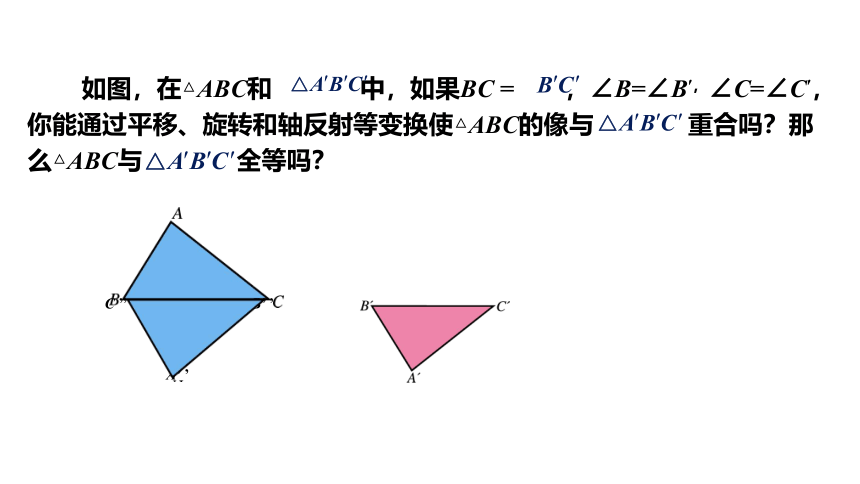
如图,在△ABC和 中,如果BC = ,∠B=∠B′,∠C=∠C′,你能通过平移、旋转和轴反射等变换使△ABC的像与 重合吗?那么△ABC与 全等吗?
B’ ’
C ’’
A’ ’
获取新知
类似于基本事实“SAS”的探究,同样地,我们可以通过平移、旋转和轴反射等变换使△ABC的像与 重合,因此
△ABC ≌
例题讲解
由此得到判定两个三角形全等的基本事实:
两角及其夹边分别相等的两个三角形全等.
通常可简写成“角边角”或“ASA”.
例3 已知:如图,点A,F,E,C在同一条直线上,AB∥DC,AB=CD,∠B=∠D.
求证:△ABE≌△CDF.
证明 ∵ AB∥DC,
∴ ∠A=∠C.
在△ABE和△CDF中,
∴ △ABE≌△CDF (ASA).
∠A=∠C,
AB = CD,
∠B=∠D,
获取新知
例4 如图,为测量河宽AB,小军从河岸的A点沿着和AB垂直的方向走到C点,并在AC的中点E处立一根标杆,然后从C点沿着与AC垂直的方向走到D点,使D,E,B恰好在一条直线上. 于是小军说:“CD的长就是河的宽.”你能说出这个道理吗?
A
B
E
C
D
解:
在△AEB和△CED中,
∠A =∠C = 90°,
AE = CE,
∠AEB =∠CED (对顶角相等)
∴ △AEB ≌ △CED.(ASA)
∴ AB=CD .(全等三角形的对应边相等)
因此,CD的长就是河的宽度.
1. 如图,工人师傅不小心把一块三角形玻璃打碎成三块,现要到玻璃店重新配一块与原来一样的三角形玻璃,只允许带其中的一块玻璃碎片
去. 请问应带哪块玻璃碎片去?为什么?
答:应带玻璃碎片③去;只有这块玻璃具备决定全等三角形的几个条件:在三角形中已知两个角和它们所夹的边,由ASA判定定理即可确定两个三角形全等,故应带这块玻璃去.
随堂演练
2. 已知:如图,△ABC≌ ,CF, 分别是∠ACB和 的平分线.
求证:
△ABC≌△A′B′C′,
∠A =∠A′ ,
∠ACB =∠A′C′B′.
∴
AC=A′C′
证明:
∴ CF=C′F′.
又CF,C′F′分别是∠ACB和∠A′C′B′的平分线,
∴ ∠ACF=∠A′C′F′.
∴ △ACF≌△A′C′F′
ACE
∠ACF=∠DBE
或FC∥EB
课堂小结
1.这两节课学习哪些判定两个三角形全等的方法?
2.这两个判定方法是如何得到的?
3.判定两个三角形全等可以帮助我们解决哪些问题?
证明线段(或角相等) 证明线段(或角)所在的两个三角形全等.
转化
SAS、ASA
平移、旋转和轴反射等变换
4.书写证明过程时需注意什么?
(1) 证明两个三角形全等所需的条件应按对应边、对应角、对应边顺序书写;
(2)“边角边”中的“角”必须是两边的夹角;
(3)“角边角”中的“边”必须是两角的夹边.
第二章 三角形
2.5 第3课时 全等三角形的判定2——“ASA”
知识回顾
什么叫全等三角形?
两个能完全重合的三角形叫做全等三角形。
全等三角形的对应边、对应角有什么重要性质?
全等三角形的对应边相等,对应角相等。
如何判断两个三角形是全等三角形
两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”
若三角形的两个内角分别是60°和80°它们所夹的边为4cm,你能画出这个三角形吗
4cm
60°
80°
把你画出来的三角形剪下来,与同桌的重叠,看两个三角形是否重合!
60°
80°
你画的三角形与同桌画的一定全等吗
如图,在△ABC和 中,如果BC = ,∠B=∠B′,∠C=∠C′,你能通过平移、旋转和轴反射等变换使△ABC的像与 重合吗?那么△ABC与 全等吗?
B’ ’
C ’’
A’ ’
获取新知
类似于基本事实“SAS”的探究,同样地,我们可以通过平移、旋转和轴反射等变换使△ABC的像与 重合,因此
△ABC ≌
例题讲解
由此得到判定两个三角形全等的基本事实:
两角及其夹边分别相等的两个三角形全等.
通常可简写成“角边角”或“ASA”.
例3 已知:如图,点A,F,E,C在同一条直线上,AB∥DC,AB=CD,∠B=∠D.
求证:△ABE≌△CDF.
证明 ∵ AB∥DC,
∴ ∠A=∠C.
在△ABE和△CDF中,
∴ △ABE≌△CDF (ASA).
∠A=∠C,
AB = CD,
∠B=∠D,
获取新知
例4 如图,为测量河宽AB,小军从河岸的A点沿着和AB垂直的方向走到C点,并在AC的中点E处立一根标杆,然后从C点沿着与AC垂直的方向走到D点,使D,E,B恰好在一条直线上. 于是小军说:“CD的长就是河的宽.”你能说出这个道理吗?
A
B
E
C
D
解:
在△AEB和△CED中,
∠A =∠C = 90°,
AE = CE,
∠AEB =∠CED (对顶角相等)
∴ △AEB ≌ △CED.(ASA)
∴ AB=CD .(全等三角形的对应边相等)
因此,CD的长就是河的宽度.
1. 如图,工人师傅不小心把一块三角形玻璃打碎成三块,现要到玻璃店重新配一块与原来一样的三角形玻璃,只允许带其中的一块玻璃碎片
去. 请问应带哪块玻璃碎片去?为什么?
答:应带玻璃碎片③去;只有这块玻璃具备决定全等三角形的几个条件:在三角形中已知两个角和它们所夹的边,由ASA判定定理即可确定两个三角形全等,故应带这块玻璃去.
随堂演练
2. 已知:如图,△ABC≌ ,CF, 分别是∠ACB和 的平分线.
求证:
△ABC≌△A′B′C′,
∠A =∠A′ ,
∠ACB =∠A′C′B′.
∴
AC=A′C′
证明:
∴ CF=C′F′.
又CF,C′F′分别是∠ACB和∠A′C′B′的平分线,
∴ ∠ACF=∠A′C′F′.
∴ △ACF≌△A′C′F′
ACE
∠ACF=∠DBE
或FC∥EB
课堂小结
1.这两节课学习哪些判定两个三角形全等的方法?
2.这两个判定方法是如何得到的?
3.判定两个三角形全等可以帮助我们解决哪些问题?
证明线段(或角相等) 证明线段(或角)所在的两个三角形全等.
转化
SAS、ASA
平移、旋转和轴反射等变换
4.书写证明过程时需注意什么?
(1) 证明两个三角形全等所需的条件应按对应边、对应角、对应边顺序书写;
(2)“边角边”中的“角”必须是两边的夹角;
(3)“角边角”中的“边”必须是两角的夹边.
同课章节目录
