湘教版八年级上册2.5全等三角形课件(共20张PPT)
文档属性
| 名称 | 湘教版八年级上册2.5全等三角形课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 470.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 14:05:13 | ||
图片预览







文档简介
(共20张PPT)
第二章 三角形
2.5 第2课时 全等三角形的判定1—“SAS”
知识回顾
2.全等三角形的定义是什么?
1.全等图形的定义是什么?
能够完全重合的两个图形叫作全等图形.
能完全重合的两个三角形叫作全等三角形.
3.全等三角形的性质是什么?
全等三角形的对应边相等;
全等三角形的对应角相等.
两个三角形满足什么条件就能全等呢?
下面我们就来探讨这个问题.
情景引入
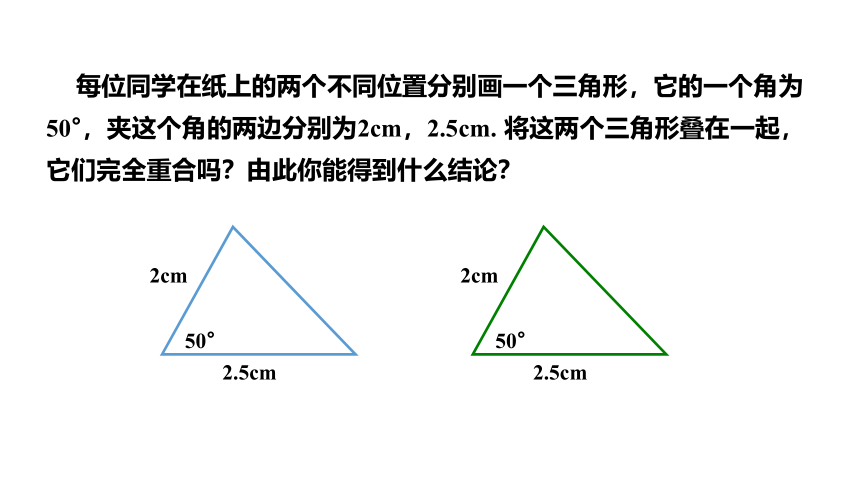
每位同学在纸上的两个不同位置分别画一个三角形,它的一个角为50°,夹这个角的两边分别为2cm,2.5cm. 将这两个三角形叠在一起,它们完全重合吗?由此你能得到什么结论?
50°
2cm
2.5cm
50°
2cm
2.5cm
50°
2cm
2.5cm
我发现它们完全重合,我猜测:有两边和它们的夹角分别相等的两个三角形全等.
下面,我们从以下这几种情形来探讨这个猜测是否为真.
设在△ABC 和 中, ,
1、通过平移
(1)△ABC和 的位置关系如图.
将△ABC作平移,使BC的像 与 重合,△ABC在平移下的像为 .
由于平移不改变图形的形状和大小,因此△ABC≌
1、通过平移
因为 ,
所以线段A″B″与 重合,
因此点 与点 重合,
那么 与 重合,
所以 与 重合,
因此 ,
从而
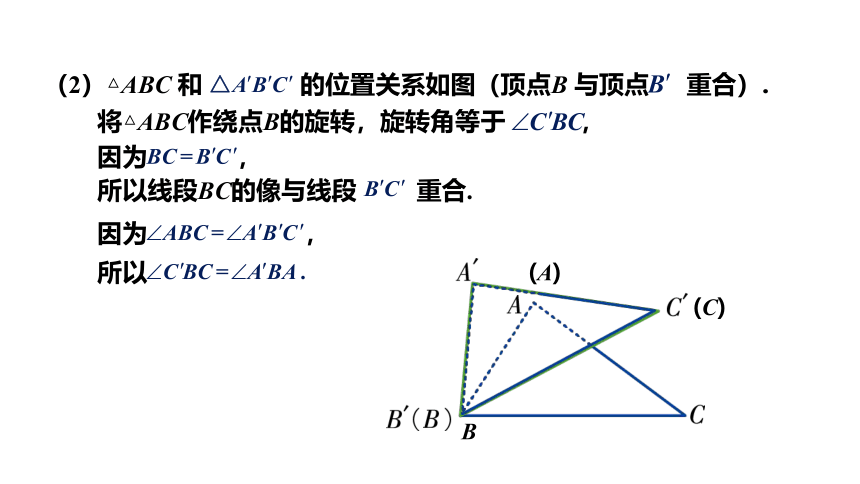
(2)△ABC 和 的位置关系如图(顶点B 与顶点 重合).
因为 ,
将△ABC作绕点B的旋转,旋转角等于 ,
所以线段BC的像与线段 重合.
因为 ,
所以
(A)
B
(C)
由于旋转不改变图形的形状和大小,
又因为 ,
所以在上述旋转下,BA的像与 重合,
从而AC 的像就与 重合,
于是△ABC 的像就是
因此 △ABC ≌
(A)
B
(C)
(3)△ABC和 的位置关系如图.
根据情形(1),(2)的结论得
将△ABC作平移,使顶点B的像 和顶点 重合,
因此
3、通过平移后再旋转
(4)△ABC和 的位置关系如图.
将△ABC作关于直线BC的轴反射,
△ABC在轴反射下的像为
由于轴反射不改变图形的形状和大小,
因此 △ABC ≌
4、通过轴对称变换,然后再平移旋转(结论三)
根据情形(3)的结论得 ,
因此
由此得到判定两个三角形全等的基本事实:
两边及其夹角分别相等的两个三角形全等.
通常可简写成“边角边”或“SAS”.
S ——边 A——角
获取新知
1.在下列图中找出全等三角形,并把它们用符号写出来.
Ⅰ
30
8 cm
9 cm
Ⅵ
30
8 cm
8 cm
Ⅳ
Ⅳ
8 cm
5 cm
Ⅱ
30
8 cm
5 cm
Ⅴ
30
8 cm
5 cm
Ⅷ
8 cm
5 cm
30
8 cm
9 cm
Ⅶ
Ⅲ
30
8 cm
8 cm
Ⅲ
例题讲解
例2 已知:如图,AB和CD相交于O,且AO=BO,CO=DO.
求证:△ACO≌△BDO.
证明:
在△ACO和△BDO中,
∴ △ACO≌△BDO.(SAS)
AO = BO,
∠AOC =∠BOD,(对顶角相等)
CO = DO,
1. 如图,将两根钢条AA′和BB′的中点O连在一起, 使钢条可以绕点O自由转动,就可做成测量工件内槽宽度的工具(卡钳).只要量出 的长,就得出工件内槽的宽AB. 这是根据什么道理呢?
解 △ABO≌△A′B′O,
∴AB= A′B′.
随堂演练
2. 如图,AD∥BC,AD=BC. 问:△ADC和△CBA是全等三角形吗?为什么?
解 ∵ AD∥BC
∴ △ADC≌△CBA.
∴∠DAC=∠BCA,
又 AD=BC,AC公共
3. 已知:如图,AB=AC,点E,F分别是AC,AB的中点.
求证:BE=CF.
解 ∵ AB=AC, 且 E,F分别是AC,AB中点,
∴ △ABE≌△ACF,
∴AF=AE,
又 ∠A公共,
∴ BE=CF.
课堂小结
第二章 三角形
2.5 第2课时 全等三角形的判定1—“SAS”
知识回顾
2.全等三角形的定义是什么?
1.全等图形的定义是什么?
能够完全重合的两个图形叫作全等图形.
能完全重合的两个三角形叫作全等三角形.
3.全等三角形的性质是什么?
全等三角形的对应边相等;
全等三角形的对应角相等.
两个三角形满足什么条件就能全等呢?
下面我们就来探讨这个问题.
情景引入
每位同学在纸上的两个不同位置分别画一个三角形,它的一个角为50°,夹这个角的两边分别为2cm,2.5cm. 将这两个三角形叠在一起,它们完全重合吗?由此你能得到什么结论?
50°
2cm
2.5cm
50°
2cm
2.5cm
50°
2cm
2.5cm
我发现它们完全重合,我猜测:有两边和它们的夹角分别相等的两个三角形全等.
下面,我们从以下这几种情形来探讨这个猜测是否为真.
设在△ABC 和 中, ,
1、通过平移
(1)△ABC和 的位置关系如图.
将△ABC作平移,使BC的像 与 重合,△ABC在平移下的像为 .
由于平移不改变图形的形状和大小,因此△ABC≌
1、通过平移
因为 ,
所以线段A″B″与 重合,
因此点 与点 重合,
那么 与 重合,
所以 与 重合,
因此 ,
从而
(2)△ABC 和 的位置关系如图(顶点B 与顶点 重合).
因为 ,
将△ABC作绕点B的旋转,旋转角等于 ,
所以线段BC的像与线段 重合.
因为 ,
所以
(A)
B
(C)
由于旋转不改变图形的形状和大小,
又因为 ,
所以在上述旋转下,BA的像与 重合,
从而AC 的像就与 重合,
于是△ABC 的像就是
因此 △ABC ≌
(A)
B
(C)
(3)△ABC和 的位置关系如图.
根据情形(1),(2)的结论得
将△ABC作平移,使顶点B的像 和顶点 重合,
因此
3、通过平移后再旋转
(4)△ABC和 的位置关系如图.
将△ABC作关于直线BC的轴反射,
△ABC在轴反射下的像为
由于轴反射不改变图形的形状和大小,
因此 △ABC ≌
4、通过轴对称变换,然后再平移旋转(结论三)
根据情形(3)的结论得 ,
因此
由此得到判定两个三角形全等的基本事实:
两边及其夹角分别相等的两个三角形全等.
通常可简写成“边角边”或“SAS”.
S ——边 A——角
获取新知
1.在下列图中找出全等三角形,并把它们用符号写出来.
Ⅰ
30
8 cm
9 cm
Ⅵ
30
8 cm
8 cm
Ⅳ
Ⅳ
8 cm
5 cm
Ⅱ
30
8 cm
5 cm
Ⅴ
30
8 cm
5 cm
Ⅷ
8 cm
5 cm
30
8 cm
9 cm
Ⅶ
Ⅲ
30
8 cm
8 cm
Ⅲ
例题讲解
例2 已知:如图,AB和CD相交于O,且AO=BO,CO=DO.
求证:△ACO≌△BDO.
证明:
在△ACO和△BDO中,
∴ △ACO≌△BDO.(SAS)
AO = BO,
∠AOC =∠BOD,(对顶角相等)
CO = DO,
1. 如图,将两根钢条AA′和BB′的中点O连在一起, 使钢条可以绕点O自由转动,就可做成测量工件内槽宽度的工具(卡钳).只要量出 的长,就得出工件内槽的宽AB. 这是根据什么道理呢?
解 △ABO≌△A′B′O,
∴AB= A′B′.
随堂演练
2. 如图,AD∥BC,AD=BC. 问:△ADC和△CBA是全等三角形吗?为什么?
解 ∵ AD∥BC
∴ △ADC≌△CBA.
∴∠DAC=∠BCA,
又 AD=BC,AC公共
3. 已知:如图,AB=AC,点E,F分别是AC,AB的中点.
求证:BE=CF.
解 ∵ AB=AC, 且 E,F分别是AC,AB中点,
∴ △ABE≌△ACF,
∴AF=AE,
又 ∠A公共,
∴ BE=CF.
课堂小结
同课章节目录
