湘教版数学八年级上册同步课件 2.5全等三角形性质和判定的应用(第6课时)(共17张PPT)
文档属性
| 名称 | 湘教版数学八年级上册同步课件 2.5全等三角形性质和判定的应用(第6课时)(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 636.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 15:46:09 | ||
图片预览




文档简介
(共17张PPT)
第二章 三角形
2.5 第6课时 全等三角形性质和判定的应用
知识回顾全等三角形的判定方法SSS(边边边)SAS(边角边)ASA(角边角)AAS(角角边)有三边对应相等的两个三角形全等.有两边和它们的夹角对应相等的两个三角形全等.有两角和它们的夹边对应相等的两个三角形全等.有两角和及其中一个角所对的边对应相等的两个三角形全等.
议一议
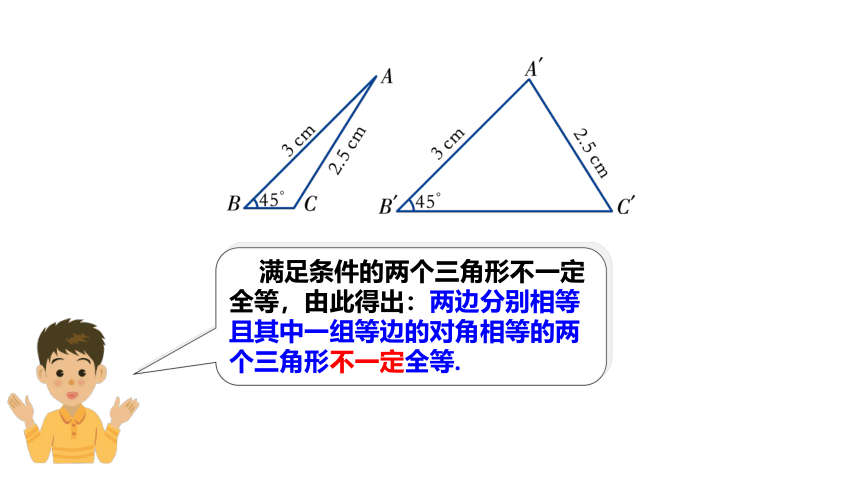
根据下列条件,分别画△ABC和
(1) , , ∠B=∠B′= 45°;
满足上述条件画出的△ABC和 一定全等吗?由此你能得出什么结论?
获取新知
满足条件的两个三角形不一定全等,由此得出:两边分别相等且其中一组等边的对角相等的两个三角形不一定全等.
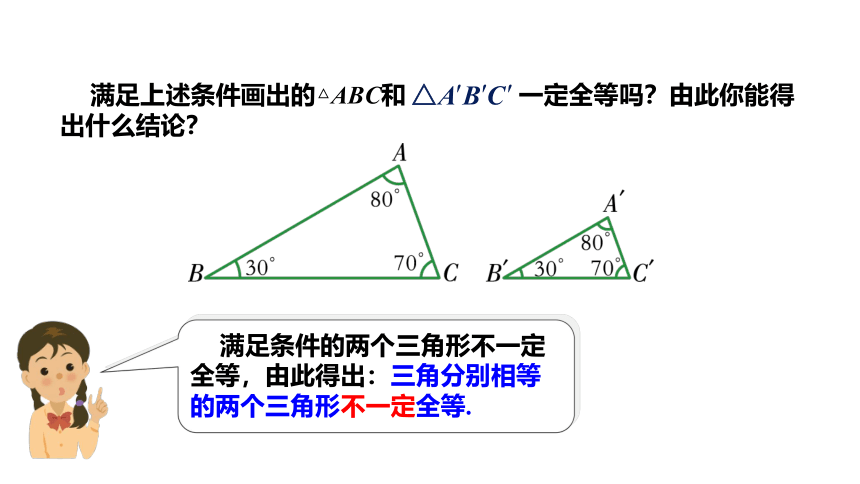
(2) ∠A=∠A′= 80°,∠B=∠B′= 30°, ∠C=∠C′=70°.
满足上述条件画出的△ABC和 一定全等吗?由此你能得出什么结论?
满足条件的两个三角形不一定全等,由此得出:三角分别相等的两个三角形不一定全等.
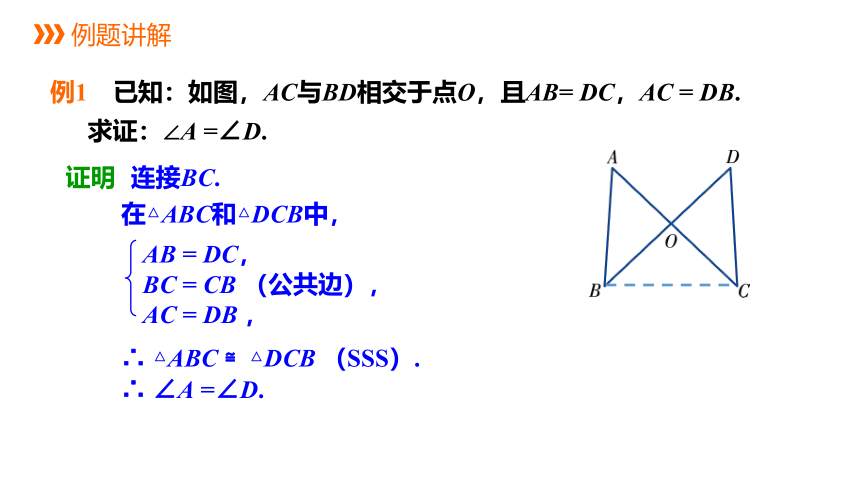
例1 已知:如图,AC与BD相交于点O,且AB= DC,AC = DB.
求证:∠A =∠D.
证明 连接BC.
在△ABC和△DCB中,
∴ △ABC ≌△DCB (SSS).
∴ ∠A =∠D.
AB = DC,
BC = CB (公共边),
AC = DB ,
例题讲解
例2 已知:如图,AB=CD,BC=DA,E,F是AC上的两点,且AE=CE.求证:BF=DE.
D
C
A
B
E
F
证明:在△ABC和△CDA中,
∴ △ABC≌△CDA(SSS).
AB = CD,
BC = DA ,
AC = CA (公共边),
∴ ∠BCF=∠DAE
在△BCF和△DAE中,
∴ △BCF≌△DAE(SAS).
BC = DA ,
∠BCF=∠DAE
CF = AE ,
∴ BF=DE.
例3 某地在山区修建高速公路时需挖通一条隧道. 为估测这条隧道的长度(如图),需测出这座山A,B间的距离,结合所学知识,你能给出什么好方法吗?
解 选择某一合适的地点O,
使得从O点能测出AO与BO的长度.
这样就构造出两个三角形.
连接AO并延长至A′,使 ;
连接BO并延长至B′,使 ,
连接 ,
O
A′
B′
在△AOB和 中,
,
,
,
∴ △AOB≌ (SAS).
∴ AB =
因此只要测出 的长度就能得到这座山A,B间的距离.
1. 已知:如图,AB=AD,BC=DC. 求证:∠B =∠D.
证明 如图,连接AC.
所以 △ACB≌△ ACD (SSS).
所以 ∠B =∠D.
在△ACB和△ACD中,
AB = AD,
BC = CD ,
AC = AC (公共边) ,
随堂演练
2. 如图,在△ABC和△DEC中,已知一些相等的边或角(见下表),请再补充适当的条件,从而能运用已学的判定方法来判定△ABC≌△DEC.
已知条件 补充条件 判定方法
AC=DC,∠A=∠D SAS
∠A=∠D,AB=DE ASA
∠A=∠D,AB=DE AAS
AC=DC,AB=DE SSS
AB=DE
∠B=∠E
∠ACB=∠DCE
BC=EC
3. 如图,在△ABC与△DEF中,已知条件AB=DE,还需添加两个条件才能使△ABC≌△DEF,不能添加的一组条件是( ).
A.∠B=∠E,BC=EF B. BC=EF,AC=DF
C. ∠A=∠D,∠B=∠E D. ∠A=∠D,BC=EF
AB=DE,∠A=∠D,BC=EF 但△ABC与△DEF不全等.
解
D
4. 如图4.2-2,△ACB≌△ ,∠BCB′=30°,则∠ACA′的度数为( ).
A.20° B. 30° C. 35° D. 40°
B
解
∵△ACB≌△ ,
∴ ,
∴ .
故选B.
D
解析:
正确理解运用“SSA”不能判定两个三角形全等:
(1)弄清“SAS”和“SSA”的区别和联系;
(2)不要凭直觉判定两个三角形全等,即使图中所画的两个三角形的确全等,但只要条件是“SSA”,就不能得出全等的结论.
课堂小结
对应相等的元素 两边一角 两角一边 三角 三边
两边及其夹角 两边及其中一边的对角 两角及其夹边 两角及其中一角的对边 三角形是否全等
一定
(SAS)
不一定
一定
(ASA)
一定
(AAS)
不一定
一定
(SSS)
判定三角形全等至少有一组边
第二章 三角形
2.5 第6课时 全等三角形性质和判定的应用
知识回顾全等三角形的判定方法SSS(边边边)SAS(边角边)ASA(角边角)AAS(角角边)有三边对应相等的两个三角形全等.有两边和它们的夹角对应相等的两个三角形全等.有两角和它们的夹边对应相等的两个三角形全等.有两角和及其中一个角所对的边对应相等的两个三角形全等.
议一议
根据下列条件,分别画△ABC和
(1) , , ∠B=∠B′= 45°;
满足上述条件画出的△ABC和 一定全等吗?由此你能得出什么结论?
获取新知
满足条件的两个三角形不一定全等,由此得出:两边分别相等且其中一组等边的对角相等的两个三角形不一定全等.
(2) ∠A=∠A′= 80°,∠B=∠B′= 30°, ∠C=∠C′=70°.
满足上述条件画出的△ABC和 一定全等吗?由此你能得出什么结论?
满足条件的两个三角形不一定全等,由此得出:三角分别相等的两个三角形不一定全等.
例1 已知:如图,AC与BD相交于点O,且AB= DC,AC = DB.
求证:∠A =∠D.
证明 连接BC.
在△ABC和△DCB中,
∴ △ABC ≌△DCB (SSS).
∴ ∠A =∠D.
AB = DC,
BC = CB (公共边),
AC = DB ,
例题讲解
例2 已知:如图,AB=CD,BC=DA,E,F是AC上的两点,且AE=CE.求证:BF=DE.
D
C
A
B
E
F
证明:在△ABC和△CDA中,
∴ △ABC≌△CDA(SSS).
AB = CD,
BC = DA ,
AC = CA (公共边),
∴ ∠BCF=∠DAE
在△BCF和△DAE中,
∴ △BCF≌△DAE(SAS).
BC = DA ,
∠BCF=∠DAE
CF = AE ,
∴ BF=DE.
例3 某地在山区修建高速公路时需挖通一条隧道. 为估测这条隧道的长度(如图),需测出这座山A,B间的距离,结合所学知识,你能给出什么好方法吗?
解 选择某一合适的地点O,
使得从O点能测出AO与BO的长度.
这样就构造出两个三角形.
连接AO并延长至A′,使 ;
连接BO并延长至B′,使 ,
连接 ,
O
A′
B′
在△AOB和 中,
,
,
,
∴ △AOB≌ (SAS).
∴ AB =
因此只要测出 的长度就能得到这座山A,B间的距离.
1. 已知:如图,AB=AD,BC=DC. 求证:∠B =∠D.
证明 如图,连接AC.
所以 △ACB≌△ ACD (SSS).
所以 ∠B =∠D.
在△ACB和△ACD中,
AB = AD,
BC = CD ,
AC = AC (公共边) ,
随堂演练
2. 如图,在△ABC和△DEC中,已知一些相等的边或角(见下表),请再补充适当的条件,从而能运用已学的判定方法来判定△ABC≌△DEC.
已知条件 补充条件 判定方法
AC=DC,∠A=∠D SAS
∠A=∠D,AB=DE ASA
∠A=∠D,AB=DE AAS
AC=DC,AB=DE SSS
AB=DE
∠B=∠E
∠ACB=∠DCE
BC=EC
3. 如图,在△ABC与△DEF中,已知条件AB=DE,还需添加两个条件才能使△ABC≌△DEF,不能添加的一组条件是( ).
A.∠B=∠E,BC=EF B. BC=EF,AC=DF
C. ∠A=∠D,∠B=∠E D. ∠A=∠D,BC=EF
AB=DE,∠A=∠D,BC=EF 但△ABC与△DEF不全等.
解
D
4. 如图4.2-2,△ACB≌△ ,∠BCB′=30°,则∠ACA′的度数为( ).
A.20° B. 30° C. 35° D. 40°
B
解
∵△ACB≌△ ,
∴ ,
∴ .
故选B.
D
解析:
正确理解运用“SSA”不能判定两个三角形全等:
(1)弄清“SAS”和“SSA”的区别和联系;
(2)不要凭直觉判定两个三角形全等,即使图中所画的两个三角形的确全等,但只要条件是“SSA”,就不能得出全等的结论.
课堂小结
对应相等的元素 两边一角 两角一边 三角 三边
两边及其夹角 两边及其中一边的对角 两角及其夹边 两角及其中一角的对边 三角形是否全等
一定
(SAS)
不一定
一定
(ASA)
一定
(AAS)
不一定
一定
(SSS)
判定三角形全等至少有一组边
同课章节目录
