湘教版数学八年级上册同步课件:2.6 已知两边及其夹角、两角及其夹边作三角形 (第2课时)(共13张PPT)
文档属性
| 名称 | 湘教版数学八年级上册同步课件:2.6 已知两边及其夹角、两角及其夹边作三角形 (第2课时)(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 301.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 15:48:05 | ||
图片预览



文档简介
(共13张PPT)
第二章 三角形
2.6 第2课时 已知两边及其夹角、两角及其夹边作三角形
情景引入
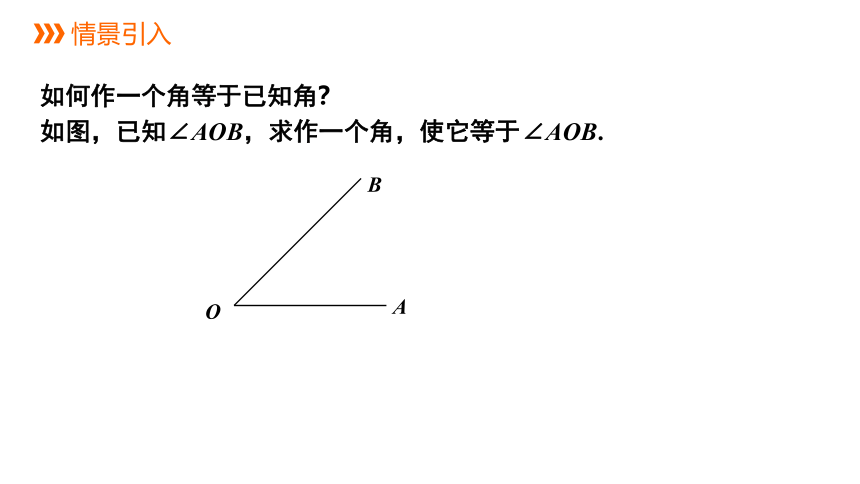
如何作一个角等于已知角?
如图,已知∠AOB,求作一个角,使它等于∠AOB.
O
A
B
1、作射线O′A′。
2、以点O为圆心,以任意长为半径作弧,交OA于点C,交OB于D。
3、以点O′为圆心,以OC长为半径作弧,交O′A′于点C′。
4、以点C′为圆心,以CD长为半径作弧,交前弧于D′。
5、过点D′作射线O′B′。
∠A′O′B′就是所求的角。
O
A
B
C
D
O′
A′
C′
D′
B′
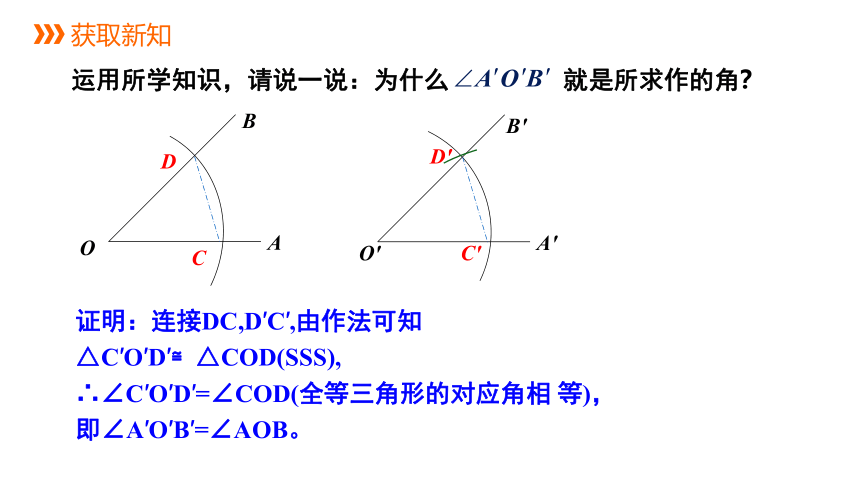
运用所学知识,请说一说:为什么 就是所求作的角?
O
A
B
C
D
O′
A′
C′
D′
B′
证明:连接DC,D′C′,由作法可知
△C′O′D′≌△COD(SSS),
∴∠C′O′D′=∠COD(全等三角形的对应角相 等),
即∠A′O′B′=∠AOB。
获取新知
如图,已知 和线段a, c.
求作△ABC,使 ,BC=a,BA=c.
已知两边及其夹角作三角形.
a
c
例题讲解
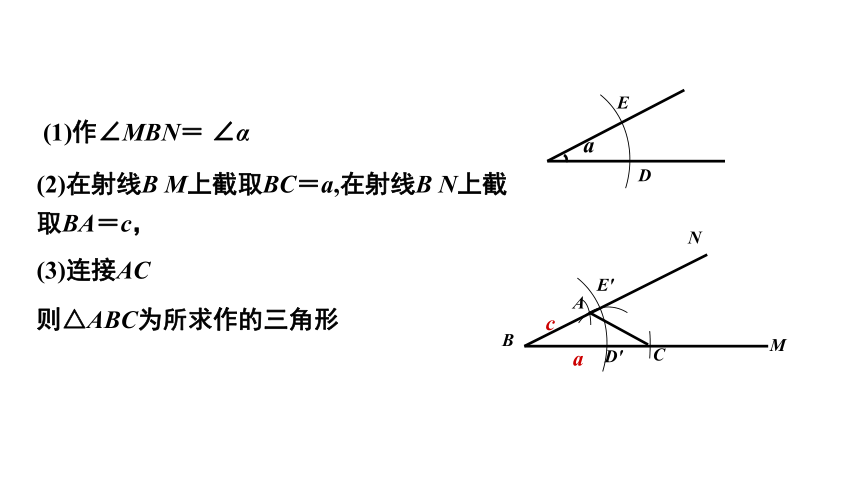
(1)作∠MBN= ∠α
a
D
E
B
M
D′
E′
N
(2)在射线B M上截取BC=a,在射线B N上截取BA=c,
C
A
a
c
(3)连接AC
则△ABC为所求作的三角形
已知两边及其夹角作三角形的两种思路:
思路一:
(1)先作一角等于已知角;
(2)再在作出的角的两边上分别截取线段长等于已知的边长;
(3)连接两个端点,即得所求作的三角形.
思路二:
(1)先作一边;
(2)再以所作边的一个端点为顶点,所作边为边作一个角等于已知角;
(3)在所作角的另一边上截取一条线段等于另一边长,连接两个端点,即得所求作的三角形.
如图,已知 , 和线段a .
求作△ABC,使 , ,BC = a.
已知两角及其夹边作三角形.
β
a
α
作法:(1)作线段BC=a
B
M
C
D
E
A
(3)作∠ECB=∠β
(2)作∠DBC=∠α,
BD与CE相交于A,则△ABC为所求作的三角形
用尺规完成下列作图(只保留作图痕迹,不要求写出作法).
1. 用尺规作一个角等于90°.
如图所示,
①在直线l上截取线段PA、PB,使PA=PB;
②分别以点A、B为圆心,大于PA的任意长度为半径画弧,两弧相交于点C.
③连接CP,则∠CPA= ∠CPB= 90°.
2. 如图,已知线段a,b,求作一个直角三角形,使它的两直角边分别为a和b.
如图所示,
①作∠MCN=90°.
②在射线CM上截取CA=a,
在射线CN上截取CB=b.
③连接AB,则△ABC就是所求作的三角形.
a
b
a
b
②③①④
答案不唯一,如:已知AC或∠B
课堂小结
知识点一 作一个角等于已知角
知识点二 已知两边及其夹角作三角形
已知角
边长
知识点三 已知两角及其夹边作三角形
已知线段
同旁
等于已知的两个角
第二章 三角形
2.6 第2课时 已知两边及其夹角、两角及其夹边作三角形
情景引入
如何作一个角等于已知角?
如图,已知∠AOB,求作一个角,使它等于∠AOB.
O
A
B
1、作射线O′A′。
2、以点O为圆心,以任意长为半径作弧,交OA于点C,交OB于D。
3、以点O′为圆心,以OC长为半径作弧,交O′A′于点C′。
4、以点C′为圆心,以CD长为半径作弧,交前弧于D′。
5、过点D′作射线O′B′。
∠A′O′B′就是所求的角。
O
A
B
C
D
O′
A′
C′
D′
B′
运用所学知识,请说一说:为什么 就是所求作的角?
O
A
B
C
D
O′
A′
C′
D′
B′
证明:连接DC,D′C′,由作法可知
△C′O′D′≌△COD(SSS),
∴∠C′O′D′=∠COD(全等三角形的对应角相 等),
即∠A′O′B′=∠AOB。
获取新知
如图,已知 和线段a, c.
求作△ABC,使 ,BC=a,BA=c.
已知两边及其夹角作三角形.
a
c
例题讲解
(1)作∠MBN= ∠α
a
D
E
B
M
D′
E′
N
(2)在射线B M上截取BC=a,在射线B N上截取BA=c,
C
A
a
c
(3)连接AC
则△ABC为所求作的三角形
已知两边及其夹角作三角形的两种思路:
思路一:
(1)先作一角等于已知角;
(2)再在作出的角的两边上分别截取线段长等于已知的边长;
(3)连接两个端点,即得所求作的三角形.
思路二:
(1)先作一边;
(2)再以所作边的一个端点为顶点,所作边为边作一个角等于已知角;
(3)在所作角的另一边上截取一条线段等于另一边长,连接两个端点,即得所求作的三角形.
如图,已知 , 和线段a .
求作△ABC,使 , ,BC = a.
已知两角及其夹边作三角形.
β
a
α
作法:(1)作线段BC=a
B
M
C
D
E
A
(3)作∠ECB=∠β
(2)作∠DBC=∠α,
BD与CE相交于A,则△ABC为所求作的三角形
用尺规完成下列作图(只保留作图痕迹,不要求写出作法).
1. 用尺规作一个角等于90°.
如图所示,
①在直线l上截取线段PA、PB,使PA=PB;
②分别以点A、B为圆心,大于PA的任意长度为半径画弧,两弧相交于点C.
③连接CP,则∠CPA= ∠CPB= 90°.
2. 如图,已知线段a,b,求作一个直角三角形,使它的两直角边分别为a和b.
如图所示,
①作∠MCN=90°.
②在射线CM上截取CA=a,
在射线CN上截取CB=b.
③连接AB,则△ABC就是所求作的三角形.
a
b
a
b
②③①④
答案不唯一,如:已知AC或∠B
课堂小结
知识点一 作一个角等于已知角
知识点二 已知两边及其夹角作三角形
已知角
边长
知识点三 已知两角及其夹边作三角形
已知线段
同旁
等于已知的两个角
同课章节目录
