湘教版数学八年级上册同步课件:3.1 第2课时 无理数(共18张PPT)
文档属性
| 名称 | 湘教版数学八年级上册同步课件:3.1 第2课时 无理数(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第三章 实数
3.1 第2课时 无理数
情景引入
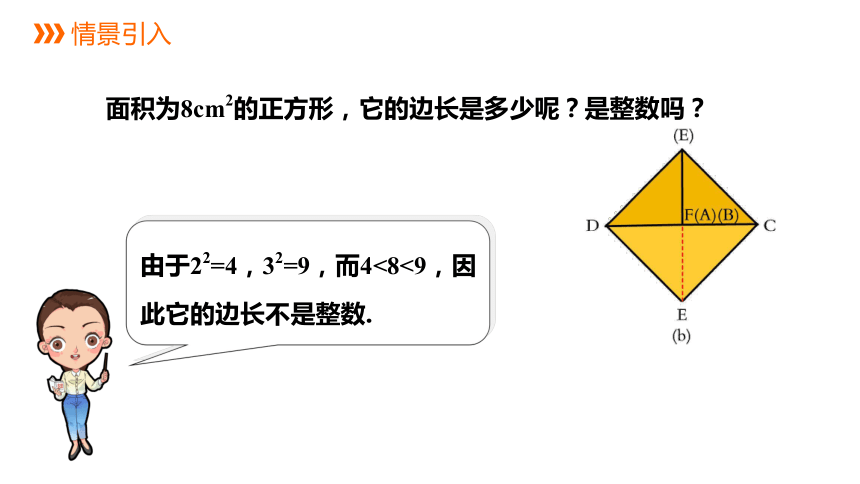
面积为8cm2的正方形,它的边长是多少呢?是整数吗?
由于22=4,32=9,而4<8<9,因此它的边长不是整数.
它的边长是小数吗?观察下列结果(学生也可以用计算器自己运算):
2.82=7.84, 2.92=8.41;
2.822=7.9524 2.832=8.0089
2.8282=7.997584 2.8292=8.003241
2.82842=7.99984656 2.82852=8.00041225
正方形的边长比2.8大,比2.9小;比2.828大,比2.829小;比2.8284大,比2.8285小;······
从上述数据,你能看出什么?
由刚才的推理过程你能发现什么规律?
有些数的小数部分是无限的.
如何确定这些数的大小?
可用两个数去无限地逼近这个数,从而得到相对精确的取值范围.
2.82=7.84, 2.92=8.41;
2.822=7.9524 2.832=8.0089
2.8282=7.997584 2.8292=8.003241
2.82842=7.99984656 2.82852=8.00041225
由此猜想,面积为8cm2的正方形,它的边长是一个小数点后面的位数可以不断增加的小数.
我们也可以说明这个边长不是分数,从而它既不是有限小数,也不是无限循环小数. 这种小数叫作无限不循环小数.
我们把无限不循环小数叫作无理数.
获取新知
由于正方形的边长的平方等于它的面积,因此面积为8cm2的正方形的边长可以记作 .
从上述分析知道, 是一个无限不循环小数,因此 是一个无理数.
与有理数一样,无理数也有正负之分,
例如, , , 是正无理数,
, , 是负无理数.
圆周率π=3.14159265…是无限不循环小数,
除此外, , , ,…也都是无理数.
因此π 也是一个无理数.
1.无理数的三种表现形式:
(1)开方开不尽的数,如√2,-√5, 2, 3等;
(2)具有特定意义的数,如π等;
(3)具有特殊结构的数,如5.252252225…(相邻两个5之间依次多一个2)等.
2.有理数、无理数的区别:
有理数都可以化成小数,其中整数可以看作小数点后面是零的小数,如2=2.0,分数都可以化为有限小数或无限循环小数,如1/3=0.3┴" " ;无理数不能化成小数.
根据实际需要,我们往往用一个有限小数来近似地表示一个无理数.
例如 …,用四舍五入法,分别取到小数点后面第二位,第三位,…,得到 , ,…,我们称3.14,3.142是 的精确到小数点后面第二位,第三位的近似值.
3.14,3.142,3.141 6,…都是 的近似值,称它们为近似数.
小知识
最早被发现的无理数是 .公元前5世纪,毕达哥拉斯学派的一个成员发现边长为1的正方形的对角线的长不能用整数或整数之比来表示,从而它是无理数.
我们可以用计算器求一个正数a的平方根,其操作方法是按顺序进行按键输入:
例1 用计算器求 的近似值(用四舍五入法取到小数点后面第三位).
按键 ,
显示:2.828457125
所以,
解:
例题讲解
用计算器计算下列各式的值.
(1) (2)
解:
用计算器计算 ,
显示:56
所以,
用计算器计算 ,
显示:1.24
所以,
随堂演练
2.面积为6cm2的正方形,它的边长是多少?用计算器求边长的近似值(精确到0.001cm)?
正方形的面积是6cm2,
因此它的边长为 cm.
解:
用计算器计算 :显示2.4494897
所以,边长的近似值为2.449cm .
3. 用计算器分别求 , , , , ,的近似值(精确到0.001).
解:
4.用计算器分别计算:
解
5.用计算器分别求 , 的近似值(精确到0.001).
解
无理数与有理数的区别与联系是什么?
实数应该如何分类?
如何用计算器计算一个非负数的算术平方根?
如何估计一个无理数的大小?
课堂小结
第三章 实数
3.1 第2课时 无理数
情景引入
面积为8cm2的正方形,它的边长是多少呢?是整数吗?
由于22=4,32=9,而4<8<9,因此它的边长不是整数.
它的边长是小数吗?观察下列结果(学生也可以用计算器自己运算):
2.82=7.84, 2.92=8.41;
2.822=7.9524 2.832=8.0089
2.8282=7.997584 2.8292=8.003241
2.82842=7.99984656 2.82852=8.00041225
正方形的边长比2.8大,比2.9小;比2.828大,比2.829小;比2.8284大,比2.8285小;······
从上述数据,你能看出什么?
由刚才的推理过程你能发现什么规律?
有些数的小数部分是无限的.
如何确定这些数的大小?
可用两个数去无限地逼近这个数,从而得到相对精确的取值范围.
2.82=7.84, 2.92=8.41;
2.822=7.9524 2.832=8.0089
2.8282=7.997584 2.8292=8.003241
2.82842=7.99984656 2.82852=8.00041225
由此猜想,面积为8cm2的正方形,它的边长是一个小数点后面的位数可以不断增加的小数.
我们也可以说明这个边长不是分数,从而它既不是有限小数,也不是无限循环小数. 这种小数叫作无限不循环小数.
我们把无限不循环小数叫作无理数.
获取新知
由于正方形的边长的平方等于它的面积,因此面积为8cm2的正方形的边长可以记作 .
从上述分析知道, 是一个无限不循环小数,因此 是一个无理数.
与有理数一样,无理数也有正负之分,
例如, , , 是正无理数,
, , 是负无理数.
圆周率π=3.14159265…是无限不循环小数,
除此外, , , ,…也都是无理数.
因此π 也是一个无理数.
1.无理数的三种表现形式:
(1)开方开不尽的数,如√2,-√5, 2, 3等;
(2)具有特定意义的数,如π等;
(3)具有特殊结构的数,如5.252252225…(相邻两个5之间依次多一个2)等.
2.有理数、无理数的区别:
有理数都可以化成小数,其中整数可以看作小数点后面是零的小数,如2=2.0,分数都可以化为有限小数或无限循环小数,如1/3=0.3┴" " ;无理数不能化成小数.
根据实际需要,我们往往用一个有限小数来近似地表示一个无理数.
例如 …,用四舍五入法,分别取到小数点后面第二位,第三位,…,得到 , ,…,我们称3.14,3.142是 的精确到小数点后面第二位,第三位的近似值.
3.14,3.142,3.141 6,…都是 的近似值,称它们为近似数.
小知识
最早被发现的无理数是 .公元前5世纪,毕达哥拉斯学派的一个成员发现边长为1的正方形的对角线的长不能用整数或整数之比来表示,从而它是无理数.
我们可以用计算器求一个正数a的平方根,其操作方法是按顺序进行按键输入:
例1 用计算器求 的近似值(用四舍五入法取到小数点后面第三位).
按键 ,
显示:2.828457125
所以,
解:
例题讲解
用计算器计算下列各式的值.
(1) (2)
解:
用计算器计算 ,
显示:56
所以,
用计算器计算 ,
显示:1.24
所以,
随堂演练
2.面积为6cm2的正方形,它的边长是多少?用计算器求边长的近似值(精确到0.001cm)?
正方形的面积是6cm2,
因此它的边长为 cm.
解:
用计算器计算 :显示2.4494897
所以,边长的近似值为2.449cm .
3. 用计算器分别求 , , , , ,的近似值(精确到0.001).
解:
4.用计算器分别计算:
解
5.用计算器分别求 , 的近似值(精确到0.001).
解
无理数与有理数的区别与联系是什么?
实数应该如何分类?
如何用计算器计算一个非负数的算术平方根?
如何估计一个无理数的大小?
课堂小结
同课章节目录
