湘教版数学八年级上册同步课件:4.3 一元一次不等式的解集 (第2课时)(共15张PPT)
文档属性
| 名称 | 湘教版数学八年级上册同步课件:4.3 一元一次不等式的解集 (第2课时)(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 269.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
4.3 第2课时 在数轴上表示一元一次不等式的解集
第四章 一元一次不等式(组)
情景引入
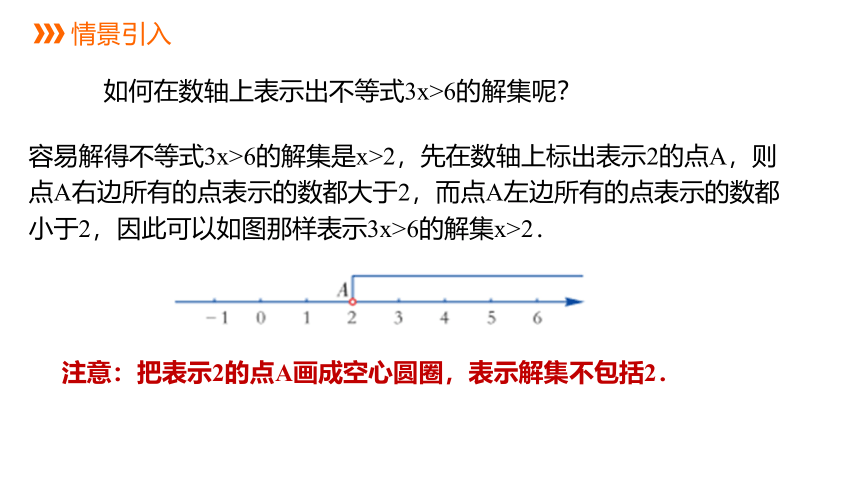
如何在数轴上表示出不等式3x>6的解集呢?
容易解得不等式3x>6的解集是x>2,先在数轴上标出表示2的点A,则点A右边所有的点表示的数都大于2,而点A左边所有的点表示的数都小于2,因此可以如图那样表示3x>6的解集x>2.
注意:把表示2的点A画成空心圆圈,表示解集不包括2.
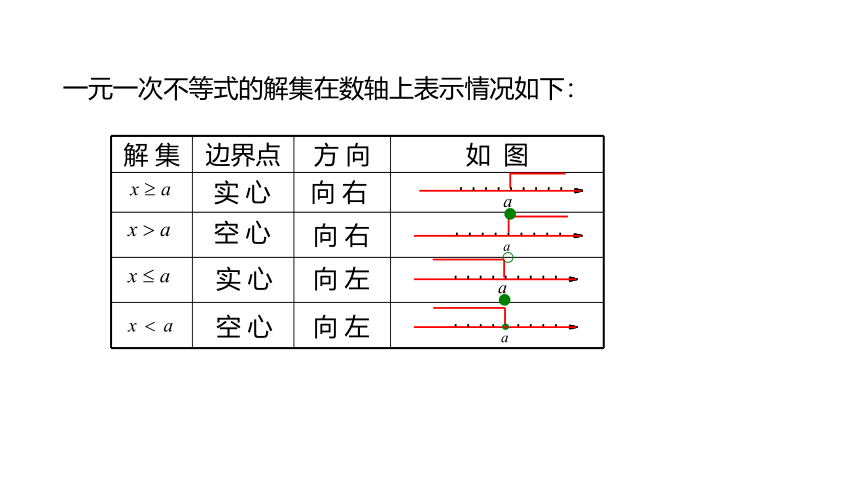
一元一次不等式的解集在数轴上表示情况如下:
解 集 边界点 方 向 如 图
空 心
实 心
空 心
实 心
向 左
向 左
向 右
向 右
●
○
●
例2 解不等式12-6x≥2(1-2x),并把它的解集在数轴上表示出来 :
解
首先将括号去掉
去括号,得 12 -6x ≥ 2-4x
移项,得 -6x+4x ≥ 2-12
将同类项放在一起
合并同类项,得: -2x ≥ -10
两边都除以-2,得 x ≤ 5
根据不等式基本性质2
原不等式的解集在数轴上表示如图所示.
-1
0
1
2
3
4
5
6
解集x≤5中包含5,所以在数轴上将表示5的点画成实心圆点.
例题讲解
解
解这个不等式,得 x ≤ 6
x≤6在数轴上表示如图所示:
-1
0
1
2
3
4
5
6
根据题意,得 x +2≥ 0
所以,当x≤6时,代数式 x+2的值大于或等于0.
由图可知,满足条件的正整数有 1,2,3,4,5,6.
例3 当x取什么值时,代数式 x+2的值大于或等于0?并求出所有满足条件的正整数.
小知识
(1)在步骤①“去分母”和⑤“未知数的系数化成1”中,如果乘数或除数是负数,要把不等号改变方向.
(2)一元一次不等式的解集含有无限多个数.
(3)变形中,要避免解方程中易出现的错误在解不等式中重现.(强调一下例题中指出的应注意的问题).要灵活运用五个步骤.
解一元一次不等式的注意事项:
①利用数轴法;
②直接比较法;
③差值比较法;
④商值比较法;
⑤利用特殊比较法.
注意:在涉及代数式的比较时,还要适当的使用分类讨论法.
代数式大小的比较:
随堂演练
1. 解下列不等式,并把它们的解集在数轴上表示出来:
(1) 4x -3 < 2x+7 ;
(2) .
解
(1) 原不等式为 4x -3 < 2x+7
移项,得 4x-2x < 3+7
化简,得 2x < 10
两边同除以2, x < 5
原不等式的解集在数轴上表示为:
-1
0
1
2
3
4
5
6
(2) 原不等式为
去分母,得 2(x-3)≥ (3x+5)
去括号,得 2x-6 ≥ 3x+5
移项,得 2x -3x ≥ 6+5
化简,得 -x ≥ 11
两边同除以 -1, x ≤-11
原不等式的解集在数轴上表示为:
0
-11
2. 先用不等式表示下列数量关系,然后求出它们的解集,并在数轴上表示出来:
(1) x的 大于或等于2;
-1
0
1
2
3
4
5
x ≥ 2
解得 x ≥ 4
解
(2) x与2的和不小于1;
解
x+2 ≥ 1
解得 x ≥ -1
-1
0
1
2
3
4
5
y-1 ≤ 0
解得 y ≤ 1
解
-1
0
1
2
3
4
5
(3) y与1的差不大于0;
(4) y与5的差大于-2;
y-5 > -2
解得 y > 3
解
-1
0
1
2
3
4
5
去分母,得 6+3x≥4x+2.
移项,合并同类项,得 x≤4.
正整数解为 1,2,3,4.
解
3.求不等式 的正整数解.
首先求出不等式的解集.然后求出正整数解.
分析
4.已知 且x>y,则k的取值范围是 .
解
∵
①×3-②×2,得 x = 7k+5 . ③
将③代入① ,得
3(7k+5)-2y=3k+1.
化简,整理,得 y=9k+7.
∵ x > y,
∴ 7k+5>9k+7.解之,得k<-1.
①
②
k<-1
5.解不等式 ,并把解集在数轴上表示出来.
-2
-1
0
1
2
3
4
去分母,得 6(2x-1)≥10x+1.
去括号,移项,合并同类项得 2x≥7.
解得
这个不等式的解集在数轴上表示如下图:
解
(1)解一元一次方程的依据是什么?
等式的基本性质
(2)解一元一次不等式的依据是什么?
不等式的基本性质
(3)两者有什么区别?
不等式的左右两边同时乘以或除以同一个负数,不等号的方向改变
(4)解一元一次方程和一元一次不等式的一般步骤?
去分母、去括号、移项、合并同类项、化系数为1
课堂小结
4.3 第2课时 在数轴上表示一元一次不等式的解集
第四章 一元一次不等式(组)
情景引入
如何在数轴上表示出不等式3x>6的解集呢?
容易解得不等式3x>6的解集是x>2,先在数轴上标出表示2的点A,则点A右边所有的点表示的数都大于2,而点A左边所有的点表示的数都小于2,因此可以如图那样表示3x>6的解集x>2.
注意:把表示2的点A画成空心圆圈,表示解集不包括2.
一元一次不等式的解集在数轴上表示情况如下:
解 集 边界点 方 向 如 图
空 心
实 心
空 心
实 心
向 左
向 左
向 右
向 右
●
○
●
例2 解不等式12-6x≥2(1-2x),并把它的解集在数轴上表示出来 :
解
首先将括号去掉
去括号,得 12 -6x ≥ 2-4x
移项,得 -6x+4x ≥ 2-12
将同类项放在一起
合并同类项,得: -2x ≥ -10
两边都除以-2,得 x ≤ 5
根据不等式基本性质2
原不等式的解集在数轴上表示如图所示.
-1
0
1
2
3
4
5
6
解集x≤5中包含5,所以在数轴上将表示5的点画成实心圆点.
例题讲解
解
解这个不等式,得 x ≤ 6
x≤6在数轴上表示如图所示:
-1
0
1
2
3
4
5
6
根据题意,得 x +2≥ 0
所以,当x≤6时,代数式 x+2的值大于或等于0.
由图可知,满足条件的正整数有 1,2,3,4,5,6.
例3 当x取什么值时,代数式 x+2的值大于或等于0?并求出所有满足条件的正整数.
小知识
(1)在步骤①“去分母”和⑤“未知数的系数化成1”中,如果乘数或除数是负数,要把不等号改变方向.
(2)一元一次不等式的解集含有无限多个数.
(3)变形中,要避免解方程中易出现的错误在解不等式中重现.(强调一下例题中指出的应注意的问题).要灵活运用五个步骤.
解一元一次不等式的注意事项:
①利用数轴法;
②直接比较法;
③差值比较法;
④商值比较法;
⑤利用特殊比较法.
注意:在涉及代数式的比较时,还要适当的使用分类讨论法.
代数式大小的比较:
随堂演练
1. 解下列不等式,并把它们的解集在数轴上表示出来:
(1) 4x -3 < 2x+7 ;
(2) .
解
(1) 原不等式为 4x -3 < 2x+7
移项,得 4x-2x < 3+7
化简,得 2x < 10
两边同除以2, x < 5
原不等式的解集在数轴上表示为:
-1
0
1
2
3
4
5
6
(2) 原不等式为
去分母,得 2(x-3)≥ (3x+5)
去括号,得 2x-6 ≥ 3x+5
移项,得 2x -3x ≥ 6+5
化简,得 -x ≥ 11
两边同除以 -1, x ≤-11
原不等式的解集在数轴上表示为:
0
-11
2. 先用不等式表示下列数量关系,然后求出它们的解集,并在数轴上表示出来:
(1) x的 大于或等于2;
-1
0
1
2
3
4
5
x ≥ 2
解得 x ≥ 4
解
(2) x与2的和不小于1;
解
x+2 ≥ 1
解得 x ≥ -1
-1
0
1
2
3
4
5
y-1 ≤ 0
解得 y ≤ 1
解
-1
0
1
2
3
4
5
(3) y与1的差不大于0;
(4) y与5的差大于-2;
y-5 > -2
解得 y > 3
解
-1
0
1
2
3
4
5
去分母,得 6+3x≥4x+2.
移项,合并同类项,得 x≤4.
正整数解为 1,2,3,4.
解
3.求不等式 的正整数解.
首先求出不等式的解集.然后求出正整数解.
分析
4.已知 且x>y,则k的取值范围是 .
解
∵
①×3-②×2,得 x = 7k+5 . ③
将③代入① ,得
3(7k+5)-2y=3k+1.
化简,整理,得 y=9k+7.
∵ x > y,
∴ 7k+5>9k+7.解之,得k<-1.
①
②
k<-1
5.解不等式 ,并把解集在数轴上表示出来.
-2
-1
0
1
2
3
4
去分母,得 6(2x-1)≥10x+1.
去括号,移项,合并同类项得 2x≥7.
解得
这个不等式的解集在数轴上表示如下图:
解
(1)解一元一次方程的依据是什么?
等式的基本性质
(2)解一元一次不等式的依据是什么?
不等式的基本性质
(3)两者有什么区别?
不等式的左右两边同时乘以或除以同一个负数,不等号的方向改变
(4)解一元一次方程和一元一次不等式的一般步骤?
去分母、去括号、移项、合并同类项、化系数为1
课堂小结
同课章节目录
