18.2.3正方形课件2021—2022学年人教版数学八年级下册 (共21张PPT)
文档属性
| 名称 | 18.2.3正方形课件2021—2022学年人教版数学八年级下册 (共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 652.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 16:21:32 | ||
图片预览






文档简介
(共21张PPT)
18.2.3 正方形
丰富多彩的正方形
一、再识正方形
1、你对正方形有哪些认识?
2、你的生活中有用到正方形图案吗?
我们学行四边形、矩形、菱形、正方形等特殊的四边形,在这些特殊的四边形中,正方形无疑是最美、性质最多的四边形。
丰富多彩的正方形
实践出真知
A
B
C
D
E
F
G
H
P
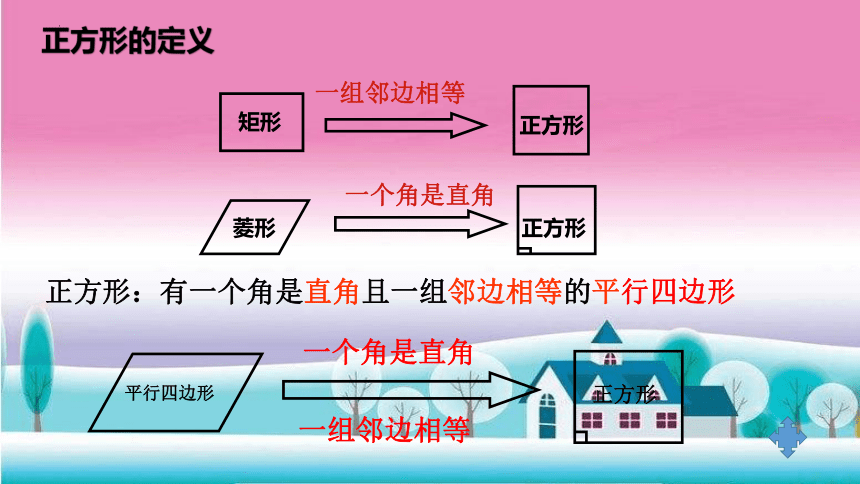
正方形:有一个角是直角且一组邻边相等的平行四边形
正方形的定义
一个角是直角
正方形
一组邻边相等
平行四边形
正方形
一个角是直角
菱形
正方形
一组邻边相等
矩形
探索与思考
结合之前所学知识,你知道正方形有哪些特殊性质吗?你知道正方形与矩形、菱形和平行四边形之间的关系吗?
四条边相等,四个角都是直角
矩形
邻边相等
一组邻边相等的矩形是正方形
菱形
一个角是直角
一个角为直角的菱形是正方形
正方形的性质
正方形的四个角都是直角,四条边都相等
正方形的两条对角线相等,并且互相垂直平分、每条对角线平分一组对角
A
B
C
D
O
想一想
正方形的两条对角线将其分成了什么三角形?
探索与思考
正方形的两条对角线把正方形分成四个全等的等腰直角三角形。
已知: 如图,四边形ABCD是正方形,对角线AC、BD相交于点O。
求证: △ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形。
A
D
C
B
O
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,
并且△ABO≌△BCO≌△CDO≌△DAO
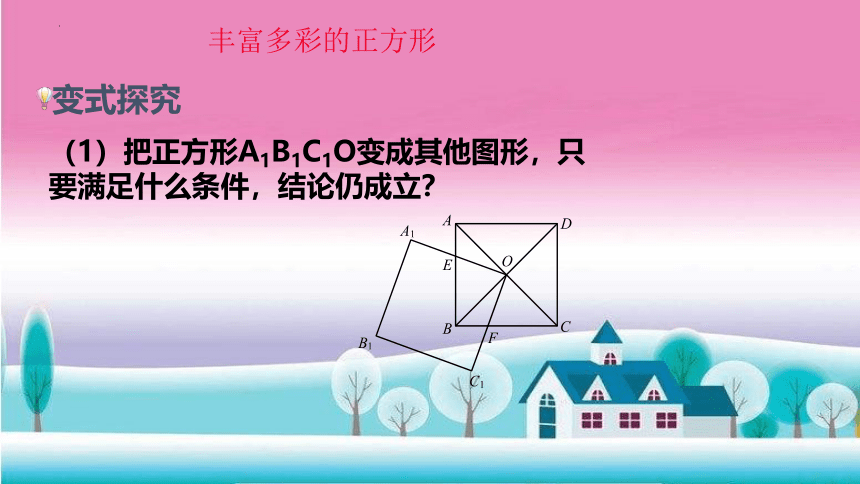
丰富多彩的正方形
变式探究
(1)把正方形A1B1C1O变成其他图形,只要满足什么条件,结论仍成立?
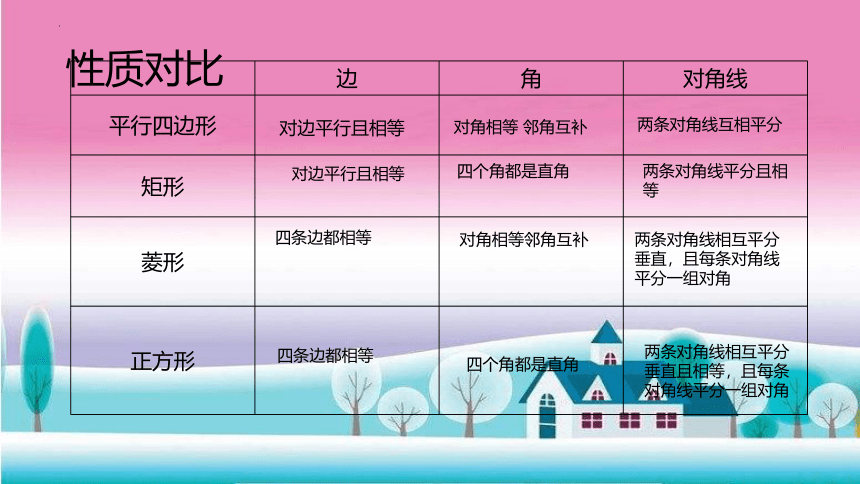
性质对比
边 角 对角线
平行四边形
矩形
菱形
正方形
对边平行且相等
对角相等 邻角互补
两条对角线互相平分
对边平行且相等
四个角都是直角
两条对角线平分且相等
四条边都相等
对角相等邻角互补
两条对角线相互平分垂直,且每条对角线平分一组对角
四条边都相等
四个角都是直角
两条对角线相互平分垂直且相等,且每条对角线平分一组对角
课堂测试(理解正方形的性质)
对正方形的描述错误的是( )
A.正方形的四个角都是直角 B.正方形的对角线互相垂直
C.邻边相等的矩形是正方形 D.对角线相等的平行四边形是正方形
【详解】
解:∵正方形的四个角都是直角,对角线互相垂直,∴A、B正确;
∵邻边相等的矩形是正方形,∴C正确;
∵对角线相等的平行四边形是矩形,不一定是正方形,∴D不正确;
故选D.
丰富多彩的正方形
反馈训练
1、如图,用边长为1的正方形,制成一副七巧板,将它拼成“小天鹅”图案,其中阴影部分的面积是________.
求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
这是一道文字证明题,该怎么做 你会做吗
第一步:根据题意画出图形
第二步:写出已知、求证
第三步:进行证明
A
D
C
B
O
已知:如图,四边形ABCD是正方形,对 角线AC、BD相交于点O.
求证:△ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO
分析:利用正方形的性质,对角线互相垂直平分且相等,每条对角线平分一组对角.平分可以产生线段等量关系,垂直可以产生直角,于是可以得到四个全等的等腰直角三角形.
课堂测试(理解正方形的性质)
如图,将矩形纸片ABCD折叠,使点A落在BC上的点F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是( )
A.邻边相等的矩形是正方形
B.对角线相等的菱形是正方形
C.两个全等的直角三角形构成正方形
D.轴对称图形是正方形
【解析】
∵将长方形纸片折叠,A落在BC上的F处,∴BA=BF,
∵折痕为BE,沿EF剪下,∴四边形ABFE为矩形,
∴四边形ABEF为正方形.
故用的判定定理是;邻边相等的矩形是正方形.故选A.
丰富多彩的正方形
反馈训练
(2)请你继续完成下面的探索:
①将图甲中的正方形ACDE绕点C顺时针旋转任意角度(如图乙),那么AF与BD的关系是_________;
②当点C运动到直线AB上方时,如图丙,连接DF、AD、BF,取DF、AD、AB、BF的中点M、N、P、H,得到的四边形MNPH是什么图形?
1.操作:将一张矩形纸片沿图18-2-30中所示的箭头方向折叠,然后沿虚线剪开,所得的四边形ABCD是___________.
图18-2-30
正方形
如果给你一张矩形的纸,你能裁剪出一个正方形吗?
请动手试一试。
一个角是直角的菱形是正方形
课堂测试(利用正方形的性质进行计算)
如图,在正方形ABCD的外侧,作等边三角形ADE,则∠BED为( )
A.45° B.15° C.10° D.125°
【详解】
是等边三角形,
,,
四边形是正方形,
,,
,,
,
.
故选:.
利用正方形的性质进行计算
如图,在正方形ABCD中,,点E在对角线AC上,若,则CDE的面积为( )
A.3 B.4 C.5 D.6
【详解】
∵正方形ABCD,
∴AB=AD,∠BAC=DAC,
∵AE=AE,∴△ABE≌△ADE,
∴=5,同理△CBE≌△CDE,
∴,
∵,
∴CDE的面积为: =3,
故选A.
例3如图,已知平行四边形ABCD中,对角线AC,BD相交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
有一组邻边相等
且有一个角是直角
的平行四边形
叫做正方形。
平行四边形
有一个直角
矩形
一组邻边相等
菱形
一组邻边相等
正方形
有一个直角
有一组邻边相等的矩形是正方形
有一个角为直角的菱形是正方形
特殊的矩形
特殊的菱形
特殊的
平行四边形
一组邻边相等
有一个直角
正方形的判定
课后回顾
理解正方形的概念
01
课后回顾
理解正方形的性质
02
理解正方形的判定
03
同学们,再见
18.2.3 正方形
丰富多彩的正方形
一、再识正方形
1、你对正方形有哪些认识?
2、你的生活中有用到正方形图案吗?
我们学行四边形、矩形、菱形、正方形等特殊的四边形,在这些特殊的四边形中,正方形无疑是最美、性质最多的四边形。
丰富多彩的正方形
实践出真知
A
B
C
D
E
F
G
H
P
正方形:有一个角是直角且一组邻边相等的平行四边形
正方形的定义
一个角是直角
正方形
一组邻边相等
平行四边形
正方形
一个角是直角
菱形
正方形
一组邻边相等
矩形
探索与思考
结合之前所学知识,你知道正方形有哪些特殊性质吗?你知道正方形与矩形、菱形和平行四边形之间的关系吗?
四条边相等,四个角都是直角
矩形
邻边相等
一组邻边相等的矩形是正方形
菱形
一个角是直角
一个角为直角的菱形是正方形
正方形的性质
正方形的四个角都是直角,四条边都相等
正方形的两条对角线相等,并且互相垂直平分、每条对角线平分一组对角
A
B
C
D
O
想一想
正方形的两条对角线将其分成了什么三角形?
探索与思考
正方形的两条对角线把正方形分成四个全等的等腰直角三角形。
已知: 如图,四边形ABCD是正方形,对角线AC、BD相交于点O。
求证: △ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形。
A
D
C
B
O
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,
并且△ABO≌△BCO≌△CDO≌△DAO
丰富多彩的正方形
变式探究
(1)把正方形A1B1C1O变成其他图形,只要满足什么条件,结论仍成立?
性质对比
边 角 对角线
平行四边形
矩形
菱形
正方形
对边平行且相等
对角相等 邻角互补
两条对角线互相平分
对边平行且相等
四个角都是直角
两条对角线平分且相等
四条边都相等
对角相等邻角互补
两条对角线相互平分垂直,且每条对角线平分一组对角
四条边都相等
四个角都是直角
两条对角线相互平分垂直且相等,且每条对角线平分一组对角
课堂测试(理解正方形的性质)
对正方形的描述错误的是( )
A.正方形的四个角都是直角 B.正方形的对角线互相垂直
C.邻边相等的矩形是正方形 D.对角线相等的平行四边形是正方形
【详解】
解:∵正方形的四个角都是直角,对角线互相垂直,∴A、B正确;
∵邻边相等的矩形是正方形,∴C正确;
∵对角线相等的平行四边形是矩形,不一定是正方形,∴D不正确;
故选D.
丰富多彩的正方形
反馈训练
1、如图,用边长为1的正方形,制成一副七巧板,将它拼成“小天鹅”图案,其中阴影部分的面积是________.
求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
这是一道文字证明题,该怎么做 你会做吗
第一步:根据题意画出图形
第二步:写出已知、求证
第三步:进行证明
A
D
C
B
O
已知:如图,四边形ABCD是正方形,对 角线AC、BD相交于点O.
求证:△ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO
分析:利用正方形的性质,对角线互相垂直平分且相等,每条对角线平分一组对角.平分可以产生线段等量关系,垂直可以产生直角,于是可以得到四个全等的等腰直角三角形.
课堂测试(理解正方形的性质)
如图,将矩形纸片ABCD折叠,使点A落在BC上的点F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是( )
A.邻边相等的矩形是正方形
B.对角线相等的菱形是正方形
C.两个全等的直角三角形构成正方形
D.轴对称图形是正方形
【解析】
∵将长方形纸片折叠,A落在BC上的F处,∴BA=BF,
∵折痕为BE,沿EF剪下,∴四边形ABFE为矩形,
∴四边形ABEF为正方形.
故用的判定定理是;邻边相等的矩形是正方形.故选A.
丰富多彩的正方形
反馈训练
(2)请你继续完成下面的探索:
①将图甲中的正方形ACDE绕点C顺时针旋转任意角度(如图乙),那么AF与BD的关系是_________;
②当点C运动到直线AB上方时,如图丙,连接DF、AD、BF,取DF、AD、AB、BF的中点M、N、P、H,得到的四边形MNPH是什么图形?
1.操作:将一张矩形纸片沿图18-2-30中所示的箭头方向折叠,然后沿虚线剪开,所得的四边形ABCD是___________.
图18-2-30
正方形
如果给你一张矩形的纸,你能裁剪出一个正方形吗?
请动手试一试。
一个角是直角的菱形是正方形
课堂测试(利用正方形的性质进行计算)
如图,在正方形ABCD的外侧,作等边三角形ADE,则∠BED为( )
A.45° B.15° C.10° D.125°
【详解】
是等边三角形,
,,
四边形是正方形,
,,
,,
,
.
故选:.
利用正方形的性质进行计算
如图,在正方形ABCD中,,点E在对角线AC上,若,则CDE的面积为( )
A.3 B.4 C.5 D.6
【详解】
∵正方形ABCD,
∴AB=AD,∠BAC=DAC,
∵AE=AE,∴△ABE≌△ADE,
∴=5,同理△CBE≌△CDE,
∴,
∵,
∴CDE的面积为: =3,
故选A.
例3如图,已知平行四边形ABCD中,对角线AC,BD相交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
有一组邻边相等
且有一个角是直角
的平行四边形
叫做正方形。
平行四边形
有一个直角
矩形
一组邻边相等
菱形
一组邻边相等
正方形
有一个直角
有一组邻边相等的矩形是正方形
有一个角为直角的菱形是正方形
特殊的矩形
特殊的菱形
特殊的
平行四边形
一组邻边相等
有一个直角
正方形的判定
课后回顾
理解正方形的概念
01
课后回顾
理解正方形的性质
02
理解正方形的判定
03
同学们,再见
