五年级下学期数学4.5.1最小公倍数课件(共19张PPT)
文档属性
| 名称 | 五年级下学期数学4.5.1最小公倍数课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 17:20:47 | ||
图片预览






文档简介
(共19张PPT)
最小公倍数
学习目标
培养利用数学知识解决生活问题的能力,提高数学学习兴趣。
在学会找最小公倍数的过程中,体验数学在实际生活中的应用。
让学生能利用最小公倍数知识解决生活中的实际问题。
结合解决问题理解公倍数和最小公倍数的意义,学会求两个数的最小公倍数的方法。
在探索公倍数和最小公倍数意义的过程中,参加观察、猜测、归纳等数学活动,进一步发展初步的推理能力。在解决问题的过程中,能进行有条理、有根据地进行思考。
学会用公倍数、最小公倍数的知识解决简单的现实问题,体验数学与生活的密切联系。
在探索新知的过程中,培养学好数学的信心以及小组成员之间互相合作的精神。
情境导入
2.一个数的倍数有哪些特征?
一个数最小的倍数是它本身,
没有最大的倍数,
一个数倍数的个数是无限的。
你能说说求两个数的最小公倍数的方法吗?
怎样求8和5的最小公倍数?
先分别写出8和5的倍数,再圈出公有的倍数,从中找到最小公倍数。
8的因数:8,16,24,32,40,48,56,64,72,80……
5的因数: 5,10, 15, 20,25,30,35,40,45,50,55,60,65,70,75,80……
新课讲解
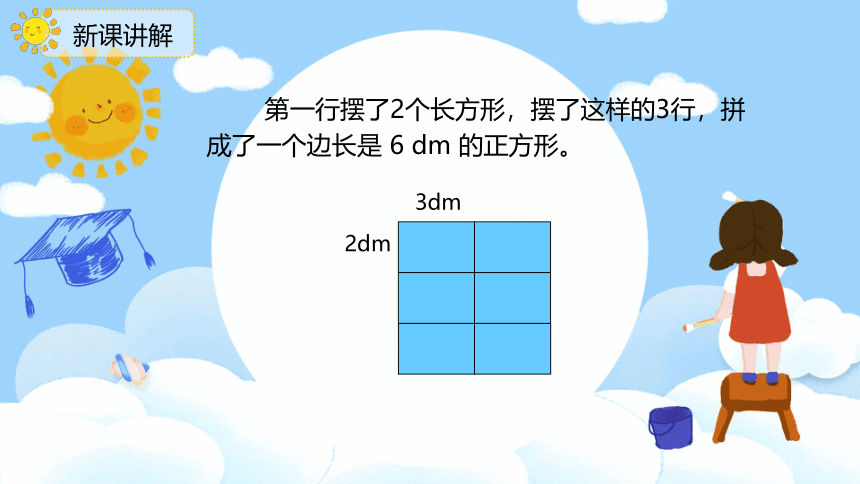
第一行摆了2个长方形,摆了这样的3行,拼成了一个边长是 6 dm 的正方形。
3dm
2dm
还可以这样表示。
4的倍数
6的倍数
4, 8, 16,
20, 28,32, 40, …
6, 18,
30, 42, …
方法二
集合法。
4和6公有的倍数
12, 24, 36,…是4和6公有的倍数,叫做它们的公倍数。其中,12是最小的公倍数,叫做它们的最小公倍数。
4和6公有的倍数有12, 24, 36,… ;公有的最小倍数是12。
12, 24,
36, …
想一想:两个数有没有最大的公倍数?
(教材第68页例1)
回顾与反思
用边长6dm的正方形上画一画,看我找的对不对。
解决这个问题的关键是把铺砖问题转化成求公倍数的问题。
典例精析
新课讲解
怎样求6和8的最小公倍数?
方法一:列举法。
6的倍数:
8的倍数:
6,12,18,24,20,36,42,48,…
8,16,24,32,40,48,…
6和8的最小公倍数是24。
你知道吗?
我们也可以利用分解质因数的方法,比较简便地求出两个数的最小公倍数。例如:
60 =2×2×3×5
42 =2×3×7
60和42的最小公倍数:
2×3×2×5×7 = 420
60
42
2
30
21
3
10
7
…用公有的质因数2除
…用公有的质因数3除
…除到两个商只有公
因数1为止
60和42的最小公倍数:
2×3×10×7 = 420
为了简便,通常写成右侧的形式。
课堂练习
一个数的倍数的个数是无限的。
3. 2和8的最小公倍数是16。
( )
( )
2. 两个数的公倍数有无限个,最小公倍数的个 数只有1个。
( )
√
√
×
2和8的最小公倍数是8。
1.判断题。
求下列每组数的最小公倍数。
2 和 8 3 和 8 6 和 15 6 和 9
4 和 5 1 和 7 4 和 10 8 和 10
8
24
30
18
20
7
20
40
(2)最小的质数和最小的合数的最大公因数是( ),最小公倍数是( )。
(1)12的倍数有( ),9的倍数有( ),12和9的公倍数有( );最小公倍数是( )。
填一填。
(3)两位数“2□”是2和3的公倍数,□里的数字是( )。这个两位数与16的最大公因数是( ),最小公倍数是( )。
12, 24, 36, 48, 60, 72, 84,…
36, 72, …
36
4
2
9, 18, 27, 36, 45, 54, 63, 72, 81, …
4
8
48
课堂练习
3.选一选。 (将正确答案的序号填在括号里)
(1)连续两个自然数( 0除外)的乘积一定是这两 个数的( ).
A.最大公因数 B.最小公倍数 C.公因数
B
3和5 8和9 12和1 4和15
15
72
12
60
你发现了什么?
互质的两个数,它们的最小公倍数是这两个数的乘积。
找出每组数的最小公倍数。
课堂小结
利用公倍数和最小公倍数可以解决生活中的很多问题,如铺地砖问题、学生排队问题、同一天到达问题等等。
课本练习十七第2题、第5题、第12题。
作业布置
Goodbye~
感谢聆听,下期再会
最小公倍数
学习目标
培养利用数学知识解决生活问题的能力,提高数学学习兴趣。
在学会找最小公倍数的过程中,体验数学在实际生活中的应用。
让学生能利用最小公倍数知识解决生活中的实际问题。
结合解决问题理解公倍数和最小公倍数的意义,学会求两个数的最小公倍数的方法。
在探索公倍数和最小公倍数意义的过程中,参加观察、猜测、归纳等数学活动,进一步发展初步的推理能力。在解决问题的过程中,能进行有条理、有根据地进行思考。
学会用公倍数、最小公倍数的知识解决简单的现实问题,体验数学与生活的密切联系。
在探索新知的过程中,培养学好数学的信心以及小组成员之间互相合作的精神。
情境导入
2.一个数的倍数有哪些特征?
一个数最小的倍数是它本身,
没有最大的倍数,
一个数倍数的个数是无限的。
你能说说求两个数的最小公倍数的方法吗?
怎样求8和5的最小公倍数?
先分别写出8和5的倍数,再圈出公有的倍数,从中找到最小公倍数。
8的因数:8,16,24,32,40,48,56,64,72,80……
5的因数: 5,10, 15, 20,25,30,35,40,45,50,55,60,65,70,75,80……
新课讲解
第一行摆了2个长方形,摆了这样的3行,拼成了一个边长是 6 dm 的正方形。
3dm
2dm
还可以这样表示。
4的倍数
6的倍数
4, 8, 16,
20, 28,32, 40, …
6, 18,
30, 42, …
方法二
集合法。
4和6公有的倍数
12, 24, 36,…是4和6公有的倍数,叫做它们的公倍数。其中,12是最小的公倍数,叫做它们的最小公倍数。
4和6公有的倍数有12, 24, 36,… ;公有的最小倍数是12。
12, 24,
36, …
想一想:两个数有没有最大的公倍数?
(教材第68页例1)
回顾与反思
用边长6dm的正方形上画一画,看我找的对不对。
解决这个问题的关键是把铺砖问题转化成求公倍数的问题。
典例精析
新课讲解
怎样求6和8的最小公倍数?
方法一:列举法。
6的倍数:
8的倍数:
6,12,18,24,20,36,42,48,…
8,16,24,32,40,48,…
6和8的最小公倍数是24。
你知道吗?
我们也可以利用分解质因数的方法,比较简便地求出两个数的最小公倍数。例如:
60 =2×2×3×5
42 =2×3×7
60和42的最小公倍数:
2×3×2×5×7 = 420
60
42
2
30
21
3
10
7
…用公有的质因数2除
…用公有的质因数3除
…除到两个商只有公
因数1为止
60和42的最小公倍数:
2×3×10×7 = 420
为了简便,通常写成右侧的形式。
课堂练习
一个数的倍数的个数是无限的。
3. 2和8的最小公倍数是16。
( )
( )
2. 两个数的公倍数有无限个,最小公倍数的个 数只有1个。
( )
√
√
×
2和8的最小公倍数是8。
1.判断题。
求下列每组数的最小公倍数。
2 和 8 3 和 8 6 和 15 6 和 9
4 和 5 1 和 7 4 和 10 8 和 10
8
24
30
18
20
7
20
40
(2)最小的质数和最小的合数的最大公因数是( ),最小公倍数是( )。
(1)12的倍数有( ),9的倍数有( ),12和9的公倍数有( );最小公倍数是( )。
填一填。
(3)两位数“2□”是2和3的公倍数,□里的数字是( )。这个两位数与16的最大公因数是( ),最小公倍数是( )。
12, 24, 36, 48, 60, 72, 84,…
36, 72, …
36
4
2
9, 18, 27, 36, 45, 54, 63, 72, 81, …
4
8
48
课堂练习
3.选一选。 (将正确答案的序号填在括号里)
(1)连续两个自然数( 0除外)的乘积一定是这两 个数的( ).
A.最大公因数 B.最小公倍数 C.公因数
B
3和5 8和9 12和1 4和15
15
72
12
60
你发现了什么?
互质的两个数,它们的最小公倍数是这两个数的乘积。
找出每组数的最小公倍数。
课堂小结
利用公倍数和最小公倍数可以解决生活中的很多问题,如铺地砖问题、学生排队问题、同一天到达问题等等。
课本练习十七第2题、第5题、第12题。
作业布置
Goodbye~
感谢聆听,下期再会
