五年级下学期数学 4.5.1最小公倍数 课件(20张PPT)
文档属性
| 名称 | 五年级下学期数学 4.5.1最小公倍数 课件(20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 34.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
最小公倍数
学习目标
培养小组合作精神,提高学生对数学的学习兴趣。
通过小组合作探究,教师指导,使学生理解公倍数,最小公倍数的概念。
掌握求两个数最小公倍数的方法,并能正确地求两个数的最小公倍数。
1.找出每组数的最小公倍数。
14和10 6和24 22和33
70
24
66
课堂导入
写一写,说一说。
写出4和5的倍数,再说说一个数倍数的特点。
怎样求一个数的倍数?
4的倍数
5的倍数
一个数倍数的个数是无限的。其中,最小的倍数是它本身,没有最大的倍数。
求一个数的倍数的方法:用这个数分别和1, 2, 3,…相乘,所得的积就是这个数的倍数。
4, 8, 12, 16,
20, 24, …
5, 10, 15, 20,
25, 30, …
新课讲解
你获得了哪些信息?
①用长3dm,宽2dm的长方形墙砖铺正方形。
②使用的墙砖必须都是整块的,不能切割开用半块的。
③求所铺的正方形的边长是多少。
阅读与理解
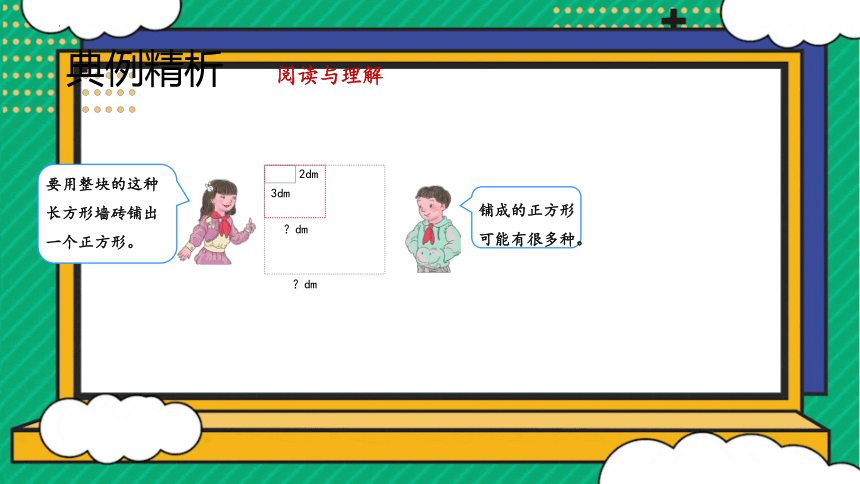
要用整块的这种长方形墙砖铺出一个正方形。
铺成的正方形可能有很多种。
2dm
3dm
?dm
?dm
典例精析
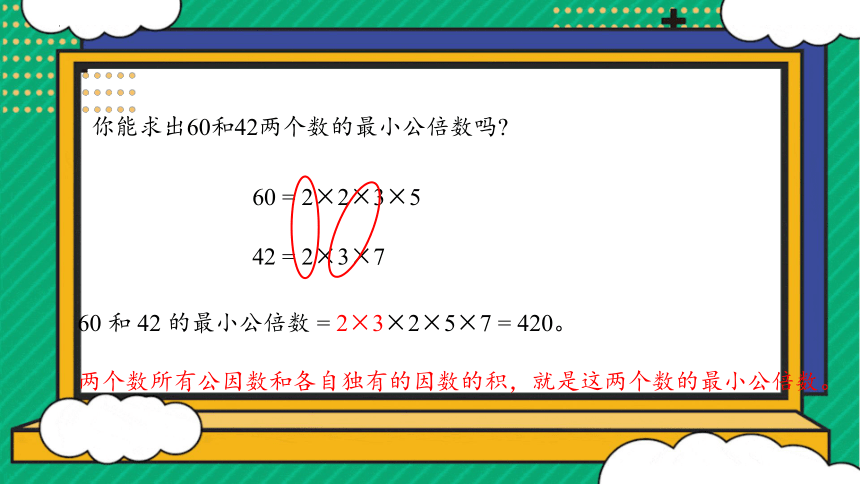
60 = 2×2×3×5
60 和 42 的最小公倍数 = 2×3×2×5×7 = 420。
42 = 2×3×7
两个数所有公因数和各自独有的因数的积,就是这两个数的最小公倍数。
你能求出60和42两个数的最小公倍数吗
方法三
分解质因数法。
(1)方法分析
先分别把6和8分解质因数,再把两个数公有的质因数与各自独有的质因数相乘,可得到这两个数的最小公倍数。
(2)解答过程
6 = 2×3
8 = 2×2×2
2
2
公有的质因数
6和8的最小公倍数是2×3×2×2=24。
(教材第69页例2)
怎样求6和8的公倍数及最小公倍数?
新课讲解
小长方形的个数 正方形的边长
2×3=6个 6分米
4×6=24个 12分米
6×9=54个 18分米
8×12=96个 24分米
用长3分米,宽2分米的墙砖铺正方形
这两路公共汽车同时发车后,过多少分钟两路车第二次同时发车?
6和8的公倍数有24,48,72…最小公倍数是24。
所以,这两路车同时发车后,过24分钟两路车第二次同时发车。
随堂检测
新课讲解
1.找出下列每组数的最小公倍数。你发现了什么?
3和6 2和8 5和6 4和9 3和9 5和10
6 8 30 36 9 10
较大数是较小数的倍数时,这两个数的最
小公倍数是较大数。
两个数的最大公因数是1时,这两个数的最小公数是两个数的乘积。
下面每组数的公倍数中有没有 36 有没有48 有没有 84
6 和 18 21 和 14 12 和 8
36
84
48
课堂练习
做一做
把3和4的倍数、公倍数填在相应的位置,并圈出它们的最小公倍数。
3的倍数
4的倍数
12
24
36
3
…
4
8
3和4的公倍数
(教材第68页“做一做”)
16
20
28
32
…
6
9
15
18
21
27
30
33
39
…
40
新课讲解
想一想,两个数有没有有最大公倍数?
4的倍数
6的倍数
4,
8,
28,
6,
18,
42,
12,
24,
36,
16,
20,
…
32,
40,
36,
…
…
4和6的公倍数
因为一个数的公倍数是无限的,所以两个数的公倍数也是无限的,它们没有最大公倍数,只有最小公倍数。
课堂练习
一种瓷砖长4dm,宽3dm。如果用这种瓷砖铺一个正方形(用的瓷砖必需是整块数),正方形的边长可以是多少分米?最小是多少分米?
正方形的边长可以是12dm,24dm,36dm,…
最小是12dm。
课堂小结
1.几个数公有的倍数,叫做这几个数的公倍数。其中最小的一个叫做它们的最小公倍数。
2.两个数的公倍数的个数是无限的,没有最大的公倍数。
当两个数是倍数关系时,这两个数的最小公倍数就是较大的数;
最小公倍数(2)
两个数所有公因数和各自独有的因数的积,就是这两个数的最小公倍数。
当两个数是互质数时,这两个数的最小公倍数就是这两个数的积。
提升练习
6.(1)按要求填空。
7和35 6和16 12和18 5和13
最大公因数
最小公倍数
最大公因数与最小公倍数的乘积
两个数的乘积
7
35
245
245
2
48
96
96
6
36
216
216
1
65
65
65
同学们再见
最小公倍数
学习目标
培养小组合作精神,提高学生对数学的学习兴趣。
通过小组合作探究,教师指导,使学生理解公倍数,最小公倍数的概念。
掌握求两个数最小公倍数的方法,并能正确地求两个数的最小公倍数。
1.找出每组数的最小公倍数。
14和10 6和24 22和33
70
24
66
课堂导入
写一写,说一说。
写出4和5的倍数,再说说一个数倍数的特点。
怎样求一个数的倍数?
4的倍数
5的倍数
一个数倍数的个数是无限的。其中,最小的倍数是它本身,没有最大的倍数。
求一个数的倍数的方法:用这个数分别和1, 2, 3,…相乘,所得的积就是这个数的倍数。
4, 8, 12, 16,
20, 24, …
5, 10, 15, 20,
25, 30, …
新课讲解
你获得了哪些信息?
①用长3dm,宽2dm的长方形墙砖铺正方形。
②使用的墙砖必须都是整块的,不能切割开用半块的。
③求所铺的正方形的边长是多少。
阅读与理解
要用整块的这种长方形墙砖铺出一个正方形。
铺成的正方形可能有很多种。
2dm
3dm
?dm
?dm
典例精析
60 = 2×2×3×5
60 和 42 的最小公倍数 = 2×3×2×5×7 = 420。
42 = 2×3×7
两个数所有公因数和各自独有的因数的积,就是这两个数的最小公倍数。
你能求出60和42两个数的最小公倍数吗
方法三
分解质因数法。
(1)方法分析
先分别把6和8分解质因数,再把两个数公有的质因数与各自独有的质因数相乘,可得到这两个数的最小公倍数。
(2)解答过程
6 = 2×3
8 = 2×2×2
2
2
公有的质因数
6和8的最小公倍数是2×3×2×2=24。
(教材第69页例2)
怎样求6和8的公倍数及最小公倍数?
新课讲解
小长方形的个数 正方形的边长
2×3=6个 6分米
4×6=24个 12分米
6×9=54个 18分米
8×12=96个 24分米
用长3分米,宽2分米的墙砖铺正方形
这两路公共汽车同时发车后,过多少分钟两路车第二次同时发车?
6和8的公倍数有24,48,72…最小公倍数是24。
所以,这两路车同时发车后,过24分钟两路车第二次同时发车。
随堂检测
新课讲解
1.找出下列每组数的最小公倍数。你发现了什么?
3和6 2和8 5和6 4和9 3和9 5和10
6 8 30 36 9 10
较大数是较小数的倍数时,这两个数的最
小公倍数是较大数。
两个数的最大公因数是1时,这两个数的最小公数是两个数的乘积。
下面每组数的公倍数中有没有 36 有没有48 有没有 84
6 和 18 21 和 14 12 和 8
36
84
48
课堂练习
做一做
把3和4的倍数、公倍数填在相应的位置,并圈出它们的最小公倍数。
3的倍数
4的倍数
12
24
36
3
…
4
8
3和4的公倍数
(教材第68页“做一做”)
16
20
28
32
…
6
9
15
18
21
27
30
33
39
…
40
新课讲解
想一想,两个数有没有有最大公倍数?
4的倍数
6的倍数
4,
8,
28,
6,
18,
42,
12,
24,
36,
16,
20,
…
32,
40,
36,
…
…
4和6的公倍数
因为一个数的公倍数是无限的,所以两个数的公倍数也是无限的,它们没有最大公倍数,只有最小公倍数。
课堂练习
一种瓷砖长4dm,宽3dm。如果用这种瓷砖铺一个正方形(用的瓷砖必需是整块数),正方形的边长可以是多少分米?最小是多少分米?
正方形的边长可以是12dm,24dm,36dm,…
最小是12dm。
课堂小结
1.几个数公有的倍数,叫做这几个数的公倍数。其中最小的一个叫做它们的最小公倍数。
2.两个数的公倍数的个数是无限的,没有最大的公倍数。
当两个数是倍数关系时,这两个数的最小公倍数就是较大的数;
最小公倍数(2)
两个数所有公因数和各自独有的因数的积,就是这两个数的最小公倍数。
当两个数是互质数时,这两个数的最小公倍数就是这两个数的积。
提升练习
6.(1)按要求填空。
7和35 6和16 12和18 5和13
最大公因数
最小公倍数
最大公因数与最小公倍数的乘积
两个数的乘积
7
35
245
245
2
48
96
96
6
36
216
216
1
65
65
65
同学们再见
