1.2动量定理课件(共29张PPT)
文档属性
| 名称 | 1.2动量定理课件(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-05-20 19:54:30 | ||
图片预览







文档简介
(共29张PPT)
1.2 动量定理
第1章 动量守恒定律
问题?
如图所示,跳高比赛时,在运动员落地处为什么要放很厚的海绵垫子
一、动量定理
一个质量为m的物体在光滑的水平面上受到恒力 F 的作用,做匀变速直线运动。在初始时刻,物体的速度为v,经过一段时间Δt,它的速度为v′
右边是物体在Δt这段时间内动量的变化量,左边既与力的大小、方向有关,又与力的作用时间有关。
FΔ t这个物理量反映了力的作用对时间的累积效应
一、动量定理
1.冲量
(1)定义:物理学中把力与力的作用时间的乘积叫做力的冲量.
(2)公式:通常用符号I表示冲量,即 I=Ft.
(3)单位:在国际单位制中,冲量的单位是 N·s.
1 N·s=1 kg·m/s.
(4)矢量:冲量的方向与力的方向一致,冲量的方向跟动量变化量的方向一致。
(4)对冲量的理解
①时间性:冲量不仅与力有关,还与力的作用时间有关,恒力的冲量等于力与力作用时间的乘积,此公式I=Ft只适用于恒力.
②矢量性:对于恒力来说,冲量的方向与力的方向一致;对于作用时间内方向变化的力来说,冲量的方向与相应时间内动量的变化量的方向一致,冲量的运算应用平行四边形定则.
③过程性:冲量是描述力F对时间t的累积效果的物理量,是过程量,必须明确是哪个力在哪段时间内对哪个物体的冲量.
特别提醒:
(1)冲量是矢量,求冲量的大小时一定要注意是力与其对应的时间的乘积。
(2)判断两个力的冲量是否相同,必须满足冲量的大小和方向都相同。
④合力的冲量:
如果是一维情形,可以化为代数和,
如果不在一条直线上,求合冲量遵循平行四边形定则。
两种方法:可分别求每一个力的冲量,再求各冲量的矢量和;如果各个力的作用时间相同,也可以先求合力,再用公式I合=F合Δt求解。
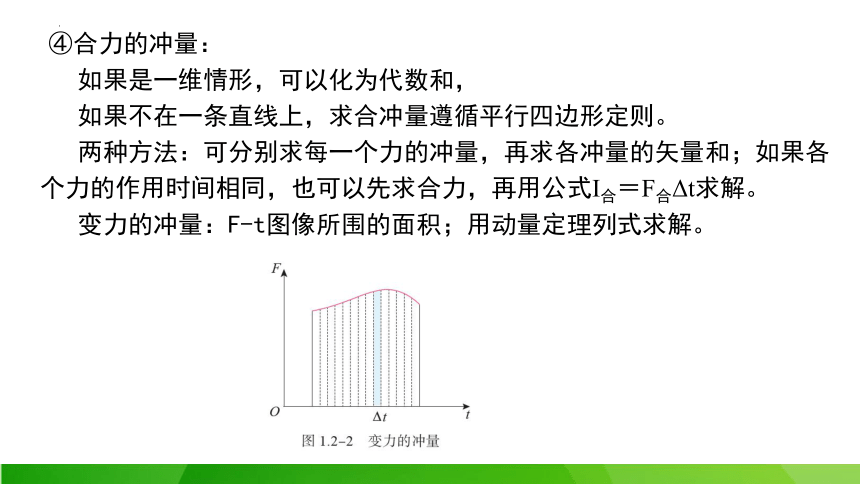
变力的冲量:F-t图像所围的面积;用动量定理列式求解。
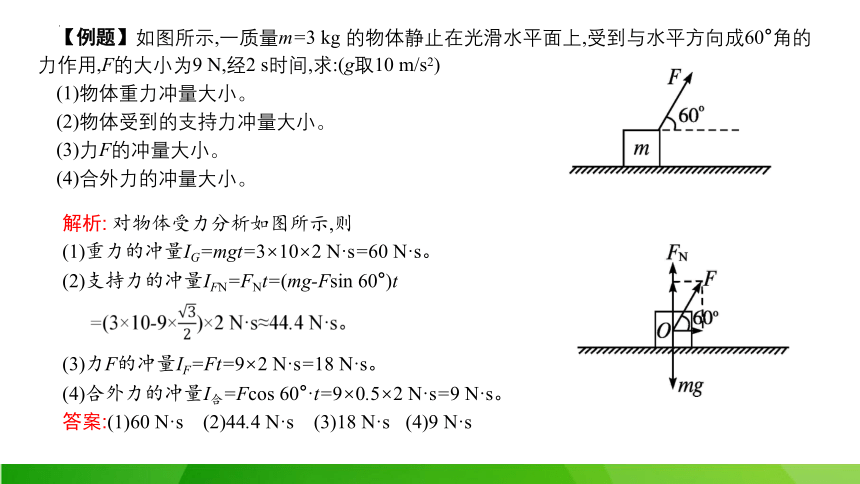
【例题】如图所示,一质量m=3 kg 的物体静止在光滑水平面上,受到与水平方向成60°角的力作用,F的大小为9 N,经2 s时间,求:(g取10 m/s2)
(1)物体重力冲量大小。
(2)物体受到的支持力冲量大小。
(3)力F的冲量大小。
(4)合外力的冲量大小。
解析: 对物体受力分析如图所示,则
(1)重力的冲量IG=mgt=3×10×2 N·s=60 N·s。
(2)支持力的冲量IFN=FNt=(mg-Fsin 60°)t
(3)力F的冲量IF=Ft=9×2 N·s=18 N·s。
(4)合外力的冲量I合=Fcos 60°·t=9×0.5×2 N·s=9 N·s。
答案:(1)60 N·s (2)44.4 N·s (3)18 N·s (4)9 N·s
D
一、动量定理
2.动量定理
(1)内容: 物体在一个过程中所受力的冲量
等于它在这个过程始末的动量变化量
(2)表达式:
I=p′-p 或 F(t′ -t)= mv′-mv
(3)适用对象:动量定理的研究对象通常为单个物体或者可以看作整体的物体系统。
(4)适用范围:宏观物体的低速运动, 微观物体的高速运动。不论是变力还是恒力,不论物体的运动轨迹是直线还是曲线,动量定理都适用。
3.对动量定理的理解
(1) 动量定理反映了合外力的冲量是动量变化的原因。
(2)动量定理的表达式是矢量式,它说明合外力的冲量跟物体动量变化量不仅大小相等,而且方向相同。
运用动量定理主要是一维的问题,要注意规定正方向。
一、动量定理
【例题】质量m=70 kg的撑竿跳高运动员从h=5.0 m高处落到海绵垫上,经Δt1=1 s后停止,则该运动员身体受到的平均冲力约为多少 如果是落到普通沙坑中,经Δt2=0.1 s停下,则沙坑对运动员的平均冲力约为多少 (g取10 m/s2)
解析:以全过程为研究对象,初、末动量的数值都是0,所以运动员的动量变化量为零,根据动量定理,合力的冲量为零,根据自由落体运动的知识,物体下落到地面上所需要的时间是t=1 s
从开始下落到落到海绵垫上停止时,mg(t+Δt1)-FΔt1=0
代入数据,解得F=1 400 N
下落到沙坑中时,mg(t+Δt2)-F'Δt2=0
代入数据,解得F'=7 700 N。
答案:1 400 N 7 700 N
【练习】高空坠物极易对行人造成伤害,若一个50 g 的鸡蛋从一居民楼的25层坠下,与地面的碰撞时间约为2 ms,则该鸡蛋对地面产生的冲击力约为( )
A.10 N B.102N C.103N D.104 N
层楼高约3 m,则h=24×3 m=72 m,设竖直向上为正方向,对鸡蛋冲击地面过程,根据动量定理,有Ft-mgt=0-(-mv),由于冲击时间很短,所以忽略鸡蛋重力的冲量,解得F≈1×103 N,即鸡蛋对地面的冲击力约为103 N,选项C正确。
答案:C
【练习】如图所示,质量为m=2 kg的物体,在水平力F=16 N的作用下,由静止开始沿水平面向右运动.已知物体与水平面间的动摩擦因数μ=0.2.若F作用t1=2 s后撤去,撤去F后又经t2=2s物体与竖直墙壁相碰,若物体与墙壁作用时间t3=0.1 s,碰撞后反向弹回的速度v′=6 m/s,求墙壁对物体的平均作用力.(g取10 m/s2)
4、应用动量定理定量计算的一般步骤:
①选定研究对象,明确运动过程。
②进行受力分析和运动的初、末状态分析。
③选定正方向,根据动量定理列方程求解。
应用动量定理解题时首先对物体受力分析,明确各个分力和合力是正确应用动量定理的前提。
一、动量定理
3、动量定理的应用:
(1)定性分析有关现象:
①物体的动量变化量一定时,力的作用时间越短,力就越大;力的作用时间越长,力就越小。
②作用力一定时,力的作用时间越长,动量变化量越大;力的作用时间越短,动量变化量越小。
(2)定量计算。
①应用动量定理可以计算某力或合力的冲量,也可用于计算变力的冲量。
②应用动量定理可以计算某一过程中的平均作用力,通常多用于计算持续作用的变力的平均大小。
③应用动量定理计算物体的初、末动量,尤其方便处理物体受瞬间冲量的问题。
一、动量定理
【例题】从同样高度落下的玻璃杯,掉在水泥地上容易打碎,而掉在草地上不容易打碎,其原因是( )
A.掉在水泥地上的玻璃杯动量大,而掉在草地上的玻璃杯动量小
B.掉在水泥地上的玻璃杯动量改变大,掉在草地上的玻璃杯动量改变小
C.掉在水泥地上的玻璃杯动量改变快,掉在草地上的玻璃杯动量改变慢
D.掉在水泥地上的玻璃杯与地面接触时,相互作用时间短,而掉在草地上的玻璃杯与地面接触时作用时间长
【例题】 在撑竿跳高场地落地点铺有厚厚垫子的目的是减少运动员受伤,理由是( )
A.减小冲量,起到安全作用
B.减小动量变化量,起到安全作用
C.垫子的反弹作用使人安全
D.减小动量变化率,起到安全作用
解析:跳高运动员在落地的过程中,动量变化一定,由动量定理可知,运动员受到的冲量I一定,跳高运动员在跳高时跳到沙坑里或跳到海绵垫上可以延长着地过程的作用时间t,由I=Ft可知,延长时间t可以减小运动员所受到的平均冲力F,即减小动量变化率,起到安全作用,故D正确,ABC错误。
答案:D
【练习】1998年6月18日,清华大学对富康轿车成功地进行了中国轿车史上的第一次碰撞安全性实验,成为“中华第一撞”,从此,我国汽车整体安全性碰撞实验开始与国际接轨,在碰撞过程中,关于安全气囊的保护作用认识正确的 ( )
A.安全气囊的作用减小了驾驶员的动量变化
B.安全气囊减小了驾驶员受到撞击力的冲量
C.安全气囊主要是减小了驾驶员的动量变化率
D.安全气囊延长了撞击力的作用时间,从而使得动量
变化更大
解析:在碰撞过程中,人的动量的变化量是一定的,而用安全气囊后增加了作用的时间,根据动量定理Ft=ΔP可知,可以减小驾驶员受到的冲击力,即是减小了驾驶员的动量变化率,故选C。
【思考】 杂技表演时,常可看见有人用铁锤猛击放在“大力士”身上的条石,石裂而人不伤,试分析其中道理.
【思考】做一做:将纸条的一端压在钢笔帽下,如图a,用手慢慢拉动纸条,会看到什么现象 如图b,拉紧纸条,用手向下快速击打纸条,会看到什么现象 并解释原因。
要点提示:图a,用手慢慢拉动纸条,可以看到钢笔帽跟着纸带移动起来。图b,拉紧纸条,用手向下快速击打纸条,纸条从钢笔帽下抽出,钢笔帽静止不动。
物体动量的改变取决于外力的冲量大小,钢笔帽在水平方向受到纸条的摩擦力,第一次作用时间长,动量变化大,钢笔帽动;第二次作用时间短,冲量小,动量变化小,钢笔帽不动。
总结:
应用动量定理的四点注意事项
(1)明确物体受到冲量作用的结果是导致物体动量的变化。冲量和动量都是矢量,它们的加、减运算都遵循平行四边形定则。
(2)列方程前首先要选取正方向,与规定的正方向一致的力或动量取正值,反之取负值,而不能只关注力或动量数值的大小。
(3)分析速度时一定要选取同一个参考系,未加说明时一般是选地面为参考系,同一道题目中一般不要选取不同的参考系。
(4)公式中的冲量应是合外力的冲量,求动量的变化量时要严格按公式,且要注意是末动量减去初动量。
【例题】一枚竖直向上发射的火箭,除燃料外质量m火箭=6000 kg,火箭喷气的速度为1000 m/s,在开始时每秒大约要喷出多少质量的气体才能支持火箭的重力?如果要使火箭开始时有19.6 m/s2向上的加速度,则每秒要喷出多少气体?
【例题】质量为1 kg的物体做直线运动,其速度图象如图所示。则物体在前10 s内和后10 s内所受合力的冲量分别是( )
A.10 N·s,10 N·s B.10 N·s,-10 N·s
C.0,10 N·s D.0,-10 N·s
解析:根据动量定理,物体所受合力的冲量
等于其动量的变化量。故0~10 s内,v1=5 m/s,v2=5 m/s,
则Δp1=0,所以I1=0;
10~20 s内,v1=5 m/s,v2=-5 m/s,
故Δp2=mv2-mv1=[1×(-5)-1×5] kg·m/s=-10 kg·m/s=-10 N·s,选项D正确。
答案:D
【例5】 最大截面S=5 m2的一艘宇宙飞船,以速度v=10 km/s在太空中航行时,进入静止的、密度ρ=2×10-5 kg/m3的微陨石云中.如果微陨石与飞船相撞时都附着在飞船上,要使飞船维持原速度前进,飞船的推力应为多大?
1.在Δt时间内,附着在飞船上的微陨石质量Δm是多少,应如何求Δm
2.在Δt时间内,落到飞船上的微陨石动量增加了多少?
【练习】高压采煤水枪出水口的截面积为S,水的射速为v,射到煤层上后,水速度为零,若水的密度为ρ,求水对煤层的冲力.
解析:我们取一小段时间内射到煤层上的水进行研究(下图),这部分水在较短时间内速度变为零,煤一定对水产生力的作用.因此,可以由动量定理来求煤对水的平均作用力,再由牛顿第三定律就知道水对煤的作用力.
设在Δt时间内射出的水的质量为Δm,则Δm=ρSvΔt,以Δm为研究对象,它在Δt内动量变化为Δp=Δm(0-v)=-ρSv2Δt.
设F为水对煤层的冲力,F′为煤层对水的反冲力,以F′的方向为正方向.根据动量定理(忽略水的重力)有F′Δt=-ρSv2Δt,所以F′=-ρSv2.
根据牛顿第三定律得F=-F′=ρSv2.
总结:
微元法是物理学上用来处理变质量问题时常用的思想方法.在本章中对这类有连续质量流动的问题,在应用动量定理时关键在于研究对象的选取,通常所采用的方法是选Δt时间内发生相互作用的流体为研究对象,确定发生相互作用前后的动量.然后由动量定理解题.
本节到此结束,谢谢!
1.2 动量定理
第1章 动量守恒定律
问题?
如图所示,跳高比赛时,在运动员落地处为什么要放很厚的海绵垫子
一、动量定理
一个质量为m的物体在光滑的水平面上受到恒力 F 的作用,做匀变速直线运动。在初始时刻,物体的速度为v,经过一段时间Δt,它的速度为v′
右边是物体在Δt这段时间内动量的变化量,左边既与力的大小、方向有关,又与力的作用时间有关。
FΔ t这个物理量反映了力的作用对时间的累积效应
一、动量定理
1.冲量
(1)定义:物理学中把力与力的作用时间的乘积叫做力的冲量.
(2)公式:通常用符号I表示冲量,即 I=Ft.
(3)单位:在国际单位制中,冲量的单位是 N·s.
1 N·s=1 kg·m/s.
(4)矢量:冲量的方向与力的方向一致,冲量的方向跟动量变化量的方向一致。
(4)对冲量的理解
①时间性:冲量不仅与力有关,还与力的作用时间有关,恒力的冲量等于力与力作用时间的乘积,此公式I=Ft只适用于恒力.
②矢量性:对于恒力来说,冲量的方向与力的方向一致;对于作用时间内方向变化的力来说,冲量的方向与相应时间内动量的变化量的方向一致,冲量的运算应用平行四边形定则.
③过程性:冲量是描述力F对时间t的累积效果的物理量,是过程量,必须明确是哪个力在哪段时间内对哪个物体的冲量.
特别提醒:
(1)冲量是矢量,求冲量的大小时一定要注意是力与其对应的时间的乘积。
(2)判断两个力的冲量是否相同,必须满足冲量的大小和方向都相同。
④合力的冲量:
如果是一维情形,可以化为代数和,
如果不在一条直线上,求合冲量遵循平行四边形定则。
两种方法:可分别求每一个力的冲量,再求各冲量的矢量和;如果各个力的作用时间相同,也可以先求合力,再用公式I合=F合Δt求解。
变力的冲量:F-t图像所围的面积;用动量定理列式求解。
【例题】如图所示,一质量m=3 kg 的物体静止在光滑水平面上,受到与水平方向成60°角的力作用,F的大小为9 N,经2 s时间,求:(g取10 m/s2)
(1)物体重力冲量大小。
(2)物体受到的支持力冲量大小。
(3)力F的冲量大小。
(4)合外力的冲量大小。
解析: 对物体受力分析如图所示,则
(1)重力的冲量IG=mgt=3×10×2 N·s=60 N·s。
(2)支持力的冲量IFN=FNt=(mg-Fsin 60°)t
(3)力F的冲量IF=Ft=9×2 N·s=18 N·s。
(4)合外力的冲量I合=Fcos 60°·t=9×0.5×2 N·s=9 N·s。
答案:(1)60 N·s (2)44.4 N·s (3)18 N·s (4)9 N·s
D
一、动量定理
2.动量定理
(1)内容: 物体在一个过程中所受力的冲量
等于它在这个过程始末的动量变化量
(2)表达式:
I=p′-p 或 F(t′ -t)= mv′-mv
(3)适用对象:动量定理的研究对象通常为单个物体或者可以看作整体的物体系统。
(4)适用范围:宏观物体的低速运动, 微观物体的高速运动。不论是变力还是恒力,不论物体的运动轨迹是直线还是曲线,动量定理都适用。
3.对动量定理的理解
(1) 动量定理反映了合外力的冲量是动量变化的原因。
(2)动量定理的表达式是矢量式,它说明合外力的冲量跟物体动量变化量不仅大小相等,而且方向相同。
运用动量定理主要是一维的问题,要注意规定正方向。
一、动量定理
【例题】质量m=70 kg的撑竿跳高运动员从h=5.0 m高处落到海绵垫上,经Δt1=1 s后停止,则该运动员身体受到的平均冲力约为多少 如果是落到普通沙坑中,经Δt2=0.1 s停下,则沙坑对运动员的平均冲力约为多少 (g取10 m/s2)
解析:以全过程为研究对象,初、末动量的数值都是0,所以运动员的动量变化量为零,根据动量定理,合力的冲量为零,根据自由落体运动的知识,物体下落到地面上所需要的时间是t=1 s
从开始下落到落到海绵垫上停止时,mg(t+Δt1)-FΔt1=0
代入数据,解得F=1 400 N
下落到沙坑中时,mg(t+Δt2)-F'Δt2=0
代入数据,解得F'=7 700 N。
答案:1 400 N 7 700 N
【练习】高空坠物极易对行人造成伤害,若一个50 g 的鸡蛋从一居民楼的25层坠下,与地面的碰撞时间约为2 ms,则该鸡蛋对地面产生的冲击力约为( )
A.10 N B.102N C.103N D.104 N
层楼高约3 m,则h=24×3 m=72 m,设竖直向上为正方向,对鸡蛋冲击地面过程,根据动量定理,有Ft-mgt=0-(-mv),由于冲击时间很短,所以忽略鸡蛋重力的冲量,解得F≈1×103 N,即鸡蛋对地面的冲击力约为103 N,选项C正确。
答案:C
【练习】如图所示,质量为m=2 kg的物体,在水平力F=16 N的作用下,由静止开始沿水平面向右运动.已知物体与水平面间的动摩擦因数μ=0.2.若F作用t1=2 s后撤去,撤去F后又经t2=2s物体与竖直墙壁相碰,若物体与墙壁作用时间t3=0.1 s,碰撞后反向弹回的速度v′=6 m/s,求墙壁对物体的平均作用力.(g取10 m/s2)
4、应用动量定理定量计算的一般步骤:
①选定研究对象,明确运动过程。
②进行受力分析和运动的初、末状态分析。
③选定正方向,根据动量定理列方程求解。
应用动量定理解题时首先对物体受力分析,明确各个分力和合力是正确应用动量定理的前提。
一、动量定理
3、动量定理的应用:
(1)定性分析有关现象:
①物体的动量变化量一定时,力的作用时间越短,力就越大;力的作用时间越长,力就越小。
②作用力一定时,力的作用时间越长,动量变化量越大;力的作用时间越短,动量变化量越小。
(2)定量计算。
①应用动量定理可以计算某力或合力的冲量,也可用于计算变力的冲量。
②应用动量定理可以计算某一过程中的平均作用力,通常多用于计算持续作用的变力的平均大小。
③应用动量定理计算物体的初、末动量,尤其方便处理物体受瞬间冲量的问题。
一、动量定理
【例题】从同样高度落下的玻璃杯,掉在水泥地上容易打碎,而掉在草地上不容易打碎,其原因是( )
A.掉在水泥地上的玻璃杯动量大,而掉在草地上的玻璃杯动量小
B.掉在水泥地上的玻璃杯动量改变大,掉在草地上的玻璃杯动量改变小
C.掉在水泥地上的玻璃杯动量改变快,掉在草地上的玻璃杯动量改变慢
D.掉在水泥地上的玻璃杯与地面接触时,相互作用时间短,而掉在草地上的玻璃杯与地面接触时作用时间长
【例题】 在撑竿跳高场地落地点铺有厚厚垫子的目的是减少运动员受伤,理由是( )
A.减小冲量,起到安全作用
B.减小动量变化量,起到安全作用
C.垫子的反弹作用使人安全
D.减小动量变化率,起到安全作用
解析:跳高运动员在落地的过程中,动量变化一定,由动量定理可知,运动员受到的冲量I一定,跳高运动员在跳高时跳到沙坑里或跳到海绵垫上可以延长着地过程的作用时间t,由I=Ft可知,延长时间t可以减小运动员所受到的平均冲力F,即减小动量变化率,起到安全作用,故D正确,ABC错误。
答案:D
【练习】1998年6月18日,清华大学对富康轿车成功地进行了中国轿车史上的第一次碰撞安全性实验,成为“中华第一撞”,从此,我国汽车整体安全性碰撞实验开始与国际接轨,在碰撞过程中,关于安全气囊的保护作用认识正确的 ( )
A.安全气囊的作用减小了驾驶员的动量变化
B.安全气囊减小了驾驶员受到撞击力的冲量
C.安全气囊主要是减小了驾驶员的动量变化率
D.安全气囊延长了撞击力的作用时间,从而使得动量
变化更大
解析:在碰撞过程中,人的动量的变化量是一定的,而用安全气囊后增加了作用的时间,根据动量定理Ft=ΔP可知,可以减小驾驶员受到的冲击力,即是减小了驾驶员的动量变化率,故选C。
【思考】 杂技表演时,常可看见有人用铁锤猛击放在“大力士”身上的条石,石裂而人不伤,试分析其中道理.
【思考】做一做:将纸条的一端压在钢笔帽下,如图a,用手慢慢拉动纸条,会看到什么现象 如图b,拉紧纸条,用手向下快速击打纸条,会看到什么现象 并解释原因。
要点提示:图a,用手慢慢拉动纸条,可以看到钢笔帽跟着纸带移动起来。图b,拉紧纸条,用手向下快速击打纸条,纸条从钢笔帽下抽出,钢笔帽静止不动。
物体动量的改变取决于外力的冲量大小,钢笔帽在水平方向受到纸条的摩擦力,第一次作用时间长,动量变化大,钢笔帽动;第二次作用时间短,冲量小,动量变化小,钢笔帽不动。
总结:
应用动量定理的四点注意事项
(1)明确物体受到冲量作用的结果是导致物体动量的变化。冲量和动量都是矢量,它们的加、减运算都遵循平行四边形定则。
(2)列方程前首先要选取正方向,与规定的正方向一致的力或动量取正值,反之取负值,而不能只关注力或动量数值的大小。
(3)分析速度时一定要选取同一个参考系,未加说明时一般是选地面为参考系,同一道题目中一般不要选取不同的参考系。
(4)公式中的冲量应是合外力的冲量,求动量的变化量时要严格按公式,且要注意是末动量减去初动量。
【例题】一枚竖直向上发射的火箭,除燃料外质量m火箭=6000 kg,火箭喷气的速度为1000 m/s,在开始时每秒大约要喷出多少质量的气体才能支持火箭的重力?如果要使火箭开始时有19.6 m/s2向上的加速度,则每秒要喷出多少气体?
【例题】质量为1 kg的物体做直线运动,其速度图象如图所示。则物体在前10 s内和后10 s内所受合力的冲量分别是( )
A.10 N·s,10 N·s B.10 N·s,-10 N·s
C.0,10 N·s D.0,-10 N·s
解析:根据动量定理,物体所受合力的冲量
等于其动量的变化量。故0~10 s内,v1=5 m/s,v2=5 m/s,
则Δp1=0,所以I1=0;
10~20 s内,v1=5 m/s,v2=-5 m/s,
故Δp2=mv2-mv1=[1×(-5)-1×5] kg·m/s=-10 kg·m/s=-10 N·s,选项D正确。
答案:D
【例5】 最大截面S=5 m2的一艘宇宙飞船,以速度v=10 km/s在太空中航行时,进入静止的、密度ρ=2×10-5 kg/m3的微陨石云中.如果微陨石与飞船相撞时都附着在飞船上,要使飞船维持原速度前进,飞船的推力应为多大?
1.在Δt时间内,附着在飞船上的微陨石质量Δm是多少,应如何求Δm
2.在Δt时间内,落到飞船上的微陨石动量增加了多少?
【练习】高压采煤水枪出水口的截面积为S,水的射速为v,射到煤层上后,水速度为零,若水的密度为ρ,求水对煤层的冲力.
解析:我们取一小段时间内射到煤层上的水进行研究(下图),这部分水在较短时间内速度变为零,煤一定对水产生力的作用.因此,可以由动量定理来求煤对水的平均作用力,再由牛顿第三定律就知道水对煤的作用力.
设在Δt时间内射出的水的质量为Δm,则Δm=ρSvΔt,以Δm为研究对象,它在Δt内动量变化为Δp=Δm(0-v)=-ρSv2Δt.
设F为水对煤层的冲力,F′为煤层对水的反冲力,以F′的方向为正方向.根据动量定理(忽略水的重力)有F′Δt=-ρSv2Δt,所以F′=-ρSv2.
根据牛顿第三定律得F=-F′=ρSv2.
总结:
微元法是物理学上用来处理变质量问题时常用的思想方法.在本章中对这类有连续质量流动的问题,在应用动量定理时关键在于研究对象的选取,通常所采用的方法是选Δt时间内发生相互作用的流体为研究对象,确定发生相互作用前后的动量.然后由动量定理解题.
本节到此结束,谢谢!
