8.6.3 平面与平面垂直的性质课件-2021-2022学年高一下学期数学人教A版(2019)必修第二册(共15张PPT)
文档属性
| 名称 | 8.6.3 平面与平面垂直的性质课件-2021-2022学年高一下学期数学人教A版(2019)必修第二册(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 600.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 21:26:35 | ||
图片预览

文档简介
(共15张PPT)
8.6.3 平面与平面垂直的性质
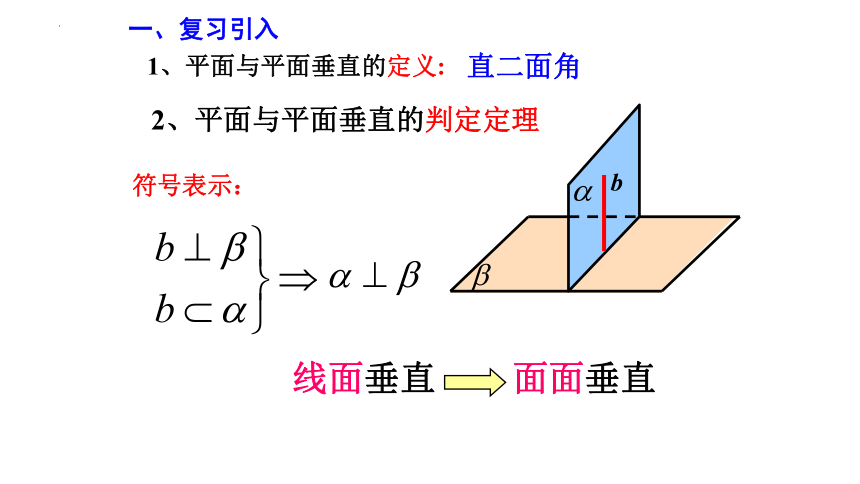
1、平面与平面垂直的定义:
2、平面与平面垂直的判定定理
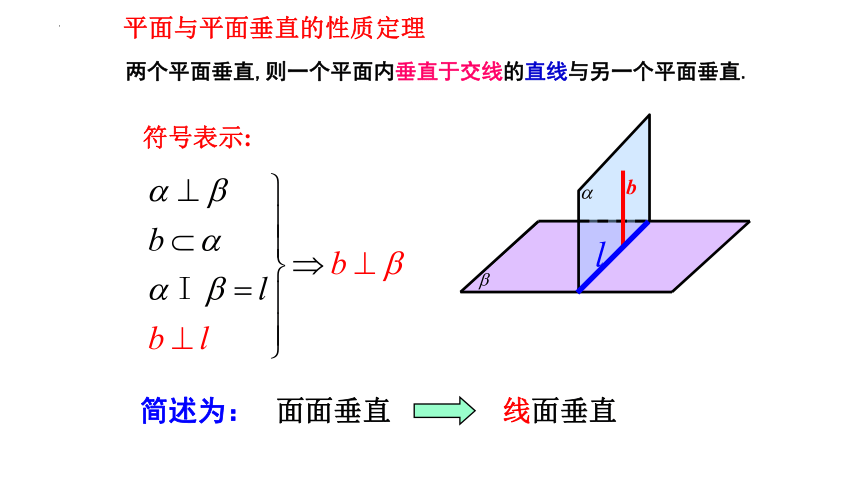
b
直二面角
面面垂直
线面垂直
一、复习引入
符号表示:
α
β
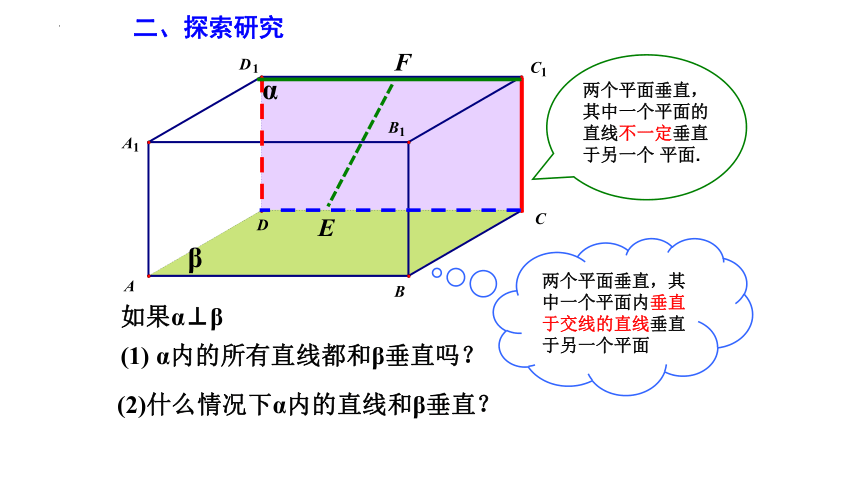
如果α⊥β
(1) α内的所有直线都和β垂直吗?
E
F
(2)什么情况下α内的直线和β垂直?
两个平面垂直,其中一个平面的直线不一定垂直于另一个 平面.
两个平面垂直,其中一个平面内垂直于交线的直线垂直于另一个平面
二、探索研究
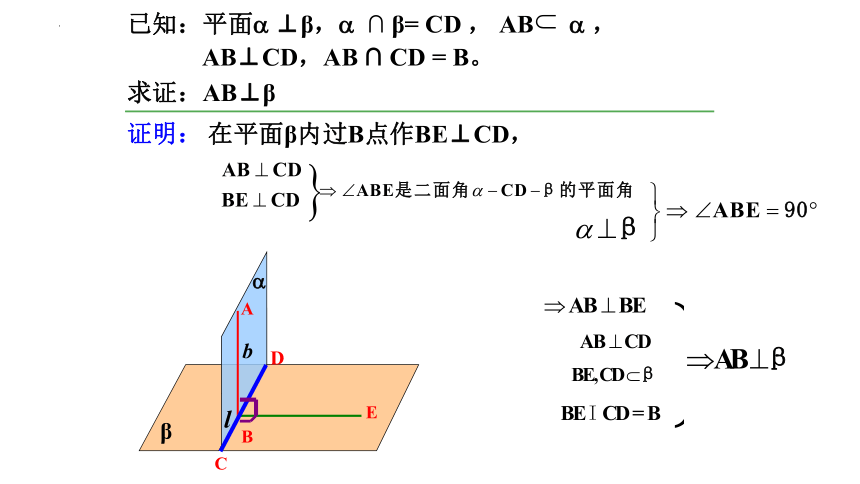
已知:平面 ⊥β, ∩ β= CD , AB ,
求证:AB⊥β
证明:
在平面β内过B点作BE⊥CD,
AB⊥CD,AB ∩ CD = B。
β
A
B
C
D
E
b
l
b
简述为:
面面垂直
线面垂直
符号表示:
平面与平面垂直的性质定理
两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.
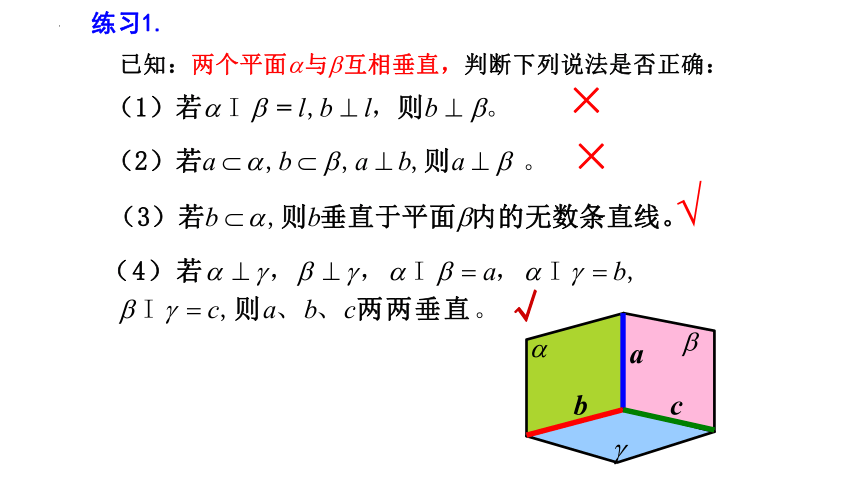
√
×
×
√
a
b
c
练习1.
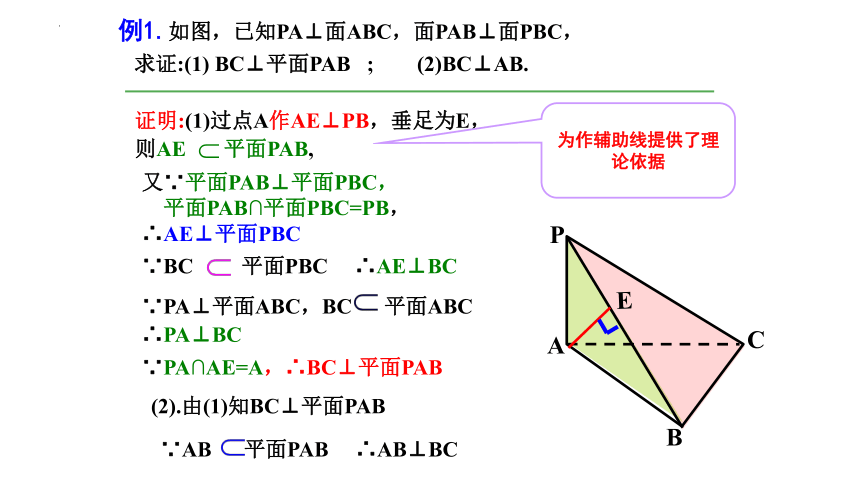
例1.如图,已知PA⊥面ABC,面PAB⊥面PBC,
求证:(1) BC⊥平面PAB ; (2)BC⊥AB.
P
A
B
C
E
∵PA⊥平面ABC,BC 平面ABC
∴PA⊥BC
∵PA∩AE=A,∴BC⊥平面PAB
证明:(1)过点A作AE⊥PB,垂足为E,则AE 平面PAB,
又∵平面PAB⊥平面PBC,
平面PAB∩平面PBC=PB,
∴AE⊥平面PBC
∵BC 平面PBC ∴AE⊥BC
∵AB 平面PAB ∴AB⊥BC
(2).由(1)知BC⊥平面PAB
为作辅助线提供了理论依据
如图所示,在四棱锥P-ABCD中,底面ABCD是边长为a的菱形,且∠DAB=60°,
侧面PAD为正三角形,其所在的平面垂直于底面ABCD,G为AD的中点. (1)求证:BG⊥平面PAD; (2)求证:AD⊥PB.
练习2.
证题思路:
线线垂直 线面垂直
面面垂直 线面垂直
如图所示,在四棱锥P-ABCD中,底面ABCD是边长为a的菱形,且∠DAB=60°,
侧面PAD为正三角形,其所在的平面垂直于底面ABCD,G为AD的中点. (1)求证:BG⊥平面PAD; (2)求证:AD⊥PB.
练习2.
证明:(1)如图所示,连接BD.
∵ 菱形ABCD中,∠DAB=60°,
∴ △ABD为正三角形.
∵ G为AD的中点,
∴BG⊥AD.
∵平面PAD⊥平面ABCD,BG 平面ABCD,平面PAD∩平面ABCD=AD,
∴ BG⊥平面PAD.
(2)如图所示,连接PG.
∵△PAD为正三角形,G为AD的中点,∴PG⊥AD.由(1)知BG⊥AD,PG∩BG=G,BG 平面PBG,PG 平面PBG,
∴ AD⊥平面PGB.
∵ PB 平面PGB,
∴ AD⊥PB.
1、平面与平面垂直的性质定理 :两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
2、证明线面垂直的方法:
线线垂直→线面垂直;面面垂直→线面垂直.
3、线线、线面、面面之间的关系的转化是解决空间图形问题的重要思想方法。
为作辅助线提供了理论依据
三、小结反思
B
P
A
C
O
如图,AB是⊙O的直径,C是圆周上不同于A,B的任意一点,平面PAC⊥平面ABC,
试判断BC与平面PAC的位置关系,并证明。
作业:
课后思考:
如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,
∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,
构成几何体A BCD,则在几何体A BCD中,下列结论正确的是( )
A.平面ABD⊥平面ABC B.平面ADC⊥平面BDC
C.平面ABC⊥平面BDC D.平面ADC⊥平面ABC
解析:由已知得BA⊥AD,CD⊥BD ,
∵平面ABD⊥平面BCD,
∴ CD⊥平面ABD,
∴ CD⊥AB,
∴ AB⊥平面ADC.
又∵ AB 平面ABC,
∴平面ABC⊥平面ADC.
答案:D
如图,以正方形ABCD的对角线AC为折痕,使△ADC和△ABC折成相垂直的两个面,求BD与平面ABC所成的角。
A
B
C
D
D
A
B
C
O
O
折成
课后思考
8.6.3 平面与平面垂直的性质
1、平面与平面垂直的定义:
2、平面与平面垂直的判定定理
b
直二面角
面面垂直
线面垂直
一、复习引入
符号表示:
α
β
如果α⊥β
(1) α内的所有直线都和β垂直吗?
E
F
(2)什么情况下α内的直线和β垂直?
两个平面垂直,其中一个平面的直线不一定垂直于另一个 平面.
两个平面垂直,其中一个平面内垂直于交线的直线垂直于另一个平面
二、探索研究
已知:平面 ⊥β, ∩ β= CD , AB ,
求证:AB⊥β
证明:
在平面β内过B点作BE⊥CD,
AB⊥CD,AB ∩ CD = B。
β
A
B
C
D
E
b
l
b
简述为:
面面垂直
线面垂直
符号表示:
平面与平面垂直的性质定理
两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.
√
×
×
√
a
b
c
练习1.
例1.如图,已知PA⊥面ABC,面PAB⊥面PBC,
求证:(1) BC⊥平面PAB ; (2)BC⊥AB.
P
A
B
C
E
∵PA⊥平面ABC,BC 平面ABC
∴PA⊥BC
∵PA∩AE=A,∴BC⊥平面PAB
证明:(1)过点A作AE⊥PB,垂足为E,则AE 平面PAB,
又∵平面PAB⊥平面PBC,
平面PAB∩平面PBC=PB,
∴AE⊥平面PBC
∵BC 平面PBC ∴AE⊥BC
∵AB 平面PAB ∴AB⊥BC
(2).由(1)知BC⊥平面PAB
为作辅助线提供了理论依据
如图所示,在四棱锥P-ABCD中,底面ABCD是边长为a的菱形,且∠DAB=60°,
侧面PAD为正三角形,其所在的平面垂直于底面ABCD,G为AD的中点. (1)求证:BG⊥平面PAD; (2)求证:AD⊥PB.
练习2.
证题思路:
线线垂直 线面垂直
面面垂直 线面垂直
如图所示,在四棱锥P-ABCD中,底面ABCD是边长为a的菱形,且∠DAB=60°,
侧面PAD为正三角形,其所在的平面垂直于底面ABCD,G为AD的中点. (1)求证:BG⊥平面PAD; (2)求证:AD⊥PB.
练习2.
证明:(1)如图所示,连接BD.
∵ 菱形ABCD中,∠DAB=60°,
∴ △ABD为正三角形.
∵ G为AD的中点,
∴BG⊥AD.
∵平面PAD⊥平面ABCD,BG 平面ABCD,平面PAD∩平面ABCD=AD,
∴ BG⊥平面PAD.
(2)如图所示,连接PG.
∵△PAD为正三角形,G为AD的中点,∴PG⊥AD.由(1)知BG⊥AD,PG∩BG=G,BG 平面PBG,PG 平面PBG,
∴ AD⊥平面PGB.
∵ PB 平面PGB,
∴ AD⊥PB.
1、平面与平面垂直的性质定理 :两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
2、证明线面垂直的方法:
线线垂直→线面垂直;面面垂直→线面垂直.
3、线线、线面、面面之间的关系的转化是解决空间图形问题的重要思想方法。
为作辅助线提供了理论依据
三、小结反思
B
P
A
C
O
如图,AB是⊙O的直径,C是圆周上不同于A,B的任意一点,平面PAC⊥平面ABC,
试判断BC与平面PAC的位置关系,并证明。
作业:
课后思考:
如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,
∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,
构成几何体A BCD,则在几何体A BCD中,下列结论正确的是( )
A.平面ABD⊥平面ABC B.平面ADC⊥平面BDC
C.平面ABC⊥平面BDC D.平面ADC⊥平面ABC
解析:由已知得BA⊥AD,CD⊥BD ,
∵平面ABD⊥平面BCD,
∴ CD⊥平面ABD,
∴ CD⊥AB,
∴ AB⊥平面ADC.
又∵ AB 平面ABC,
∴平面ABC⊥平面ADC.
答案:D
如图,以正方形ABCD的对角线AC为折痕,使△ADC和△ABC折成相垂直的两个面,求BD与平面ABC所成的角。
A
B
C
D
D
A
B
C
O
O
折成
课后思考
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
