湘教版九年级上册3.2 平行线分线段成比例课件(共20张PPT)
文档属性
| 名称 | 湘教版九年级上册3.2 平行线分线段成比例课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 755.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 16:19:07 | ||
图片预览






文档简介
(共20张PPT)
第3章 图形的相似
3.2 平行线分线段成比例
在四条线段中, 如果其中两条线段的比等于另外两条线段的比, 那么这四条线段叫作成比例线段, 简称为比例线段.
平行四边形、矩形、正方形、菱形中的四条线段分别是成比例线段.
知识回顾
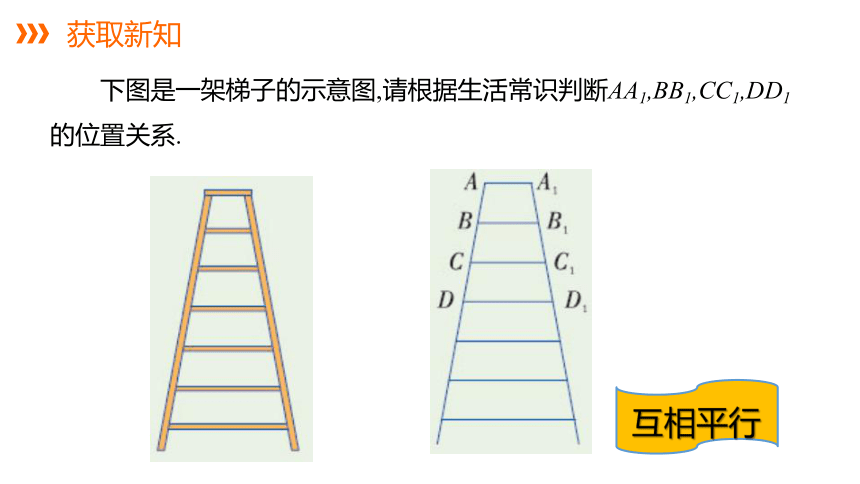
互相平行
下图是一架梯子的示意图,请根据生活常识判断AA1,BB1,CC1,DD1的位置关系.
获取新知
a
b
c
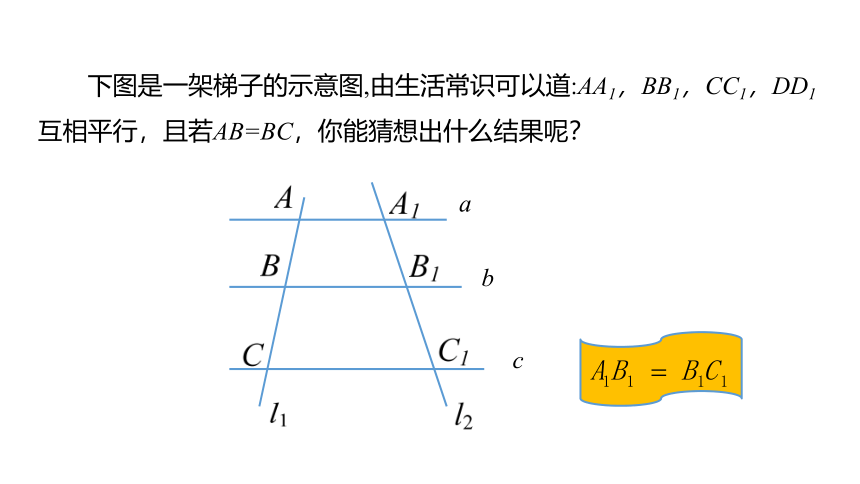
下图是一架梯子的示意图,由生活常识可以道:AA1,BB1,CC1,DD1互相平行,且若AB=BC,你能猜想出什么结果呢?
a
b
c
如图,已知直线a∥b∥c.直线l1,l2被直线a,b,c截得的线段分别为AB,BC和A1B1,B1C1,且AB=BC,要证明A1B1=B1C1,能不做辅助线证明吗?如果必须做辅助线,你考虑怎么做呢?
由于a//b//c,l3//l2,因此由“夹在两平行线间的平行线段相等”可知A2B=A1B1,BC2=B1C1.
a
b
c
过点B作直线l3//l2,分别与直线a,c相交于点A2,C2,
在△BAA2和△BCC2中:
∠ABA2=∠CBC2,BA=BC,∠BAA2=∠BCC2,
因此△BAA2≌△BCC2,从而BA2=BC2,
所以A1B1=B1C1.
两条直线被一组平行线所截,如果在其中一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.
归纳总结
a
b
c
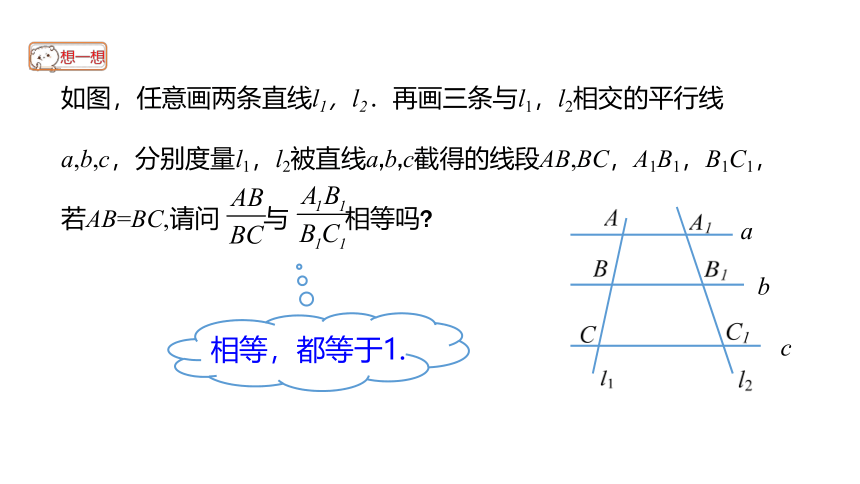
相等,都等于1.
如图,任意画两条直线l1,l2.再画三条与l1,l2相交的平行线a,b,c,分别度量l1,l2被直线a,b,c截得的线段AB,BC,A1B1,B1C1,若AB=BC,请问 与 相等吗
平移直线c,若 ,请问 与 还相等吗
证明: ,则把线段AB二等分,分点为D.
过点D作直线d∥a,交l2于点D1.如图:
把线段BC三等分,三等分点为E,F,分别过点E,F作直线e∥a,f∥a,分别交l2于点E1,F1.
e
a
b
c
f
d
e
a
b
c
f
d
若条件“ ”改为“ ”(其中m,n是正整数),请问 的结果是什么呢?
a
b
c
两条直线被一组平行线所截,所得的对应线段成比例.
我们把以上基本事实简称为平行线分线段成比例.
归纳总结
平行于三角形一边的直线截其他两边所得的对应线段成比例.
归纳总结
例 如图,已AA1//BB1//CC1,AB=2,BC=3,A1B1=1.5, 求B1C1的长.
例题讲解
解:由平行线段成比例可知,
,即 ,
因此,
1.如图,AC,BD相交于点O,直线MN过点O,且BA//MN//CD,已知OA=3,OB=1,OD=2,求OC的长.
解:
∵ BA//MN//CD,
∴ ,
∵ OA=3,OB=1,OD=2,
∴ ,
∴ OC=6.
随堂演练
2.如图,点D,E分别在△ABC的边AB,AC上,且DE∥BC,若AB=3,AD=2,EC=1.8,求AC的长.
解:∵ DE//BC,
∴ ,
∵ AB=3,AD=2,
∴ DB=1,
∴ ,
∴ AE=3.6,
∴ AC=3.6+1.8=5.4.
课堂小结
两条直线被一组平行线所截,所得的对应线段成比例
推论
平行于三角形一边的直线截其他两边,所得的对应线段成比例
基本事实
平行线分线段成比例
第3章 图形的相似
3.2 平行线分线段成比例
在四条线段中, 如果其中两条线段的比等于另外两条线段的比, 那么这四条线段叫作成比例线段, 简称为比例线段.
平行四边形、矩形、正方形、菱形中的四条线段分别是成比例线段.
知识回顾
互相平行
下图是一架梯子的示意图,请根据生活常识判断AA1,BB1,CC1,DD1的位置关系.
获取新知
a
b
c
下图是一架梯子的示意图,由生活常识可以道:AA1,BB1,CC1,DD1互相平行,且若AB=BC,你能猜想出什么结果呢?
a
b
c
如图,已知直线a∥b∥c.直线l1,l2被直线a,b,c截得的线段分别为AB,BC和A1B1,B1C1,且AB=BC,要证明A1B1=B1C1,能不做辅助线证明吗?如果必须做辅助线,你考虑怎么做呢?
由于a//b//c,l3//l2,因此由“夹在两平行线间的平行线段相等”可知A2B=A1B1,BC2=B1C1.
a
b
c
过点B作直线l3//l2,分别与直线a,c相交于点A2,C2,
在△BAA2和△BCC2中:
∠ABA2=∠CBC2,BA=BC,∠BAA2=∠BCC2,
因此△BAA2≌△BCC2,从而BA2=BC2,
所以A1B1=B1C1.
两条直线被一组平行线所截,如果在其中一条直线上截得的线段相等,那么在另一条直线上截得的线段也相等.
归纳总结
a
b
c
相等,都等于1.
如图,任意画两条直线l1,l2.再画三条与l1,l2相交的平行线a,b,c,分别度量l1,l2被直线a,b,c截得的线段AB,BC,A1B1,B1C1,若AB=BC,请问 与 相等吗
平移直线c,若 ,请问 与 还相等吗
证明: ,则把线段AB二等分,分点为D.
过点D作直线d∥a,交l2于点D1.如图:
把线段BC三等分,三等分点为E,F,分别过点E,F作直线e∥a,f∥a,分别交l2于点E1,F1.
e
a
b
c
f
d
e
a
b
c
f
d
若条件“ ”改为“ ”(其中m,n是正整数),请问 的结果是什么呢?
a
b
c
两条直线被一组平行线所截,所得的对应线段成比例.
我们把以上基本事实简称为平行线分线段成比例.
归纳总结
平行于三角形一边的直线截其他两边所得的对应线段成比例.
归纳总结
例 如图,已AA1//BB1//CC1,AB=2,BC=3,A1B1=1.5, 求B1C1的长.
例题讲解
解:由平行线段成比例可知,
,即 ,
因此,
1.如图,AC,BD相交于点O,直线MN过点O,且BA//MN//CD,已知OA=3,OB=1,OD=2,求OC的长.
解:
∵ BA//MN//CD,
∴ ,
∵ OA=3,OB=1,OD=2,
∴ ,
∴ OC=6.
随堂演练
2.如图,点D,E分别在△ABC的边AB,AC上,且DE∥BC,若AB=3,AD=2,EC=1.8,求AC的长.
解:∵ DE//BC,
∴ ,
∵ AB=3,AD=2,
∴ DB=1,
∴ ,
∴ AE=3.6,
∴ AC=3.6+1.8=5.4.
课堂小结
两条直线被一组平行线所截,所得的对应线段成比例
推论
平行于三角形一边的直线截其他两边,所得的对应线段成比例
基本事实
平行线分线段成比例
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
