湘教版九年级上册3.4.1 相似三角形的判定的基本定理课件(共14张PPT)
文档属性
| 名称 | 湘教版九年级上册3.4.1 相似三角形的判定的基本定理课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 440.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
3.4.1 第1课时 相似三角形判定的基本定理
相似三角形的性质:
相似三角形的对应角相等,对应边成比例.
我们把三个角对应相等,且三条边对应成比例的两个三角形叫作相似三角形.
知识回顾
A
B
C
C'
B'
A'
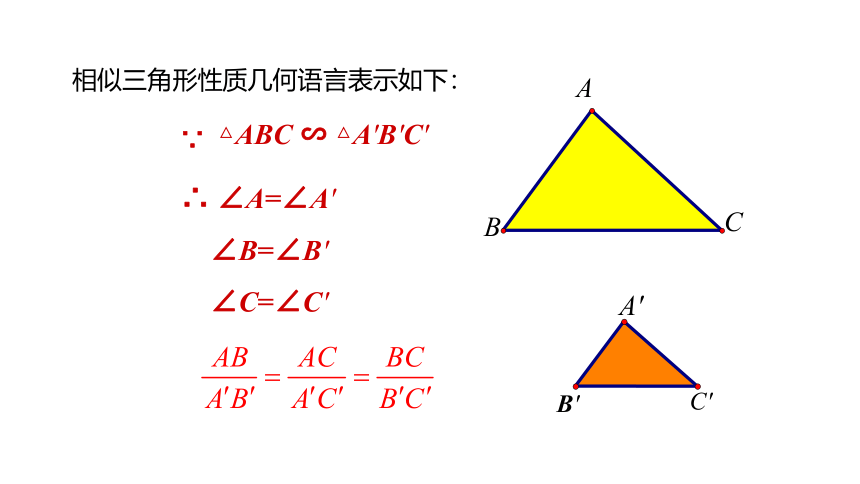
△ABC ∽ △A'B'C'
∵
∴ ∠A=∠A'
∠B=∠B'
∠C=∠C'
相似三角形性质几何语言表示如下:
定义 判定方法 全等三角形
相似三角形
三角、三边对应相等的两个三角形全等
三角对应相等, 三边对应成比例的两个三角形相似
角边角
ASA
角角边
AAS
边边边
SSS
边角边
SAS
斜边与直角边
HL
判定两个三角形相似,是不是也有这么多种方法呢?
情景导入
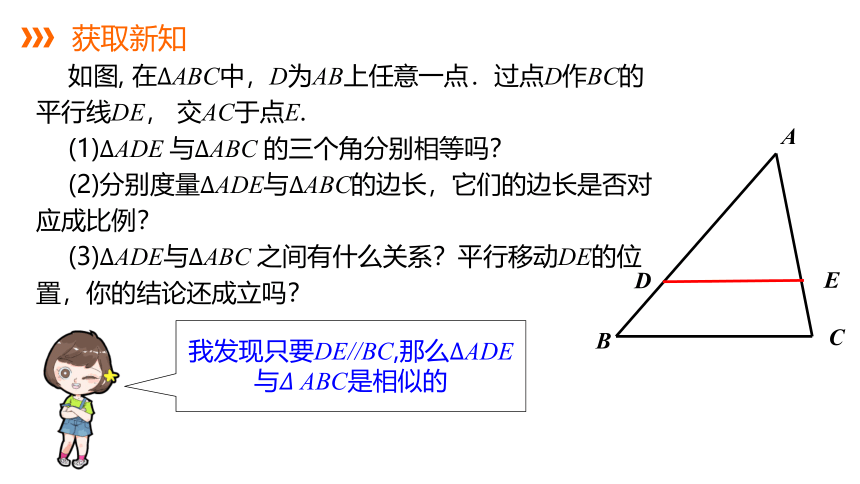
如图, 在ABC中,D为AB上任意一点.过点D作BC的平行线DE, 交AC于点E.
(1)ADE 与ABC 的三个角分别相等吗?
(2)分别度量ADE与ABC的边长,它们的边长是否对应成比例?
(3)ADE与ABC 之间有什么关系?平行移动DE的位置,你的结论还成立吗?
我发现只要DE//BC,那么ADE与ABC是相似的
A
B
C
D
E
获取新知
证明过程如下:
在ADE 与ABC中, ∵DE//BC,
∴,
过点D作DF//AC,交BC于点F.
∵ DE//BC ,DF//AC,
∴ , .
∵四边形DFCE为平行四边形,
∴ DE=FC,∴ .
∴ ADE ∽ ABC .
A
B
C
D
E
F
平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似.
A
B
C
D
E
在△ABC中,∵DE∥BC,
∴△ADE∽△ABC.
你还能画出其他图形吗?
归纳总结
几何语言:
A
B
C
D
E
∵DE∥BC,
∴△ADE∽△ABC.
点拨
D
E
A
C
B
D、E分别在
AB、AC的延长线上
D、E分别在
AB、AC的反向延长线上
平行于三角形一边的直线,与其他两边的延长线相交,截得的三角形与原三角形相似.
例1 在△ABC中,已知点D,E分别是AB,AC边的中点.
求证: △ ADE∽△ ABC.
∥BC,
ADE ∽ ABC.
A
C
B
D
E
例题讲解
例2 点D为△ABC的边AB的中点,过点D作DE ∥ BC交AC于点E.延长DE至点F,使DE=EF.
求证:△CFE∽△ ABC.
DE // BC
DE // BC,
△ ADE∽△ ABC.
△ CFE∽△ ABC.
A
B
C
D
E
F
随堂演练
1.如图,点P是平行四边形ABCD的边AB上一点,射线CP交DA的延长线于点E,则图中相似的三角形有( )
A.0对 B.1对 C.2对 D.3对
D
2.如图,在△ABC中,已知DE∥BC,AD=4,DB=8,DE=3.
求BC的长.
解:∵DE∥BC,
∴△ADE∽△ABC,
∴BC=9
3. 如图,E 是 ABCD的边AD上一点,且 ,CE交BD于F, BF=15 cm,求DF 的长.
解:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∵AD∥BC,∴△DEF∽△BCF,
又∵BF=15 cm,∴DF=6 cm.
判定三角形相似的预备定理(平行截相似)
平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形 .
[点拨] 平行于三角形一边的直线,与其他两边的延长线相交,截得的三角形与原三角形相似.
相似
课堂小结
3.4.1 第1课时 相似三角形判定的基本定理
相似三角形的性质:
相似三角形的对应角相等,对应边成比例.
我们把三个角对应相等,且三条边对应成比例的两个三角形叫作相似三角形.
知识回顾
A
B
C
C'
B'
A'
△ABC ∽ △A'B'C'
∵
∴ ∠A=∠A'
∠B=∠B'
∠C=∠C'
相似三角形性质几何语言表示如下:
定义 判定方法 全等三角形
相似三角形
三角、三边对应相等的两个三角形全等
三角对应相等, 三边对应成比例的两个三角形相似
角边角
ASA
角角边
AAS
边边边
SSS
边角边
SAS
斜边与直角边
HL
判定两个三角形相似,是不是也有这么多种方法呢?
情景导入
如图, 在ABC中,D为AB上任意一点.过点D作BC的平行线DE, 交AC于点E.
(1)ADE 与ABC 的三个角分别相等吗?
(2)分别度量ADE与ABC的边长,它们的边长是否对应成比例?
(3)ADE与ABC 之间有什么关系?平行移动DE的位置,你的结论还成立吗?
我发现只要DE//BC,那么ADE与ABC是相似的
A
B
C
D
E
获取新知
证明过程如下:
在ADE 与ABC中, ∵DE//BC,
∴,
过点D作DF//AC,交BC于点F.
∵ DE//BC ,DF//AC,
∴ , .
∵四边形DFCE为平行四边形,
∴ DE=FC,∴ .
∴ ADE ∽ ABC .
A
B
C
D
E
F
平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似.
A
B
C
D
E
在△ABC中,∵DE∥BC,
∴△ADE∽△ABC.
你还能画出其他图形吗?
归纳总结
几何语言:
A
B
C
D
E
∵DE∥BC,
∴△ADE∽△ABC.
点拨
D
E
A
C
B
D、E分别在
AB、AC的延长线上
D、E分别在
AB、AC的反向延长线上
平行于三角形一边的直线,与其他两边的延长线相交,截得的三角形与原三角形相似.
例1 在△ABC中,已知点D,E分别是AB,AC边的中点.
求证: △ ADE∽△ ABC.
∥BC,
ADE ∽ ABC.
A
C
B
D
E
例题讲解
例2 点D为△ABC的边AB的中点,过点D作DE ∥ BC交AC于点E.延长DE至点F,使DE=EF.
求证:△CFE∽△ ABC.
DE // BC
DE // BC,
△ ADE∽△ ABC.
△ CFE∽△ ABC.
A
B
C
D
E
F
随堂演练
1.如图,点P是平行四边形ABCD的边AB上一点,射线CP交DA的延长线于点E,则图中相似的三角形有( )
A.0对 B.1对 C.2对 D.3对
D
2.如图,在△ABC中,已知DE∥BC,AD=4,DB=8,DE=3.
求BC的长.
解:∵DE∥BC,
∴△ADE∽△ABC,
∴BC=9
3. 如图,E 是 ABCD的边AD上一点,且 ,CE交BD于F, BF=15 cm,求DF 的长.
解:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∵AD∥BC,∴△DEF∽△BCF,
又∵BF=15 cm,∴DF=6 cm.
判定三角形相似的预备定理(平行截相似)
平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形 .
[点拨] 平行于三角形一边的直线,与其他两边的延长线相交,截得的三角形与原三角形相似.
相似
课堂小结
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
