湘教版九年级上册3.6 位似图形的概念及画法(第1课时 )课件(共16张PPT)
文档属性
| 名称 | 湘教版九年级上册3.6 位似图形的概念及画法(第1课时 )课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 545.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 18:38:05 | ||
图片预览


文档简介
(共16张PPT)
第3章 图形的相似
3.6 第1课时 位似图形的概念及画法
如何把一个图形放大或缩小?
这节课我们来学习一种简单可行的方法.
情景引入
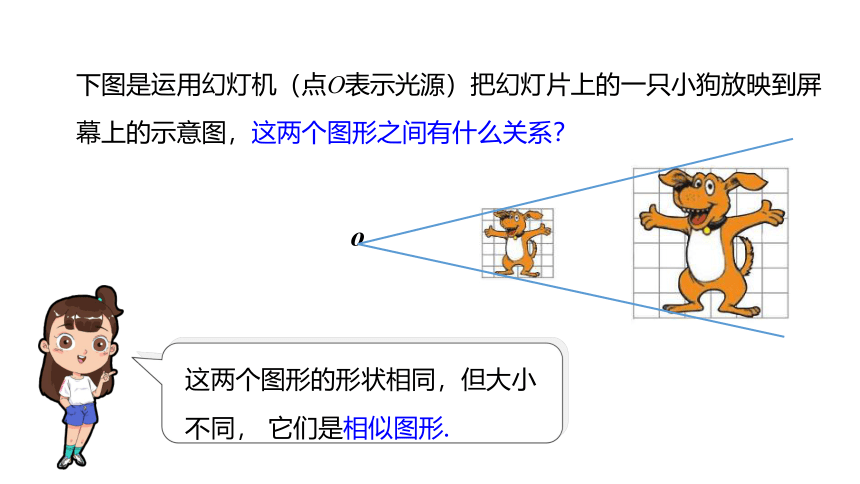
下图是运用幻灯机(点O表示光源)把幻灯片上的一只小狗放映到屏幕上的示意图,这两个图形之间有什么关系?
o
这两个图形的形状相同,但大小不同, 它们是相似图形.
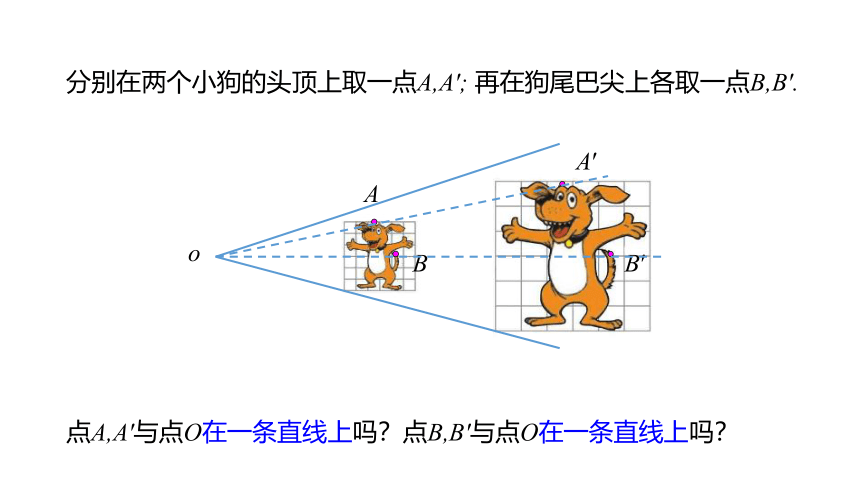
分别在两个小狗的头顶上取一点A,A′; 再在狗尾巴尖上各取一点B,B′.
o
B′
B
A′
A
点A,A′与点O在一条直线上吗?点B,B′与点O在一条直线上吗?
分别量出线段OA,OA′, OB,OB′ 的长度,计算(精确到0.1):
继续在左、右两只小狗上找出一些对应点,考察每一对对应点是否都与点O在一条直线上;
计算每一对对应点与点O所连的线段比,看它们是否与上述 ,
相等.
获取新知
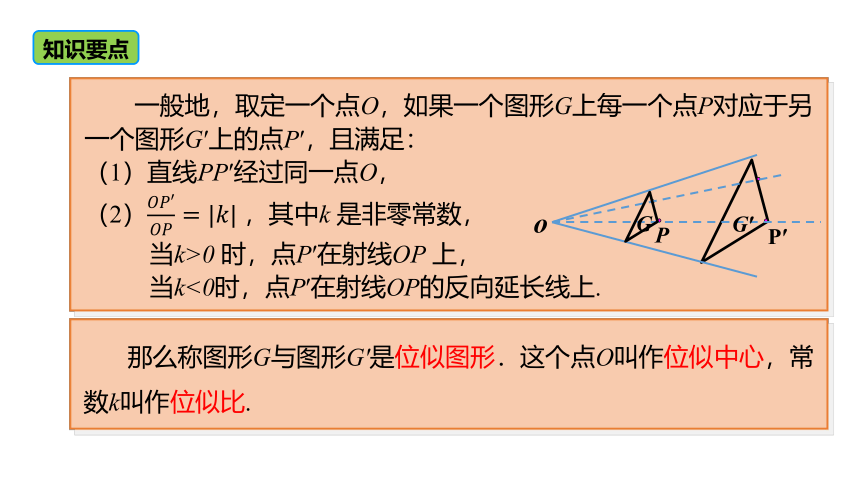
一般地,取定一个点O,如果一个图形G上每一个点P对应于另一个图形G′上的点P′,且满足:
(1)直线PP′经过同一点O,
(2) ,其中k 是非零常数,
当k>0 时,点P′在射线OP 上,
当k<0时,点P′在射线OP的反向延长线上.
那么称图形G与图形G′是位似图形.这个点O叫作位似中心,常数k叫作位似比.
o
P′
P
G
G′
知识要点
o
B
A
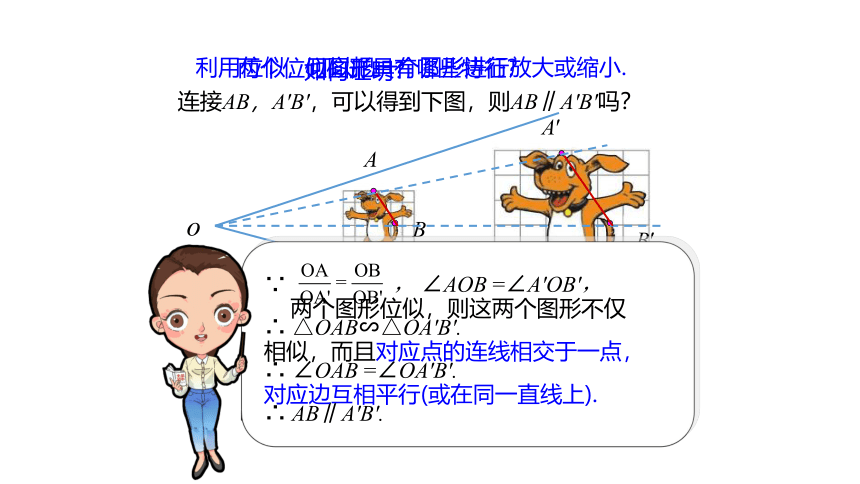
连接AB,A′B′,可以得到下图,则AB∥A′B′吗?
B′
A′
∵ , ∠AOB =∠A′OB′,
∴ △OAB∽△OA′B′.
∴ ∠OAB =∠OA′B′.
∴ AB∥A′B′.
两个位似图形具有哪些特征?
两个图形位似,则这两个图形不仅相似,而且对应点的连线相交于一点,对应边互相平行(或在同一直线上).
如何证明?
利用位似,可以把一个图形进行放大或缩小.
位似图形有以下性质:
1. 位似图形是一种特殊的相似图形,它具有相似图形的所有性质,即对应角相等,对应边的比相等.
2. 位似图形上任意一对对应点到位似中心的距离之比等于相似比.(位似图形的相似比也叫做位似比)
3. 对应线段互相平行或在同一条直线上.
归纳总结
例1 如图,已知△ABC,以点O为位似中心画△DEF,使它与△ABC位似,且位似比为2.
解:如图,画射线OA,OB,OC,
在射线OA,OB,OC上分别取点D,E,F,使OD=2OA,OE=2OB,OF=2OC,
顺次连接D,E,F,
则△ DEF与△ABC位似,位似比为2.
A
B
F
E
D
O
满足条件△DEF可以在点O的另一侧吗?
例题讲解
A
B
A’
C’
B’
C
O
例2 利用位似把△ABC缩小为原来的一半.
(1)在三角形外选一点O;
(2)过点O分别作射线OA、OB、OC;
步骤:
(4)顺次连结A’、B’、C’,所得图形就是所求作图形.
还有其他方法吗?
(3)在OA、OB、OC上分别选取A’、B’、C’,使
;
A
B
A’
C’
B’
C
O
画法二:△ABC与△A′B′C′在点O两侧:
O
A
B
C
A’
B’
C’
画法三:点O在△ABC内部:
位似作图时要注意:
①首先确定位似中心,位似中心的位置可随意选择.
②确定原图形的关键点,如四边形有四个关键点,即它的四个顶点.
③确定位似比,根据位似比的取值,可以判断是将一个图形放大还是缩小.
④符合要求的图形不唯一,因为所作的图形与所确定的位似中心的位置有关,并且同一个位似中心的两侧各有一个符合要求的图形.
2. 分别在线段OA、OB、OC、OD上
取点A'、B'、C'、D',使得
3. 顺次连接点A’ 、B’、C ’ 、D’,所得四边形A'B'C'D'就是所要求的图形.
O
D
A
B
C
A'
B'
C'
D'
1、把四边形ABCD缩小到原来的一半.
1. 在四边形外任选一点O(如图),
步骤:
随堂演练
2. 如图:以O为位似中心,将△ABC放大为原来的2倍.
A''
C''
B''
A'
C'
B'
B
C
A
O
位似图形的概念及画法
位似图形的概念
注意:形状+位置
位似图形的性质
画位似图形
注意:位似中心以及图形的相对位置
课堂小结
第3章 图形的相似
3.6 第1课时 位似图形的概念及画法
如何把一个图形放大或缩小?
这节课我们来学习一种简单可行的方法.
情景引入
下图是运用幻灯机(点O表示光源)把幻灯片上的一只小狗放映到屏幕上的示意图,这两个图形之间有什么关系?
o
这两个图形的形状相同,但大小不同, 它们是相似图形.
分别在两个小狗的头顶上取一点A,A′; 再在狗尾巴尖上各取一点B,B′.
o
B′
B
A′
A
点A,A′与点O在一条直线上吗?点B,B′与点O在一条直线上吗?
分别量出线段OA,OA′, OB,OB′ 的长度,计算(精确到0.1):
继续在左、右两只小狗上找出一些对应点,考察每一对对应点是否都与点O在一条直线上;
计算每一对对应点与点O所连的线段比,看它们是否与上述 ,
相等.
获取新知
一般地,取定一个点O,如果一个图形G上每一个点P对应于另一个图形G′上的点P′,且满足:
(1)直线PP′经过同一点O,
(2) ,其中k 是非零常数,
当k>0 时,点P′在射线OP 上,
当k<0时,点P′在射线OP的反向延长线上.
那么称图形G与图形G′是位似图形.这个点O叫作位似中心,常数k叫作位似比.
o
P′
P
G
G′
知识要点
o
B
A
连接AB,A′B′,可以得到下图,则AB∥A′B′吗?
B′
A′
∵ , ∠AOB =∠A′OB′,
∴ △OAB∽△OA′B′.
∴ ∠OAB =∠OA′B′.
∴ AB∥A′B′.
两个位似图形具有哪些特征?
两个图形位似,则这两个图形不仅相似,而且对应点的连线相交于一点,对应边互相平行(或在同一直线上).
如何证明?
利用位似,可以把一个图形进行放大或缩小.
位似图形有以下性质:
1. 位似图形是一种特殊的相似图形,它具有相似图形的所有性质,即对应角相等,对应边的比相等.
2. 位似图形上任意一对对应点到位似中心的距离之比等于相似比.(位似图形的相似比也叫做位似比)
3. 对应线段互相平行或在同一条直线上.
归纳总结
例1 如图,已知△ABC,以点O为位似中心画△DEF,使它与△ABC位似,且位似比为2.
解:如图,画射线OA,OB,OC,
在射线OA,OB,OC上分别取点D,E,F,使OD=2OA,OE=2OB,OF=2OC,
顺次连接D,E,F,
则△ DEF与△ABC位似,位似比为2.
A
B
F
E
D
O
满足条件△DEF可以在点O的另一侧吗?
例题讲解
A
B
A’
C’
B’
C
O
例2 利用位似把△ABC缩小为原来的一半.
(1)在三角形外选一点O;
(2)过点O分别作射线OA、OB、OC;
步骤:
(4)顺次连结A’、B’、C’,所得图形就是所求作图形.
还有其他方法吗?
(3)在OA、OB、OC上分别选取A’、B’、C’,使
;
A
B
A’
C’
B’
C
O
画法二:△ABC与△A′B′C′在点O两侧:
O
A
B
C
A’
B’
C’
画法三:点O在△ABC内部:
位似作图时要注意:
①首先确定位似中心,位似中心的位置可随意选择.
②确定原图形的关键点,如四边形有四个关键点,即它的四个顶点.
③确定位似比,根据位似比的取值,可以判断是将一个图形放大还是缩小.
④符合要求的图形不唯一,因为所作的图形与所确定的位似中心的位置有关,并且同一个位似中心的两侧各有一个符合要求的图形.
2. 分别在线段OA、OB、OC、OD上
取点A'、B'、C'、D',使得
3. 顺次连接点A’ 、B’、C ’ 、D’,所得四边形A'B'C'D'就是所要求的图形.
O
D
A
B
C
A'
B'
C'
D'
1、把四边形ABCD缩小到原来的一半.
1. 在四边形外任选一点O(如图),
步骤:
随堂演练
2. 如图:以O为位似中心,将△ABC放大为原来的2倍.
A''
C''
B''
A'
C'
B'
B
C
A
O
位似图形的概念及画法
位似图形的概念
注意:形状+位置
位似图形的性质
画位似图形
注意:位似中心以及图形的相对位置
课堂小结
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
