湘教版九年级上册2.1 一元二次方程(共16张PPT)
文档属性
| 名称 | 湘教版九年级上册2.1 一元二次方程(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 263.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
第2章 一元二次方程
2.1 一元二次方程
什么是方程?什么是方程的解(或根)?
含有未知数的等式叫做方程。
使方程两边成立的未知数的值叫做方程的解。
我们曾学过哪些方程?
分式方程,一元一次方程,二元一次方程。
什么叫做一元一次方程?
知识回顾
只含有一个未知数,且未知数的次数为1的方程叫做一元一次方程
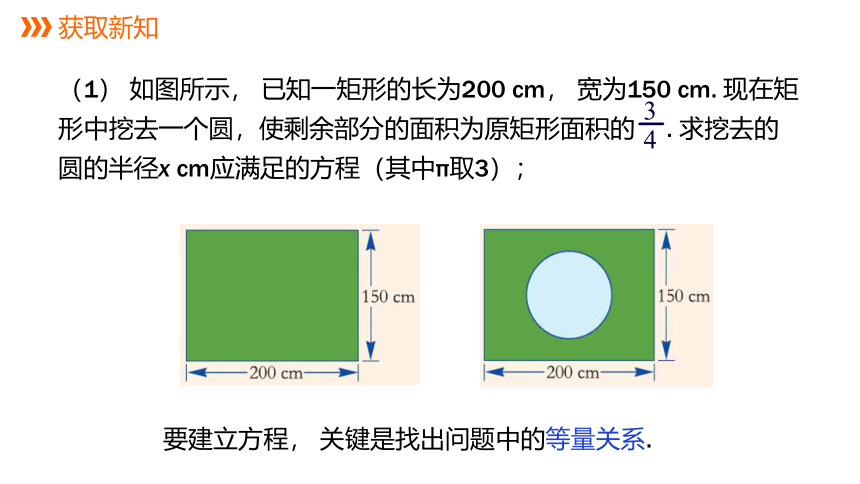
(1) 如图所示, 已知一矩形的长为200 cm, 宽为150 cm. 现在矩形中挖去一个圆,使剩余部分的面积为原矩形面积的 . 求挖去的圆的半径x cm应满足的方程(其中π取3);
要建立方程, 关键是找出问题中的等量关系.
获取新知
问题(1)涉及的等量关系是:
矩形的面积-圆的面积=矩形的面积× .
由于圆的半径为x cm, 则它的面积为3x2 cm2.
根据等量关系, 可以列出方程
200 × 150 - 3x2 = 200 × 150 × .
化简, 整理得
x2 - 2500 = 0.
①
题目涉及的等量关系分别是:
化简, 整理得
设该市两年来汽车拥有量的年平均增长率为x.
根据等量关系, 可以列出方程
75 (1 + x )2 = 108.
25x2 + 50x - 11 = 0.
②
(2)据某市交通部门统计,前年该市汽车拥有量为75万辆,两年后增加到108万辆.求该市两年来汽车拥有量的年平均增长率x应满足的方程.
两年后的汽车拥有量=前年的汽车拥有量× (1 +年平均增长率)2.
方程①②中有几个未知数?
它们的左边是x的几次多项式?
x2 - 2500 =0
①
25x2 + 50x – 11=0.
②
回忆一元一次方程的概念,以上的方程①②是一元一次方程么?若不是那么它们又是什么方程呢?
如果一个方程通过整理可以使右边为0, 而左边是只含有一个未知数的二次多项式, 那么这样的方程叫作一元二次方程。
其中a, b, c分别叫作二次项系数、一次项系数、常数项.
它的一般形式是
ax2+bx+c=0 (a ,b,c 是已知数, a ≠0),
在写一元二次方程的一般形式时,通常按未知数的次数从高到低排列,即先写二次项,再写一次项,最后是常数项。
一元二次方程
概念认知
判断下列方程是否为一元二次方程:
① 10x2=9 ( ) ②2(x-1)=3x ( )
③2x2-3x-1=0 ( ) ④ ( )
⑤2xy-7=0 ( ) ⑥9x2=5-4x ( )
⑦4x2=5x ( ) ⑧3y2+4=5y ( )
√
√
√
√
×
×
×
√
( )
⑨
×
辨一辨
一元二次方程的特点:
注意:判断一个方程未知数的最高次数是不是2次必须要将原方程化简后再判断.
(2)只含有一个未知数;
(3)化简后未知数最高次数为2次.
(1)两边都是整式;
归纳总结
例 下列方程是否为一元二次方程? 若是, 指出其中的二次项系数、一次项系数和常数项.
(1) 3x (1 – x ) + 10 = 2( x + 2);
(2) 5x ( x + 1) + 7 = 5x2 - 4.
根据一元二次方程的概念,以上的方程都需要进行整理,使右边为0,再根据左边的式子进行判断.
例题讲解
(1) 3x (1 – x ) + 10 = 2( x + 2)
去括号, 得
3x - 3x2 + 10 = 2x + 4.
移项, 合并同类项, 得
- 3x2 + x + 6 = 0,
这是一元二次方程,
二次项系数是-3,
一次项系数是1,
常数项是6.
思考:
可以写成3x2 - x -6 = 0 吗?那么各项系数又是多少?常数项是多少呢?
去括号, 得
移项, 合并同类项, 得
这是一元一次方程, 不是一元二次方程.
(2) 5x ( x + 1) + 7 = 5x2 - 4.
5x2 + 5x + 7 = 5x2 - 4.
5x + 11 = 0,
1.请用线把左边的方程与右边所对应的方程类型连接起来:
2x2+ 5x = x2- 3
(x + 1)2- 1 = x2+ 4
3x + 5 = 2x - 1
一元一次方程
一元二次方程
分式方程
随堂演练
2
-1
-3
1
-7
3
3
0
2
3. 两年前生产1吨某种药品的成本是6000元.随着生产技术的进步,现在生产1吨这种药品的成本是3600元,试求这种药品成本的年平均下降率?
若设这种药品的年平均下降率为x,根据题意,列方程为 .
6000 ( 1-x )2 = 3600
一元二次方程
概念
是整式方程;
含一个未知数;
化简后未知数最高次数是2.
一般
形式
ax2+bx+c=0 (a ≠0)
课堂小结
第2章 一元二次方程
2.1 一元二次方程
什么是方程?什么是方程的解(或根)?
含有未知数的等式叫做方程。
使方程两边成立的未知数的值叫做方程的解。
我们曾学过哪些方程?
分式方程,一元一次方程,二元一次方程。
什么叫做一元一次方程?
知识回顾
只含有一个未知数,且未知数的次数为1的方程叫做一元一次方程
(1) 如图所示, 已知一矩形的长为200 cm, 宽为150 cm. 现在矩形中挖去一个圆,使剩余部分的面积为原矩形面积的 . 求挖去的圆的半径x cm应满足的方程(其中π取3);
要建立方程, 关键是找出问题中的等量关系.
获取新知
问题(1)涉及的等量关系是:
矩形的面积-圆的面积=矩形的面积× .
由于圆的半径为x cm, 则它的面积为3x2 cm2.
根据等量关系, 可以列出方程
200 × 150 - 3x2 = 200 × 150 × .
化简, 整理得
x2 - 2500 = 0.
①
题目涉及的等量关系分别是:
化简, 整理得
设该市两年来汽车拥有量的年平均增长率为x.
根据等量关系, 可以列出方程
75 (1 + x )2 = 108.
25x2 + 50x - 11 = 0.
②
(2)据某市交通部门统计,前年该市汽车拥有量为75万辆,两年后增加到108万辆.求该市两年来汽车拥有量的年平均增长率x应满足的方程.
两年后的汽车拥有量=前年的汽车拥有量× (1 +年平均增长率)2.
方程①②中有几个未知数?
它们的左边是x的几次多项式?
x2 - 2500 =0
①
25x2 + 50x – 11=0.
②
回忆一元一次方程的概念,以上的方程①②是一元一次方程么?若不是那么它们又是什么方程呢?
如果一个方程通过整理可以使右边为0, 而左边是只含有一个未知数的二次多项式, 那么这样的方程叫作一元二次方程。
其中a, b, c分别叫作二次项系数、一次项系数、常数项.
它的一般形式是
ax2+bx+c=0 (a ,b,c 是已知数, a ≠0),
在写一元二次方程的一般形式时,通常按未知数的次数从高到低排列,即先写二次项,再写一次项,最后是常数项。
一元二次方程
概念认知
判断下列方程是否为一元二次方程:
① 10x2=9 ( ) ②2(x-1)=3x ( )
③2x2-3x-1=0 ( ) ④ ( )
⑤2xy-7=0 ( ) ⑥9x2=5-4x ( )
⑦4x2=5x ( ) ⑧3y2+4=5y ( )
√
√
√
√
×
×
×
√
( )
⑨
×
辨一辨
一元二次方程的特点:
注意:判断一个方程未知数的最高次数是不是2次必须要将原方程化简后再判断.
(2)只含有一个未知数;
(3)化简后未知数最高次数为2次.
(1)两边都是整式;
归纳总结
例 下列方程是否为一元二次方程? 若是, 指出其中的二次项系数、一次项系数和常数项.
(1) 3x (1 – x ) + 10 = 2( x + 2);
(2) 5x ( x + 1) + 7 = 5x2 - 4.
根据一元二次方程的概念,以上的方程都需要进行整理,使右边为0,再根据左边的式子进行判断.
例题讲解
(1) 3x (1 – x ) + 10 = 2( x + 2)
去括号, 得
3x - 3x2 + 10 = 2x + 4.
移项, 合并同类项, 得
- 3x2 + x + 6 = 0,
这是一元二次方程,
二次项系数是-3,
一次项系数是1,
常数项是6.
思考:
可以写成3x2 - x -6 = 0 吗?那么各项系数又是多少?常数项是多少呢?
去括号, 得
移项, 合并同类项, 得
这是一元一次方程, 不是一元二次方程.
(2) 5x ( x + 1) + 7 = 5x2 - 4.
5x2 + 5x + 7 = 5x2 - 4.
5x + 11 = 0,
1.请用线把左边的方程与右边所对应的方程类型连接起来:
2x2+ 5x = x2- 3
(x + 1)2- 1 = x2+ 4
3x + 5 = 2x - 1
一元一次方程
一元二次方程
分式方程
随堂演练
2
-1
-3
1
-7
3
3
0
2
3. 两年前生产1吨某种药品的成本是6000元.随着生产技术的进步,现在生产1吨这种药品的成本是3600元,试求这种药品成本的年平均下降率?
若设这种药品的年平均下降率为x,根据题意,列方程为 .
6000 ( 1-x )2 = 3600
一元二次方程
概念
是整式方程;
含一个未知数;
化简后未知数最高次数是2.
一般
形式
ax2+bx+c=0 (a ≠0)
课堂小结
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
