湘教版数学九年级上册 1.2 第1课时 反比例函数y=k/x(k>0)的图象与性质 同步课件 (共17张PPT)
文档属性
| 名称 | 湘教版数学九年级上册 1.2 第1课时 反比例函数y=k/x(k>0)的图象与性质 同步课件 (共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 564.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
第1章 反比例函数
1.2 第1课时 反比例函数 y= (k>0)的图象与性质
什么是反比例函数?
一般地,如果两个变量y 与x的关系可以表示成y = ( k是常数, k ≠ 0 ) 的函数叫做反比例函数.其中k称为反比例函数的反比例系数.
知识回顾
我们已经学习了用“ ”画一次函数的图象,
并且知道一次函数的图象是 。
那么怎样画反比例函数 (k为常数,k ≠0)的图象呢?
描点法
一条直线
反比例函数的图象是什么形状的?
它的图象又有什么规律和性质?
带着这些疑问我们开始下面的学习。。。
情景导入
反比例函数 (k为常数,k≠0)的图象是什么样子呢?
我们先将k取为6,画出反比例函数的图象并进行观察.
获取新知
如何画反比例函数 的图象?
描点法步骤:
列表
描点
连线
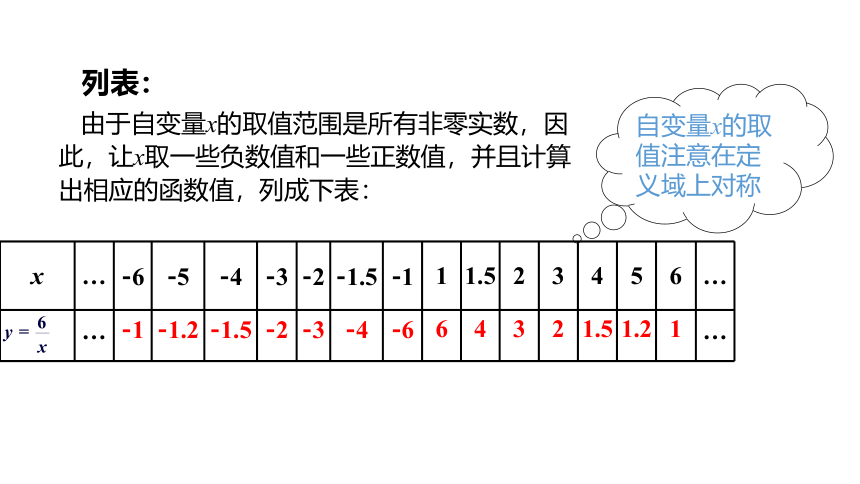
由于自变量x的取值范围是所有非零实数,因此,让x取一些负数值和一些正数值,并且计算出相应的函数值,列成下表:
x … -6 -5 -4 -3 -2 -1.5 -1 1 1.5 2 3 4 5 6 …
… -1 -1.2 -1.5 -2 -3 -4 -6 6 4 3 2 1.5 1.2 1 …
自变量x的取值注意在定义域上对称
列表:
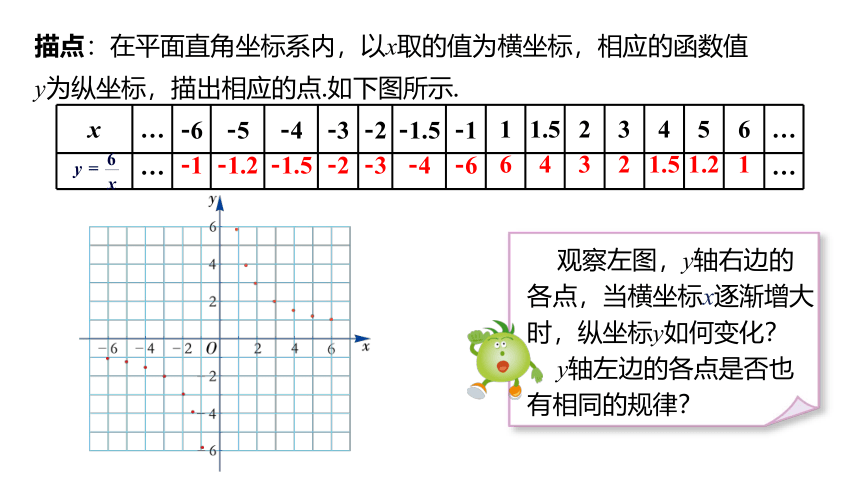
描点:在平面直角坐标系内,以x取的值为横坐标,相应的函数值y为纵坐标,描出相应的点.如下图所示.
观察左图,y轴右边的
各点,当横坐标x逐渐增大
时,纵坐标y如何变化?
y轴左边的各点是否也
有相同的规律?
x … -6 -5 -4 -3 -2 -1.5 -1 1 1.5 2 3 4 5 6 …
… -1 -1.2 -1.5 -2 -3 -4 -6 6 4 3 2 1.5 1.2 1 …
当x>0时,函数值y随自变量x的增大而减小;
当x<0时,也有这一规律.
我们可以证明:对于反比例函数 ,
连线:根据以上分析,我们可以把y轴右边各点和左边各点,分别用一条光滑曲线顺次连接起来.
从 看出,x取任意非零实数,都有y≠0,因此这两支曲线与x轴都不相交.由于x不能取0 ,因此这两支曲线与y轴也都不相交.
这样就画出了 的图象,
如右图所示.
在右图所示的直角坐标系内,画出反比例函数 的图象.
例题讲解
例1 画反比例函数 的图象.
让x取一些非零实数,并计算出相应的函数值y, 列成下表.
解 列表:
x … -5 -4 -3 -2 -1.5 -1 1 1.5 2 3 4 5 …
… -0.6 -0.75 -1 -1.5 -2 -3 3 2 1.5 1 0.75 0.6 …
在平面直角坐标系内,以x取的值为横坐标,相应的函数值y为纵坐标,描出相应的点.
描点:
●
●
●
●
●
●
●
●
●
●
●
●
x … -5 -4 -3 -2 -1.5 -1 1 1.5 2 3 4 5 …
… -0.6 -0.75 -1 -1.5 -2 -3 3 2 1.5 1 0.75 0.6 …
连线:
把y 轴左边各点和右边各点分别用一条光滑曲线顺次连接起来,就得到了函数 的图象,如右图所示.
(2)在每一象限内,函数值y随自变量x的变化如何变化?
(1)每个函数的图象分别位于哪些象限?
观察画出的 , 的图象,思考下列问题:
想一想
获取新知
对于y轴右边的点,当自变量x逐渐增大时,函数值y反而减小;对于y轴左边的点也有这一性质.
可以发现这两个函数的图象均由两支曲线组成,且分别位于第一、三象限.
归纳总结
一般地, 当k > 0 时, 反比例函数 的图象由分别在第一、三象限内的两支曲线组成, 它们与 x 轴、y 轴都不相交,在每个象限内, 函数值 y 随自变量 x 的增大而减小.
C
随堂演练
2. 画出下列反比例函数的图象:
解:如图所示:
(1)
(2)
1、如何绘制反比例函数的图象
2、反比例函数图象(k>0)的性质
课堂小结
列表,描点,连线
第1章 反比例函数
1.2 第1课时 反比例函数 y= (k>0)的图象与性质
什么是反比例函数?
一般地,如果两个变量y 与x的关系可以表示成y = ( k是常数, k ≠ 0 ) 的函数叫做反比例函数.其中k称为反比例函数的反比例系数.
知识回顾
我们已经学习了用“ ”画一次函数的图象,
并且知道一次函数的图象是 。
那么怎样画反比例函数 (k为常数,k ≠0)的图象呢?
描点法
一条直线
反比例函数的图象是什么形状的?
它的图象又有什么规律和性质?
带着这些疑问我们开始下面的学习。。。
情景导入
反比例函数 (k为常数,k≠0)的图象是什么样子呢?
我们先将k取为6,画出反比例函数的图象并进行观察.
获取新知
如何画反比例函数 的图象?
描点法步骤:
列表
描点
连线
由于自变量x的取值范围是所有非零实数,因此,让x取一些负数值和一些正数值,并且计算出相应的函数值,列成下表:
x … -6 -5 -4 -3 -2 -1.5 -1 1 1.5 2 3 4 5 6 …
… -1 -1.2 -1.5 -2 -3 -4 -6 6 4 3 2 1.5 1.2 1 …
自变量x的取值注意在定义域上对称
列表:
描点:在平面直角坐标系内,以x取的值为横坐标,相应的函数值y为纵坐标,描出相应的点.如下图所示.
观察左图,y轴右边的
各点,当横坐标x逐渐增大
时,纵坐标y如何变化?
y轴左边的各点是否也
有相同的规律?
x … -6 -5 -4 -3 -2 -1.5 -1 1 1.5 2 3 4 5 6 …
… -1 -1.2 -1.5 -2 -3 -4 -6 6 4 3 2 1.5 1.2 1 …
当x>0时,函数值y随自变量x的增大而减小;
当x<0时,也有这一规律.
我们可以证明:对于反比例函数 ,
连线:根据以上分析,我们可以把y轴右边各点和左边各点,分别用一条光滑曲线顺次连接起来.
从 看出,x取任意非零实数,都有y≠0,因此这两支曲线与x轴都不相交.由于x不能取0 ,因此这两支曲线与y轴也都不相交.
这样就画出了 的图象,
如右图所示.
在右图所示的直角坐标系内,画出反比例函数 的图象.
例题讲解
例1 画反比例函数 的图象.
让x取一些非零实数,并计算出相应的函数值y, 列成下表.
解 列表:
x … -5 -4 -3 -2 -1.5 -1 1 1.5 2 3 4 5 …
… -0.6 -0.75 -1 -1.5 -2 -3 3 2 1.5 1 0.75 0.6 …
在平面直角坐标系内,以x取的值为横坐标,相应的函数值y为纵坐标,描出相应的点.
描点:
●
●
●
●
●
●
●
●
●
●
●
●
x … -5 -4 -3 -2 -1.5 -1 1 1.5 2 3 4 5 …
… -0.6 -0.75 -1 -1.5 -2 -3 3 2 1.5 1 0.75 0.6 …
连线:
把y 轴左边各点和右边各点分别用一条光滑曲线顺次连接起来,就得到了函数 的图象,如右图所示.
(2)在每一象限内,函数值y随自变量x的变化如何变化?
(1)每个函数的图象分别位于哪些象限?
观察画出的 , 的图象,思考下列问题:
想一想
获取新知
对于y轴右边的点,当自变量x逐渐增大时,函数值y反而减小;对于y轴左边的点也有这一性质.
可以发现这两个函数的图象均由两支曲线组成,且分别位于第一、三象限.
归纳总结
一般地, 当k > 0 时, 反比例函数 的图象由分别在第一、三象限内的两支曲线组成, 它们与 x 轴、y 轴都不相交,在每个象限内, 函数值 y 随自变量 x 的增大而减小.
C
随堂演练
2. 画出下列反比例函数的图象:
解:如图所示:
(1)
(2)
1、如何绘制反比例函数的图象
2、反比例函数图象(k>0)的性质
课堂小结
列表,描点,连线
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
