简易逻辑复习小结
图片预览





文档简介
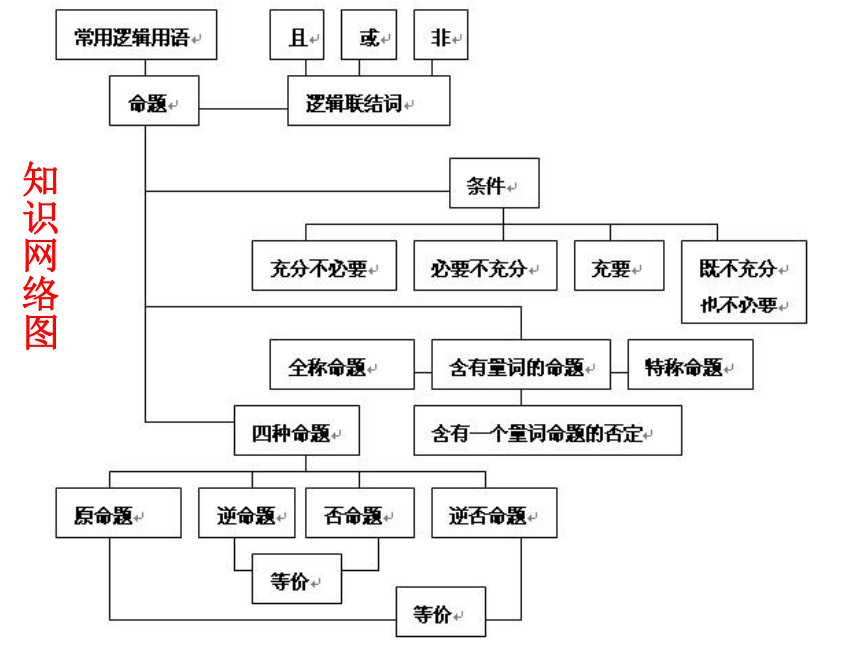
课件19张PPT。第一章《常用逻辑用语》 复习小结知识网络图 在数学中,我们把用 语言 、 符号 或 式子表达的,可以判断真假的陈述句 叫做命题.其中 判断为真 的语句叫做真命题, 判断为假 的语句叫做假命题.1.1 命题及其关系四种命题形式:
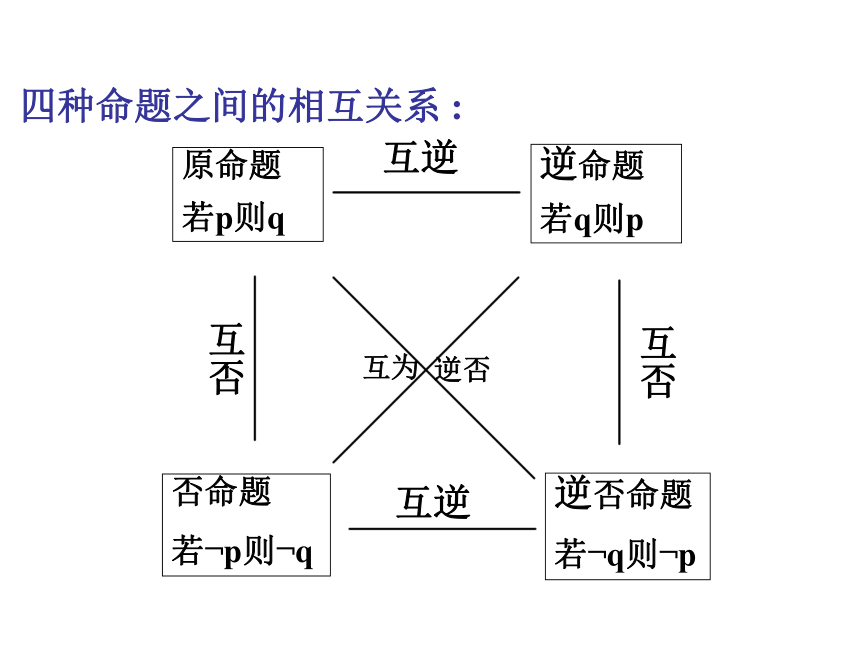
原命题:
逆命题:
否命题:
逆否命题:若 p , 则 q .
若 q , 则 p .
若 ┐p , 则 ┐q .
若 ┐q , 则 ┐p .(用p和q分别表示原命题的条件和结论,
用?p和?q分别表示p和q的否定.)一些常见词语的否定:不是不都是不大于大小于一个也没有至少有两个至多有(n-1)个至少有(n+1)个存在某x,
不成立存在某x,
成立四种命题之间的相互关系 :四种命题的真假性,有且仅有下面四种情况:(1)两个命题互为逆否命题,它们有相同的真假性;(2)两个命题为互逆命题或互否命题,它们的真假性没有关系.注意:命题的否定与否命题的区别 命题的否定:只否定命题的结论.
“若p,则q”的否定是“若p,则? q”. 否命题:同时否定命题的条件和结论.
“若p,则q”的否命题是“若? p,则? q”. 一般地,如果已知 ,即命题“若p则q” 为真命题,那么就说,p 是q 的充分条件,q 是p 的必要条件.1.2 充分条件与必要条件说明:(1)上述定义中,“p═?q” 即如果具备了条件p,就足以保证q成立,所以称p是q的充分条件.
(2)注意条件和结论是相对而言的,由于“p═?q”的等价命题是“?q═??p”,即若q不成立,则p不成立,所以称q 是p成立的必要条件.
(3)q 成立时, p可能成立,也可能不成立,即q成立不保证p一定成立. 充要条件:定义:若既有
,又有记作:则称 p是 q的充分必要条件,简称充要条件. 由上述命题的充分条件、必要条件的判断过程,可确定:命题按条件p和结论q的充分性、必要性可分为: 充分条件与必要条件的判断: (2)利用命题的对称关系判断:“p q”的等价命题是“┐q ┐p”.
即“若┐q ┐p成立,则p是q的充分条件,q是p的必要条件” .(1)直接利用定义判断:即“若p q成立,则p是q的充分条件,q是p的必要条件”.
(条件与结论是相对的)(3)利用命题的传递关系判断:“p q且 q r,则 p r”.则p是r的充分条件,r是p的必要条件”.① 从命题角度看㈠若p则q是真命题,那么p是q的充分条件
q是p的必要条件.㈡若p则q是真命题,且若q则p为假命题,那么p是q 的充分不必要条件,q是p必要不充分条件.(四)若p则q,若q则p都是假命题,那么p是q的既不充分也不必要条件,q是p既不充分也不必要条件.(三)若p则q,且若q则p都是真命题,那么p是q的 充要条件② 从集合角度看
命题“若p则q”1.3 简单的逻辑联结词:
“且”、“或”、“非”
简单命题:
不含逻辑联结词的命题.
常用小写拉丁字母 p,q,r,s,…表示.
复合命题:
由简单命题与逻辑联结词构成的命题.
构成形式:p且q; p或q;非p .(非p 也叫命题 p 的否定)分别记作:p∧q ; p∨q ; ? p .判断复合命题真假的步骤:⑴ 把复合命题写成两个简单命题,并确定复合命题的构成形式;
⑵ 判断简单命题的真假;
⑶ 利用真值表判断复合命题的真假。有真即真,全假为假.命题是“p∨q”形式: 命题是“p∧q”形式: 全真为真,有假即假.
(真假相反)要判定全称命题“ x∈M, p(x) ”是真命题,需要对集合M中每个元素x, 证明p(x)成立;如果在集合M中找到一个元素x0,使得p(x0)不成立,那么这个全称命题就是假命题.判断全称命题和特称命题真假要判定特称命题 “ x0∈M, p(x0)”是真命题,只需在集合M中找到一个元素x0,使p(x0)成立即可,如果在集合M中,使p(x)成立的元素x不存在,则特称命题是假命题.1.4 全称量词与存在量词常见的全称量词有“所有的”“任意一个” “一切” “每一个” “任给”“所有的”等.常见的存在量词有“存在一个”“至少一个” “有些” “有一个” “对某个” “有的”等.例题解析:课堂练习:课后作业3. 预习教材选修2-2第1~9页 变化率与导数1. 教辅课时作业第11页 复习小结2. 第一章《常用逻辑用语》第1,2单元
自主检测题
原命题:
逆命题:
否命题:
逆否命题:若 p , 则 q .
若 q , 则 p .
若 ┐p , 则 ┐q .
若 ┐q , 则 ┐p .(用p和q分别表示原命题的条件和结论,
用?p和?q分别表示p和q的否定.)一些常见词语的否定:不是不都是不大于大小于一个也没有至少有两个至多有(n-1)个至少有(n+1)个存在某x,
不成立存在某x,
成立四种命题之间的相互关系 :四种命题的真假性,有且仅有下面四种情况:(1)两个命题互为逆否命题,它们有相同的真假性;(2)两个命题为互逆命题或互否命题,它们的真假性没有关系.注意:命题的否定与否命题的区别 命题的否定:只否定命题的结论.
“若p,则q”的否定是“若p,则? q”. 否命题:同时否定命题的条件和结论.
“若p,则q”的否命题是“若? p,则? q”. 一般地,如果已知 ,即命题“若p则q” 为真命题,那么就说,p 是q 的充分条件,q 是p 的必要条件.1.2 充分条件与必要条件说明:(1)上述定义中,“p═?q” 即如果具备了条件p,就足以保证q成立,所以称p是q的充分条件.
(2)注意条件和结论是相对而言的,由于“p═?q”的等价命题是“?q═??p”,即若q不成立,则p不成立,所以称q 是p成立的必要条件.
(3)q 成立时, p可能成立,也可能不成立,即q成立不保证p一定成立. 充要条件:定义:若既有
,又有记作:则称 p是 q的充分必要条件,简称充要条件. 由上述命题的充分条件、必要条件的判断过程,可确定:命题按条件p和结论q的充分性、必要性可分为: 充分条件与必要条件的判断: (2)利用命题的对称关系判断:“p q”的等价命题是“┐q ┐p”.
即“若┐q ┐p成立,则p是q的充分条件,q是p的必要条件” .(1)直接利用定义判断:即“若p q成立,则p是q的充分条件,q是p的必要条件”.
(条件与结论是相对的)(3)利用命题的传递关系判断:“p q且 q r,则 p r”.则p是r的充分条件,r是p的必要条件”.① 从命题角度看㈠若p则q是真命题,那么p是q的充分条件
q是p的必要条件.㈡若p则q是真命题,且若q则p为假命题,那么p是q 的充分不必要条件,q是p必要不充分条件.(四)若p则q,若q则p都是假命题,那么p是q的既不充分也不必要条件,q是p既不充分也不必要条件.(三)若p则q,且若q则p都是真命题,那么p是q的 充要条件② 从集合角度看
命题“若p则q”1.3 简单的逻辑联结词:
“且”、“或”、“非”
简单命题:
不含逻辑联结词的命题.
常用小写拉丁字母 p,q,r,s,…表示.
复合命题:
由简单命题与逻辑联结词构成的命题.
构成形式:p且q; p或q;非p .(非p 也叫命题 p 的否定)分别记作:p∧q ; p∨q ; ? p .判断复合命题真假的步骤:⑴ 把复合命题写成两个简单命题,并确定复合命题的构成形式;
⑵ 判断简单命题的真假;
⑶ 利用真值表判断复合命题的真假。有真即真,全假为假.命题是“p∨q”形式: 命题是“p∧q”形式: 全真为真,有假即假.
(真假相反)要判定全称命题“ x∈M, p(x) ”是真命题,需要对集合M中每个元素x, 证明p(x)成立;如果在集合M中找到一个元素x0,使得p(x0)不成立,那么这个全称命题就是假命题.判断全称命题和特称命题真假要判定特称命题 “ x0∈M, p(x0)”是真命题,只需在集合M中找到一个元素x0,使p(x0)成立即可,如果在集合M中,使p(x)成立的元素x不存在,则特称命题是假命题.1.4 全称量词与存在量词常见的全称量词有“所有的”“任意一个” “一切” “每一个” “任给”“所有的”等.常见的存在量词有“存在一个”“至少一个” “有些” “有一个” “对某个” “有的”等.例题解析:课堂练习:课后作业3. 预习教材选修2-2第1~9页 变化率与导数1. 教辅课时作业第11页 复习小结2. 第一章《常用逻辑用语》第1,2单元
自主检测题
