2021—2022学年人教版数学八年级下册 20.2 数据的波动程度 课件(22张PPT)
文档属性
| 名称 | 2021—2022学年人教版数学八年级下册 20.2 数据的波动程度 课件(22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 915.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 20:34:45 | ||
图片预览








文档简介
20.2 数据的波动程度
复习回顾
根据实际情况填写:(加权平均数、中位数、众数.)
①老板进货时关注卖出商品的 .
②评委给选手综合得分时关注
③被招聘的员工关注公司员工工资的
中位数
加权平均数
众数
新知探究
(1)甜玉米的产量可用什么量来描述?请计算后说明.
说明在试验田中,甲、乙两种甜玉米的平均产量相差不大.
可估计这个地区种植这两种甜玉米的平均产量相差不大.
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
了解方差的定义和计算公式;
会用方差的计算公式比较两组数
据的波动大小.
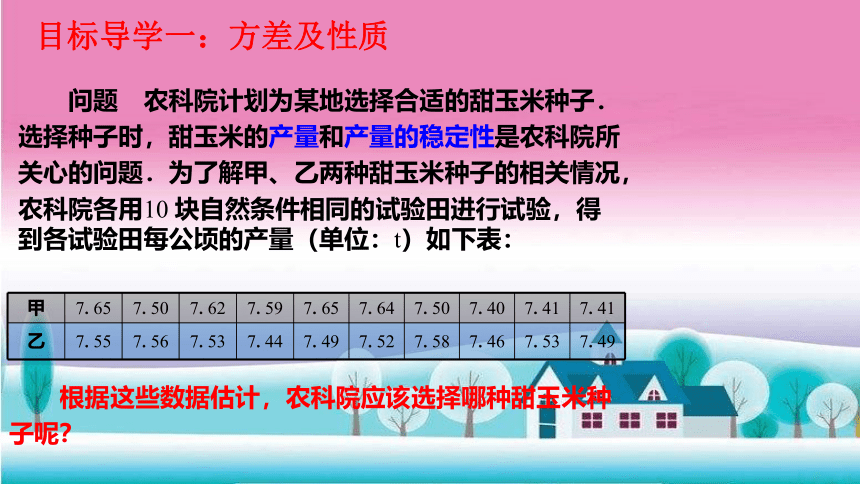
问题 农科院计划为某地选择合适的甜玉米种子.
选择种子时,甜玉米的产量和产量的稳定性是农科院所
关心的问题.为了解甲、乙两种甜玉米种子的相关情况,
农科院各用10 块自然条件相同的试验田进行试验,得到各试验田每公顷的产量(单位:t)如下表:
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
根据这些数据估计,农科院应该选择哪种甜玉米种
子呢?
目标导学一:方差及性质
2、方差的计算公式
=————————————————————
3、方差的意义
方差越大,___________越大;
方差越小,__________越小.
4.正如用样本的平均数估计总体的平均数一
样,也可以用样本的方差来估计________.
波动性
波动性
整体的方差
合作释疑
知识点一
各 数据与平均数的差的平方的平均数叫做这批数据的方差。公式为:
我们可以用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况。这个结果通常称为方差。
方差的定义及公式
新知归纳
1.方差的概念:
设有n个数据x1,x2,…,xn,各数据与它们的平均数 的差的平方分别是 ,我们用这些值的平均数,即
来衡量这组数据的波动大小,并把它叫作这组数据的方差.
解:甲、乙两团演员的身高平均数分别是
=___________________________
=_____
=____________________________
=_____
甲
乙
165
166
合作释疑
知识应用
例1:在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》, 参加表演的女演员的身高(单位:cm)
如表所示。
甲
163
164
164
165
165
166
166
167
乙
163
165
165
166
166
167
168
168
哪个芭蕾舞团女演员的身高更整齐?
精典例题
新知应用
例1: 在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团表演了舞剧《天鹅湖》,参加表演的女演员的身高(单位:cm)分别是:
{3B4B98B0-60AC-42C2-AFA5-B58CD77FA1E5}甲
163
164
164
165
165
166
166
167
乙
163
165
165
166
166
167
168
168
哪个芭蕾舞团女演员的身高更整齐?
1.数据-2,-1,0,1,2的方差是( )
A.0 B. C.2 D.4
2.在样本方差的计算式s2=10(1)[(x1-5)2+(x2-5)2+…+(x10-5)2]中,数字“10”表示__________,数字“5”表示___________.
3.在一次射击训练中,某位选手五次射击的环数分别为5,8,7,6,9,则这位选手五次射击环数的方差为_____.
样本容量
样本平均数
2
C
合作释疑
知识应用
B
当堂检测
必做题
新知应用
{3B4B98B0-60AC-42C2-AFA5-B58CD77FA1E5}甲
74
74
75
74
76
73
76
73
76
75
78
77
74
72
73
乙
75
73
79
72
76
71
73
72
78
74
77
78
80
71
75
例2: 某快餐公司的香辣鸡腿很受消费者的欢迎.现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿价格相同,品质相近.快餐公司决定通过检查鸡腿的重量来确定选购哪家的鸡腿.检查人员从两家的鸡腿中各抽取15个鸡腿,记录他们的质量(单位:g)如下:
根据表中数据,你认为快餐公司应该选购哪家加工厂的鸡腿?
解:
甲、乙两台编织机纺织一种毛衣,在5天中
两台编织机每天出的合格品数如下(单位:件):
甲:7 10 8 8 7 ;
乙:8 9 7 9 7 .
计算在这5天中,哪台编织机出合格品的波动较小?
所以是乙台编织机出的产品的波动性较小。
因为
当堂检测
选做题
A、甲 B、乙 C、一样 D、不能确定
B
即学即练
例2 在问题1 中,检查人员从两家的鸡腿中各随机
抽取15 个,记录它们的质量(单位:g)如下表所示.
根据表中的数据,你认为快餐公司应该选购哪家加工厂
的鸡腿?
解:样本数据的平均数分别是:
样本平均数相同,估计
这批鸡腿的平均质量相近.
甲
74
74
75
74
76
73
76
73
76
75
78
77
74
72
73
乙
75
73
79
72
76
71
73
72
78
74
77
78
80
71
75
课堂练习
小明和小亮在课外活动中,报名参加了短跑训练小组.在近几次百米训练中,所测成绩如图所示,请根据图中所示解答以下问题:
(1) 根据图中信息,补全下面的表格.
次数
1
2
3
4
5
小明
13.3
13.3
13.2
13.3
小亮
13.2
13.4
13.1
13.3
13.4
13.5
在解决实际问题时,方差的作用是什么?
反映数据的波动大小.
方差越大,数据的波动越大;方差越小,数据
的波动越小,可用样本方差估计总体方差.
知识归纳
课堂总结
1.方差:各数据与平均数的差的平方的平均数叫做这组数据的方差.
?????????=
?
2.方差意义:
方差越大,说明数据的波动越大; 方差越小,说明数据的波动越小.
可用样本方差估计总体方差.
而平均数、中位数、众数用来刻画数据的集中趋势.
同学们,再见
复习回顾
根据实际情况填写:(加权平均数、中位数、众数.)
①老板进货时关注卖出商品的 .
②评委给选手综合得分时关注
③被招聘的员工关注公司员工工资的
中位数
加权平均数
众数
新知探究
(1)甜玉米的产量可用什么量来描述?请计算后说明.
说明在试验田中,甲、乙两种甜玉米的平均产量相差不大.
可估计这个地区种植这两种甜玉米的平均产量相差不大.
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
了解方差的定义和计算公式;
会用方差的计算公式比较两组数
据的波动大小.
问题 农科院计划为某地选择合适的甜玉米种子.
选择种子时,甜玉米的产量和产量的稳定性是农科院所
关心的问题.为了解甲、乙两种甜玉米种子的相关情况,
农科院各用10 块自然条件相同的试验田进行试验,得到各试验田每公顷的产量(单位:t)如下表:
甲
7.65
7.50
7.62
7.59
7.65
7.64
7.50
7.40
7.41
7.41
乙
7.55
7.56
7.53
7.44
7.49
7.52
7.58
7.46
7.53
7.49
根据这些数据估计,农科院应该选择哪种甜玉米种
子呢?
目标导学一:方差及性质
2、方差的计算公式
=————————————————————
3、方差的意义
方差越大,___________越大;
方差越小,__________越小.
4.正如用样本的平均数估计总体的平均数一
样,也可以用样本的方差来估计________.
波动性
波动性
整体的方差
合作释疑
知识点一
各 数据与平均数的差的平方的平均数叫做这批数据的方差。公式为:
我们可以用“先平均,再求差,然后平方,最后再平均”得到的结果表示一组数据偏离平均值的情况。这个结果通常称为方差。
方差的定义及公式
新知归纳
1.方差的概念:
设有n个数据x1,x2,…,xn,各数据与它们的平均数 的差的平方分别是 ,我们用这些值的平均数,即
来衡量这组数据的波动大小,并把它叫作这组数据的方差.
解:甲、乙两团演员的身高平均数分别是
=___________________________
=_____
=____________________________
=_____
甲
乙
165
166
合作释疑
知识应用
例1:在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》, 参加表演的女演员的身高(单位:cm)
如表所示。
甲
163
164
164
165
165
166
166
167
乙
163
165
165
166
166
167
168
168
哪个芭蕾舞团女演员的身高更整齐?
精典例题
新知应用
例1: 在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团表演了舞剧《天鹅湖》,参加表演的女演员的身高(单位:cm)分别是:
{3B4B98B0-60AC-42C2-AFA5-B58CD77FA1E5}甲
163
164
164
165
165
166
166
167
乙
163
165
165
166
166
167
168
168
哪个芭蕾舞团女演员的身高更整齐?
1.数据-2,-1,0,1,2的方差是( )
A.0 B. C.2 D.4
2.在样本方差的计算式s2=10(1)[(x1-5)2+(x2-5)2+…+(x10-5)2]中,数字“10”表示__________,数字“5”表示___________.
3.在一次射击训练中,某位选手五次射击的环数分别为5,8,7,6,9,则这位选手五次射击环数的方差为_____.
样本容量
样本平均数
2
C
合作释疑
知识应用
B
当堂检测
必做题
新知应用
{3B4B98B0-60AC-42C2-AFA5-B58CD77FA1E5}甲
74
74
75
74
76
73
76
73
76
75
78
77
74
72
73
乙
75
73
79
72
76
71
73
72
78
74
77
78
80
71
75
例2: 某快餐公司的香辣鸡腿很受消费者的欢迎.现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿价格相同,品质相近.快餐公司决定通过检查鸡腿的重量来确定选购哪家的鸡腿.检查人员从两家的鸡腿中各抽取15个鸡腿,记录他们的质量(单位:g)如下:
根据表中数据,你认为快餐公司应该选购哪家加工厂的鸡腿?
解:
甲、乙两台编织机纺织一种毛衣,在5天中
两台编织机每天出的合格品数如下(单位:件):
甲:7 10 8 8 7 ;
乙:8 9 7 9 7 .
计算在这5天中,哪台编织机出合格品的波动较小?
所以是乙台编织机出的产品的波动性较小。
因为
当堂检测
选做题
A、甲 B、乙 C、一样 D、不能确定
B
即学即练
例2 在问题1 中,检查人员从两家的鸡腿中各随机
抽取15 个,记录它们的质量(单位:g)如下表所示.
根据表中的数据,你认为快餐公司应该选购哪家加工厂
的鸡腿?
解:样本数据的平均数分别是:
样本平均数相同,估计
这批鸡腿的平均质量相近.
甲
74
74
75
74
76
73
76
73
76
75
78
77
74
72
73
乙
75
73
79
72
76
71
73
72
78
74
77
78
80
71
75
课堂练习
小明和小亮在课外活动中,报名参加了短跑训练小组.在近几次百米训练中,所测成绩如图所示,请根据图中所示解答以下问题:
(1) 根据图中信息,补全下面的表格.
次数
1
2
3
4
5
小明
13.3
13.3
13.2
13.3
小亮
13.2
13.4
13.1
13.3
13.4
13.5
在解决实际问题时,方差的作用是什么?
反映数据的波动大小.
方差越大,数据的波动越大;方差越小,数据
的波动越小,可用样本方差估计总体方差.
知识归纳
课堂总结
1.方差:各数据与平均数的差的平方的平均数叫做这组数据的方差.
?????????=
?
2.方差意义:
方差越大,说明数据的波动越大; 方差越小,说明数据的波动越小.
可用样本方差估计总体方差.
而平均数、中位数、众数用来刻画数据的集中趋势.
同学们,再见
