18.1.2 平行四边形的判定 课件 2021-2022学年人教版八年级数学下册 (共21张PPT)
文档属性
| 名称 | 18.1.2 平行四边形的判定 课件 2021-2022学年人教版八年级数学下册 (共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 789.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-22 06:51:52 | ||
图片预览






文档简介
(共21张PPT)
18.1.2 平行四边形的判定
1
2
学习目标
掌握用一组对边平行且相等来判定平行四边形的方法。
会综合运用平行四边形的判定方法和性质来解决问题。
平行四边形的定义:
A
B
D
C
定义:两组对边分别平行的四边形叫做平行四边形
判定:
∵AB∥CD ,AD∥BC
∴四边形ABCD是平行四边形
平行四边形性质知识点回顾
两组对边分别平行的四边形叫做平行四边形。
A
B
D
C
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
概念:
几何描述:
平行四边形对边相等
平行四边形对角相等
性质:
平行四边形对角线互相平分
性质
定义
生活中的平行四边形
平行四边形
判定方法(4种)
温故知新
探索平行四边形的判定条件
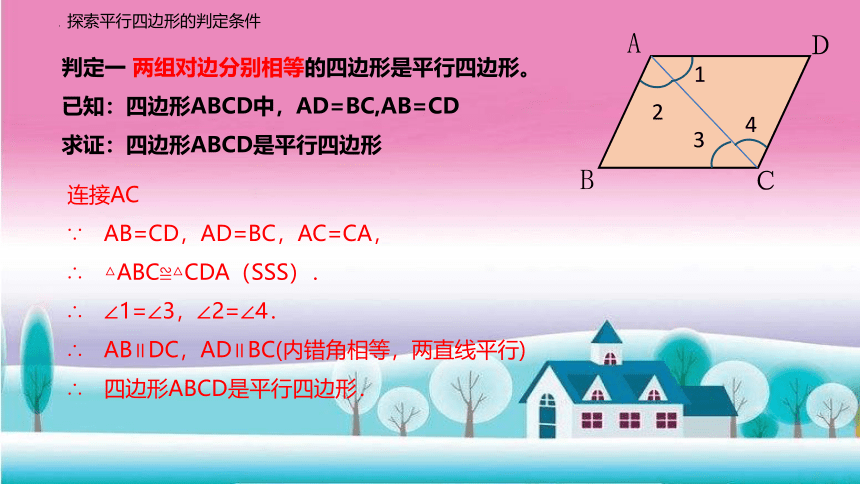
判定一 两组对边分别相等的四边形是平行四边形。
已知:四边形ABCD中,AD=BC,AB=CD
求证:四边形ABCD是平行四边形
A
B
D
C
1
2
3
4
连接AC
∵ AB=CD,AD=BC,AC=CA,
∴ △ABC≌△CDA(SSS).
∴ ∠1=∠3,∠2=∠4.
∴ AB∥DC,AD∥BC(内错角相等,两直线平行)
∴ 四边形ABCD是平行四边形.
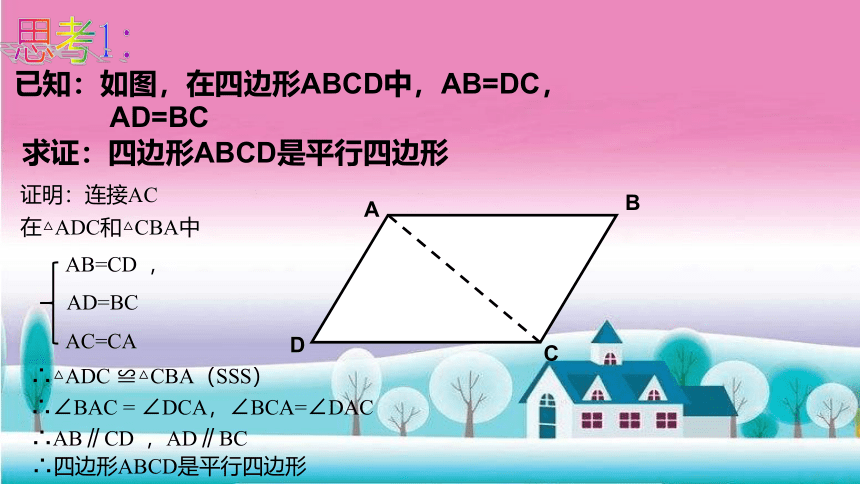
已知:如图,在四边形ABCD中,AB=DC,
AD=BC
求证:四边形ABCD是平行四边形
C
B
D
A
思考1:
证明:连接AC
∴四边形ABCD是平行四边形
在△ADC和△CBA中
AB=CD ,
AD=BC
AC=CA
∴△ADC ≌△CBA(SSS)
∴∠BAC = ∠DCA,∠BCA=∠DAC
∴AB∥CD ,AD∥BC
练一练(平行四边形的判定)
小王在钉制平行四边形框架时,采用了一种方法:
如图所示,将两根木条AC、BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形,
这种方法的依据是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
【详解】
解:由已知可得AO=CO,BO=DO,所以四边形ABCD是平行四边形,依据是对角线互相平分的四边形是平行四边形.故选:A.
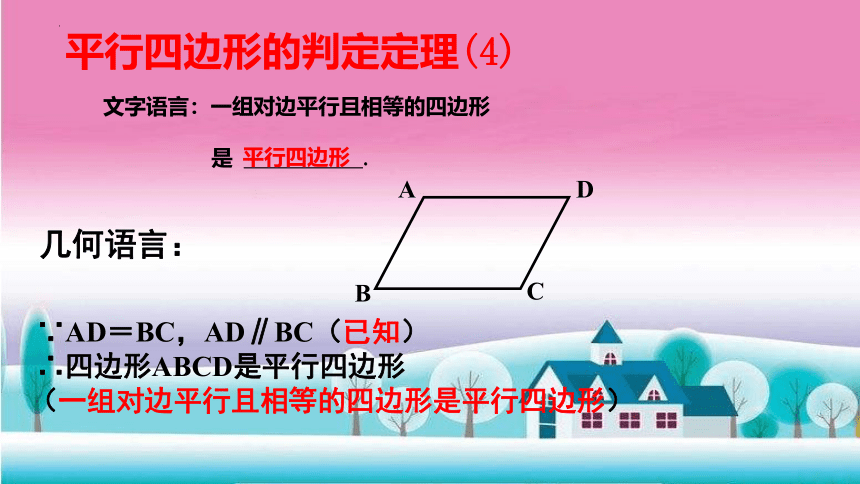
文字语言:一组对边平行且相等的四边形
是 .
平行四边形的判定定理(4)
平行四边形
几何语言:
∵AD=BC,AD∥BC(已知)
∴四边形ABCD是平行四边形
(一组对边平行且相等的四边形是平行四边形)
A
B
C
D
猜想:
A
B
D
C
两组对角分别相等的四边形是平行四边形.
与平行四边形判定有关的证明题
若这个四边形的一组对边相等,还需添加什么条件(并尝试证明) ,则这个四边形是平行四边形。
已知:四边形ABCD中,AD=BC, ____ _____
求证:四边形ABCD是平行四边形
连接AC ∵AD∥BC ∴∠1=∠3
∵ AD=BC,∠1=∠3,AC=CA,
∴ △ABC≌△CDA(SAS).
∴ ∠2=∠4.
∴ AB∥DC 而AD∥BC
∴ 四边形ABCD是平行四边形.
条件二:AD∥BC
A
B
D
C
1
2
3
4
已知:如图,AC∥ED,点B在AC上,且AB=ED=BC,
找出图中的平行四边形,并说明理由 .
强化训练
一组对边平行且相等的四边形是平行四边形
工人师傅在施工过程中不小心打破了一块平行四边形玻璃,刚好有两边是完好的,请同学们帮帮忙,有没有办法还原平行四边形?
A
B
C
小问题大学问
D
判定平行四边形的条件
下列选项中,不能判定四边形ABCD是平行四边形的是
A.∥CD, =CD B. ∥BC , ∥ CD
C.∥BC, =CD D. =CD ,∥BC
【详解】
A、由∥CD,=CD可以判断四边形ABCD是平行四边形;故本选项不符合题意;
B 、由∥BC,∥CD可以判断四边形ABCD是平行四边形;故本选项不符合题意;
C、∥BC, =CD不能判断四边形ABCD是平行四边形,有可能是等腰梯形;
故本选项符合题意;
D、由=CD,∥BC可以判断四边形ABCD是平行四边形;故本选项不符合题意,
故选C.
1、请你识别下列四边形哪些是平行四边形 为什么?
A
D
C
B
110°
70°
110°
⑴
⑷
⑶
A
B
C
D
120°
60°
5㎝
5㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
⑵
B
A
D
C
4.8㎝
4.8㎝
7.6㎝
7.6㎝
看谁最快
问题 平行四边形的判定有哪些?
B
O
D
A
C
5.一组对边平行且相等
1.定义:两组对边分别平行
2.两组对边分别相等
3.两组对角分别相等
4.对角线互相平分
与平行四边形判定有关的证明题
如图,在 ABCD中,E、F分别是AB,CD的中点.
求证:四边形DEBF是平行四边形.
【证明】
∵四边形ABCD是平行四边形
∴AB=CD,EB//FD
又∵EB= AB,FD= CD
∴EB=FD
∴四边形DEBF是平行四边形.
4、在下列条件中,不能判定四边形是平行四边形的是( )
AB∥CD, AD∥BC
AB=CD, AD=BC
(C)AB∥CD, AB=CD
(D) AB∥CD, ∠A=∠C
(E) AB∥CD, AD=BC
E
B
D
A
C
(两组对边分别平行)
(两组对边分别相等)
(一组对边平行且相等)
(两组对角分别相等)
A
B
D
C
等腰梯形
一组对边平行,另一组对边相等的四边形
不一定是平行四边形
问题2:如图,DE是△ABC的中位线,
DE与BC有怎样的关系?
D
E
两条线段的关系
位置关系
数量关系
分析:
DE与BC的关系
猜想:
DE∥BC
?
度量一下你手中的三角形,看看是否有同样的结论?并用文字表述这一结论.
课后回顾
平行四边形的判定方法
01
课后回顾
平行四边形判定证明
02
利用平行四边形的性质
和判定解决实际问题
03
同学们,再见
18.1.2 平行四边形的判定
1
2
学习目标
掌握用一组对边平行且相等来判定平行四边形的方法。
会综合运用平行四边形的判定方法和性质来解决问题。
平行四边形的定义:
A
B
D
C
定义:两组对边分别平行的四边形叫做平行四边形
判定:
∵AB∥CD ,AD∥BC
∴四边形ABCD是平行四边形
平行四边形性质知识点回顾
两组对边分别平行的四边形叫做平行四边形。
A
B
D
C
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
概念:
几何描述:
平行四边形对边相等
平行四边形对角相等
性质:
平行四边形对角线互相平分
性质
定义
生活中的平行四边形
平行四边形
判定方法(4种)
温故知新
探索平行四边形的判定条件
判定一 两组对边分别相等的四边形是平行四边形。
已知:四边形ABCD中,AD=BC,AB=CD
求证:四边形ABCD是平行四边形
A
B
D
C
1
2
3
4
连接AC
∵ AB=CD,AD=BC,AC=CA,
∴ △ABC≌△CDA(SSS).
∴ ∠1=∠3,∠2=∠4.
∴ AB∥DC,AD∥BC(内错角相等,两直线平行)
∴ 四边形ABCD是平行四边形.
已知:如图,在四边形ABCD中,AB=DC,
AD=BC
求证:四边形ABCD是平行四边形
C
B
D
A
思考1:
证明:连接AC
∴四边形ABCD是平行四边形
在△ADC和△CBA中
AB=CD ,
AD=BC
AC=CA
∴△ADC ≌△CBA(SSS)
∴∠BAC = ∠DCA,∠BCA=∠DAC
∴AB∥CD ,AD∥BC
练一练(平行四边形的判定)
小王在钉制平行四边形框架时,采用了一种方法:
如图所示,将两根木条AC、BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形,
这种方法的依据是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
【详解】
解:由已知可得AO=CO,BO=DO,所以四边形ABCD是平行四边形,依据是对角线互相平分的四边形是平行四边形.故选:A.
文字语言:一组对边平行且相等的四边形
是 .
平行四边形的判定定理(4)
平行四边形
几何语言:
∵AD=BC,AD∥BC(已知)
∴四边形ABCD是平行四边形
(一组对边平行且相等的四边形是平行四边形)
A
B
C
D
猜想:
A
B
D
C
两组对角分别相等的四边形是平行四边形.
与平行四边形判定有关的证明题
若这个四边形的一组对边相等,还需添加什么条件(并尝试证明) ,则这个四边形是平行四边形。
已知:四边形ABCD中,AD=BC, ____ _____
求证:四边形ABCD是平行四边形
连接AC ∵AD∥BC ∴∠1=∠3
∵ AD=BC,∠1=∠3,AC=CA,
∴ △ABC≌△CDA(SAS).
∴ ∠2=∠4.
∴ AB∥DC 而AD∥BC
∴ 四边形ABCD是平行四边形.
条件二:AD∥BC
A
B
D
C
1
2
3
4
已知:如图,AC∥ED,点B在AC上,且AB=ED=BC,
找出图中的平行四边形,并说明理由 .
强化训练
一组对边平行且相等的四边形是平行四边形
工人师傅在施工过程中不小心打破了一块平行四边形玻璃,刚好有两边是完好的,请同学们帮帮忙,有没有办法还原平行四边形?
A
B
C
小问题大学问
D
判定平行四边形的条件
下列选项中,不能判定四边形ABCD是平行四边形的是
A.∥CD, =CD B. ∥BC , ∥ CD
C.∥BC, =CD D. =CD ,∥BC
【详解】
A、由∥CD,=CD可以判断四边形ABCD是平行四边形;故本选项不符合题意;
B 、由∥BC,∥CD可以判断四边形ABCD是平行四边形;故本选项不符合题意;
C、∥BC, =CD不能判断四边形ABCD是平行四边形,有可能是等腰梯形;
故本选项符合题意;
D、由=CD,∥BC可以判断四边形ABCD是平行四边形;故本选项不符合题意,
故选C.
1、请你识别下列四边形哪些是平行四边形 为什么?
A
D
C
B
110°
70°
110°
⑴
⑷
⑶
A
B
C
D
120°
60°
5㎝
5㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
⑵
B
A
D
C
4.8㎝
4.8㎝
7.6㎝
7.6㎝
看谁最快
问题 平行四边形的判定有哪些?
B
O
D
A
C
5.一组对边平行且相等
1.定义:两组对边分别平行
2.两组对边分别相等
3.两组对角分别相等
4.对角线互相平分
与平行四边形判定有关的证明题
如图,在 ABCD中,E、F分别是AB,CD的中点.
求证:四边形DEBF是平行四边形.
【证明】
∵四边形ABCD是平行四边形
∴AB=CD,EB//FD
又∵EB= AB,FD= CD
∴EB=FD
∴四边形DEBF是平行四边形.
4、在下列条件中,不能判定四边形是平行四边形的是( )
AB∥CD, AD∥BC
AB=CD, AD=BC
(C)AB∥CD, AB=CD
(D) AB∥CD, ∠A=∠C
(E) AB∥CD, AD=BC
E
B
D
A
C
(两组对边分别平行)
(两组对边分别相等)
(一组对边平行且相等)
(两组对角分别相等)
A
B
D
C
等腰梯形
一组对边平行,另一组对边相等的四边形
不一定是平行四边形
问题2:如图,DE是△ABC的中位线,
DE与BC有怎样的关系?
D
E
两条线段的关系
位置关系
数量关系
分析:
DE与BC的关系
猜想:
DE∥BC
?
度量一下你手中的三角形,看看是否有同样的结论?并用文字表述这一结论.
课后回顾
平行四边形的判定方法
01
课后回顾
平行四边形判定证明
02
利用平行四边形的性质
和判定解决实际问题
03
同学们,再见
