18.2.1 矩形 课件 2021—2022学年人教版数学八年级下册(共18张PPT)
文档属性
| 名称 | 18.2.1 矩形 课件 2021—2022学年人教版数学八年级下册(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 592.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-22 05:35:11 | ||
图片预览





文档简介
(共18张PPT)
18.2.1 矩形
两组对边
分别平行
平行
四边形
四边形
平行四边形的性质有:
边: 对边平行且相等
角:对角相等;邻角互补
对角线:对角线互相平分
复习:
对称性:中心对称
观察思考:
矩形是平行四边形吗?
矩形和平行四边形有哪些异同?
我们从哪几个方面去研究矩形的性质?
边
角
对角线
周长
面积
对称性
对角线互相平分且相等
四个角都是直角
对边平行且相等
邻边之和 X 2
长 X 宽
轴对称,中心对称
矩形性质及特点
知识回顾
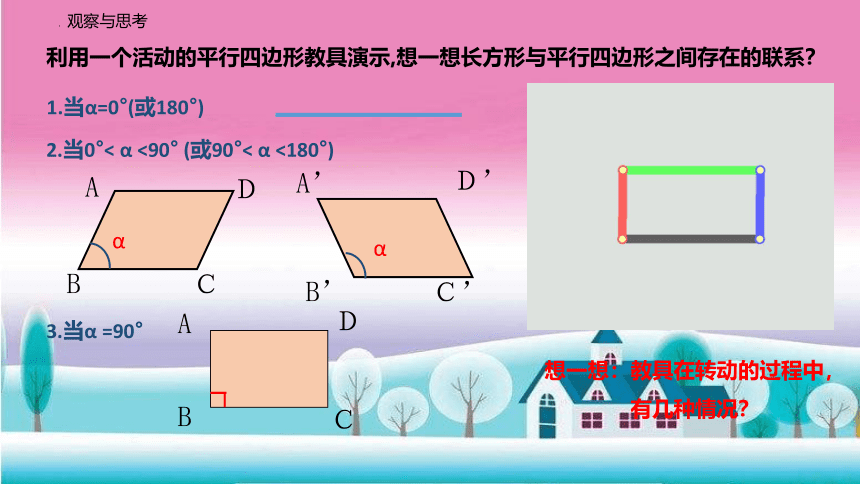
观察与思考
利用一个活动的平行四边形教具演示,想一想长方形与平行四边形之间存在的联系?
A
B
D
C
α
想一想:教具在转动的过程中,
有几种情况?
1.当α=0°(或180°)
2.当0°< α <90° (或90°< α <180°)
A’
B’
D’
C’
α
3.当α =90°
A
B
D
C
同样,我们能否通过研究矩形性质的逆命题,得到
判定矩形的方法呢?
探究猜想
矩形 性质
边 对边平行且相等
角 四个角都是直角
对角线 对角线互相平分且相等
请大家以前后座位为一组,分组讨论
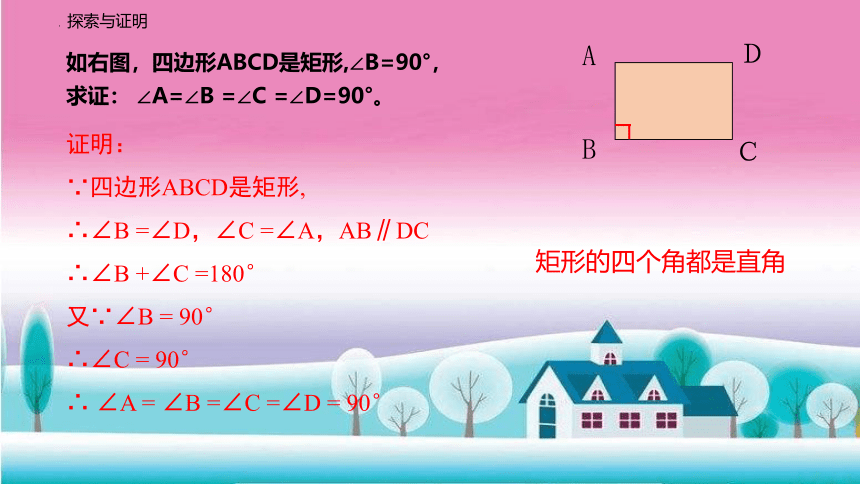
探索与证明
如右图,四边形ABCD是矩形,∠B=90°,
求证: ∠A=∠B =∠C =∠D=90°。
A
B
D
C
证明:
∵四边形ABCD是矩形,
∴∠B =∠D,∠C =∠A,AB∥DC
∴∠B +∠C =180°
又∵∠B = 90°
∴∠C = 90°
∴ ∠A = ∠B =∠C =∠D = 90°
矩形的四个角都是直角
我能行!
证明:矩形的对角线相等。
几何语言:在矩形ABCD中,
求证:AC=BD。
A
B
C
D
O
证明猜想
证明:
在
ABCD中
AB=DC,BD=CA,AD=DA
∴△BAD≌△CDA(SSS)
∴∠BAD=∠CDA
∵AB∥CD
∴∠BAD +∠CDA=180°
∴∠BAD=90°
∴四边形ABCD是矩形
(有一个内角是直角的平行四边形是矩形)
◆对角线相等的平行四边形是矩形吗?
四边形ABCD是平行四边形,AC=BD
四边形ABCD是矩形
已知:
求证:
利用矩形的性质求解
如图,矩形ABCD中,,,则AC的长是
A.4 B. C.8 D.10
【详解】
解:∵四边形ABCD是矩形,
∴OA=AC,OB=BD,AC=BD,∴OA=OB,
∵∠BOC=120°,∴∠AOB=60°,
∴△AOB是等边三角形,
∴OA=AB=3,∴AC=2OA=6,故选:B.
O
C
B
A
D
D
证明: 延长BO至D,使OD=BO,
连结AD、DC.
∵AO=OC, BO=OD
∴四边形ABCD是平行四边形.
∵∠ABC=900
∴ ABCD是矩形
∴AC=BD
1
2
1
2
∴BO= BD= AC
再探新知:
已知:在Rt△ABC中,∠ABC=90度,BO是AC上的中线. 求证: BO = AC
1
2
四边形
平行
四边形
一个角
是直角
矩形
对角线
相等
矩形
三个角
是直角
矩形
矩形
对角线互相
平分且相等
整理归纳
利用矩形的性质求解
如图,将长方形ABCD沿EF折叠,使顶点C恰好落在AB边的中点上.
若,,求BF的长.
【详解】
解:∵将长方形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上
∴BC’ = AB = 3,CF = C'F
在Rt△BC'F中,C’F2 = BF2+C'B2,
∴CF2 =(9-CF)2+9
∴CF = 5
∴BF = 4.
(2).矩形的两条对角线将矩形分成四个面积
相等的等腰三角形( )
(1).矩形是平行四边形( )
1.判断题
随堂练习:
例1 已知:如图,矩形ABCD的对角线AC、BD相交于点O,且E、F、G、H分别是AO、BO、CO、DO的中点,
求证:四边形EFGH是矩形
证明:
∵四边形ABCD是矩形
∴AC=BD(矩形的对角线相等)
AO=BO=CO=DO(矩形的对角线互相平分)
∵ E、F、G、H分别是AO、BO、CO、DO的中点
∴OE=OF=OG=OH
∴四边形EFGH是平行四边形(对角线互相平分的四边形是平行四边形)
∵EO+OG=FO+OH
即EG=FH
∴四边形EFGH是矩形(对角线相等的平行四边形是矩形)。
利用直角三角形斜边中线性质求解
三角形的两直角边长分别为6和8,则斜边上的中线长是( )
A.10 B.2.5 C.5 D.8
【详解】
已知直角三角形的两直角边为6、8,
则斜边长为=10,
故斜边的中线长为×10=5,
故选:C.
课堂小结
今天这堂课你有什么收获?
四边形
平行
四边形
一个角
是直角
矩形
对角线
相等
矩形
三个角
是直角
矩形
矩形
对角线互相
平分且相等
1、渗透了类比的学习方法
2、体会了图形判定探究的一般思路
证明
逆命题
(修正)
性质
猜想
判定定理
同学们,再见
18.2.1 矩形
两组对边
分别平行
平行
四边形
四边形
平行四边形的性质有:
边: 对边平行且相等
角:对角相等;邻角互补
对角线:对角线互相平分
复习:
对称性:中心对称
观察思考:
矩形是平行四边形吗?
矩形和平行四边形有哪些异同?
我们从哪几个方面去研究矩形的性质?
边
角
对角线
周长
面积
对称性
对角线互相平分且相等
四个角都是直角
对边平行且相等
邻边之和 X 2
长 X 宽
轴对称,中心对称
矩形性质及特点
知识回顾
观察与思考
利用一个活动的平行四边形教具演示,想一想长方形与平行四边形之间存在的联系?
A
B
D
C
α
想一想:教具在转动的过程中,
有几种情况?
1.当α=0°(或180°)
2.当0°< α <90° (或90°< α <180°)
A’
B’
D’
C’
α
3.当α =90°
A
B
D
C
同样,我们能否通过研究矩形性质的逆命题,得到
判定矩形的方法呢?
探究猜想
矩形 性质
边 对边平行且相等
角 四个角都是直角
对角线 对角线互相平分且相等
请大家以前后座位为一组,分组讨论
探索与证明
如右图,四边形ABCD是矩形,∠B=90°,
求证: ∠A=∠B =∠C =∠D=90°。
A
B
D
C
证明:
∵四边形ABCD是矩形,
∴∠B =∠D,∠C =∠A,AB∥DC
∴∠B +∠C =180°
又∵∠B = 90°
∴∠C = 90°
∴ ∠A = ∠B =∠C =∠D = 90°
矩形的四个角都是直角
我能行!
证明:矩形的对角线相等。
几何语言:在矩形ABCD中,
求证:AC=BD。
A
B
C
D
O
证明猜想
证明:
在
ABCD中
AB=DC,BD=CA,AD=DA
∴△BAD≌△CDA(SSS)
∴∠BAD=∠CDA
∵AB∥CD
∴∠BAD +∠CDA=180°
∴∠BAD=90°
∴四边形ABCD是矩形
(有一个内角是直角的平行四边形是矩形)
◆对角线相等的平行四边形是矩形吗?
四边形ABCD是平行四边形,AC=BD
四边形ABCD是矩形
已知:
求证:
利用矩形的性质求解
如图,矩形ABCD中,,,则AC的长是
A.4 B. C.8 D.10
【详解】
解:∵四边形ABCD是矩形,
∴OA=AC,OB=BD,AC=BD,∴OA=OB,
∵∠BOC=120°,∴∠AOB=60°,
∴△AOB是等边三角形,
∴OA=AB=3,∴AC=2OA=6,故选:B.
O
C
B
A
D
D
证明: 延长BO至D,使OD=BO,
连结AD、DC.
∵AO=OC, BO=OD
∴四边形ABCD是平行四边形.
∵∠ABC=900
∴ ABCD是矩形
∴AC=BD
1
2
1
2
∴BO= BD= AC
再探新知:
已知:在Rt△ABC中,∠ABC=90度,BO是AC上的中线. 求证: BO = AC
1
2
四边形
平行
四边形
一个角
是直角
矩形
对角线
相等
矩形
三个角
是直角
矩形
矩形
对角线互相
平分且相等
整理归纳
利用矩形的性质求解
如图,将长方形ABCD沿EF折叠,使顶点C恰好落在AB边的中点上.
若,,求BF的长.
【详解】
解:∵将长方形ABCD沿EF折叠,使顶点C恰好落在AB边的中点C′上
∴BC’ = AB = 3,CF = C'F
在Rt△BC'F中,C’F2 = BF2+C'B2,
∴CF2 =(9-CF)2+9
∴CF = 5
∴BF = 4.
(2).矩形的两条对角线将矩形分成四个面积
相等的等腰三角形( )
(1).矩形是平行四边形( )
1.判断题
随堂练习:
例1 已知:如图,矩形ABCD的对角线AC、BD相交于点O,且E、F、G、H分别是AO、BO、CO、DO的中点,
求证:四边形EFGH是矩形
证明:
∵四边形ABCD是矩形
∴AC=BD(矩形的对角线相等)
AO=BO=CO=DO(矩形的对角线互相平分)
∵ E、F、G、H分别是AO、BO、CO、DO的中点
∴OE=OF=OG=OH
∴四边形EFGH是平行四边形(对角线互相平分的四边形是平行四边形)
∵EO+OG=FO+OH
即EG=FH
∴四边形EFGH是矩形(对角线相等的平行四边形是矩形)。
利用直角三角形斜边中线性质求解
三角形的两直角边长分别为6和8,则斜边上的中线长是( )
A.10 B.2.5 C.5 D.8
【详解】
已知直角三角形的两直角边为6、8,
则斜边长为=10,
故斜边的中线长为×10=5,
故选:C.
课堂小结
今天这堂课你有什么收获?
四边形
平行
四边形
一个角
是直角
矩形
对角线
相等
矩形
三个角
是直角
矩形
矩形
对角线互相
平分且相等
1、渗透了类比的学习方法
2、体会了图形判定探究的一般思路
证明
逆命题
(修正)
性质
猜想
判定定理
同学们,再见
