2021-2022学年人教版数学八年级下册 第十六章二次根式 复习与测试课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册 第十六章二次根式 复习与测试课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 691.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-22 07:12:32 | ||
图片预览






文档简介
(共17张PPT)
16 复习与测试
知识点盘点
定义
形如 (a≥0)的式子叫作二次根式
“ ”称为二次根式
性质
(a≥0)是一个非负数,即 ≥0
=|a|即a≥0,等于a;a<0,等于-a
( )2=a (a≥0)
最简二次根式
1.被开方数不含分母
2.被开方数不含开方开得尽的因数或因式
同类二次根式
几个二次根式化简成二次根式后被开方数相同,这几个二次根式就是同类二次根式
运算法则
一化二找三合并
考点一 二次根式的相关概念有意义的条件
例1 当x是怎样的实数时,下列各式在实数范围内有意义?
解:(1)∵无论x为何实数,
∴当x=1时, 在实数范围内有意义.
(2)∵无论x为何实数,-x2-2x-3=-(x+1)2-2<0,
∴无论x为何实数, 在实数范围内都无意义.
练
练
一
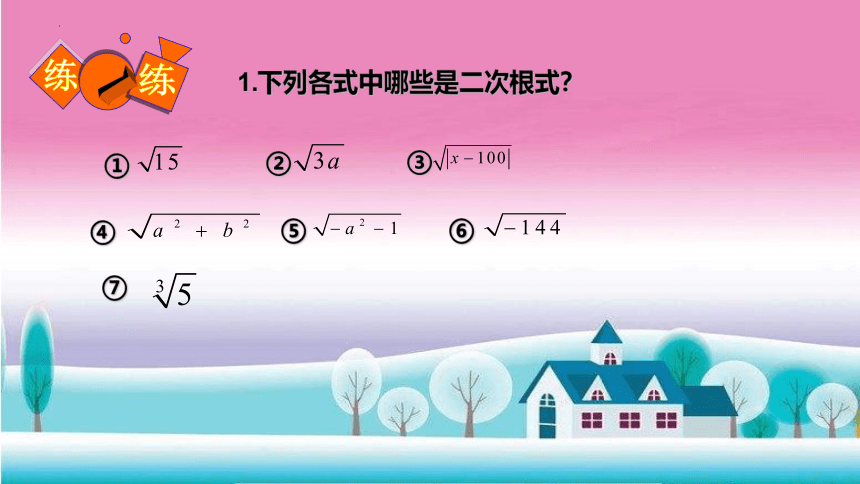
1.下列各式中哪些是二次根式?
①
②
③
⑥
⑤
④
⑦
考点三 二次根式的运算及应用
例3 计算:
解:
开得尽方
分母
最简二次根式
满足下列两个条件的二次根式,叫做最简二次根式.
(1)被开方数不含_______;
(2)被开方数中不含能___________的因数或因式.
3.
方法总结
典例解析:
例2: 的结果是________.
【分析】
由分式性质可知:x≠0,根据二次根式的性质可得:当x>0时, ;当时x<0时, ,分别代入原式化简即可.
【详解】
由分式性质可知:x≠0,
当x>0时,
当x<0时, ;
故答案为:0或2.
0或2
典例解析:
变式3:(1)若 ,求x+y的值.
(2)求使 有意义的的取值范围.
【详解】
解:(1)∵|x-3|+(y+3)2=0,
∴|x-3|=0,(y+3)2=0,
即x-3=0,y+3=0
解得:x=3,y=-3
∴x+y=0
(2)要使 有意义,需使a≥0,-a≥0∴a=0
所以使 有意义的取值范围是a=0
例5 在一个边长为 cm的正方形内部,挖去一个边长为 cm的正方形,求剩余部分的面积.
解:由题意得
即剩余部分的面积是
知识点二 二次根式的性质
例2.若实数a,b满足 则 .
1
典例解析:
【详解】
(1)∵
∴m=2,n=4,
∴2m+3n=16
∴16的平方根为±4;
2. 计算:
解:
1.下列运算正确的是( )
C
2. 若等腰三角形底边长为 ,底边的高为
则三角形的面积为 .
练
练
一
计算:
解:
知识点 二次根式的化简求值
例4 先化简,再求值: ,其中
.
解:
当 时,
原式
小结
同学们,再见
16 复习与测试
知识点盘点
定义
形如 (a≥0)的式子叫作二次根式
“ ”称为二次根式
性质
(a≥0)是一个非负数,即 ≥0
=|a|即a≥0,等于a;a<0,等于-a
( )2=a (a≥0)
最简二次根式
1.被开方数不含分母
2.被开方数不含开方开得尽的因数或因式
同类二次根式
几个二次根式化简成二次根式后被开方数相同,这几个二次根式就是同类二次根式
运算法则
一化二找三合并
考点一 二次根式的相关概念有意义的条件
例1 当x是怎样的实数时,下列各式在实数范围内有意义?
解:(1)∵无论x为何实数,
∴当x=1时, 在实数范围内有意义.
(2)∵无论x为何实数,-x2-2x-3=-(x+1)2-2<0,
∴无论x为何实数, 在实数范围内都无意义.
练
练
一
1.下列各式中哪些是二次根式?
①
②
③
⑥
⑤
④
⑦
考点三 二次根式的运算及应用
例3 计算:
解:
开得尽方
分母
最简二次根式
满足下列两个条件的二次根式,叫做最简二次根式.
(1)被开方数不含_______;
(2)被开方数中不含能___________的因数或因式.
3.
方法总结
典例解析:
例2: 的结果是________.
【分析】
由分式性质可知:x≠0,根据二次根式的性质可得:当x>0时, ;当时x<0时, ,分别代入原式化简即可.
【详解】
由分式性质可知:x≠0,
当x>0时,
当x<0时, ;
故答案为:0或2.
0或2
典例解析:
变式3:(1)若 ,求x+y的值.
(2)求使 有意义的的取值范围.
【详解】
解:(1)∵|x-3|+(y+3)2=0,
∴|x-3|=0,(y+3)2=0,
即x-3=0,y+3=0
解得:x=3,y=-3
∴x+y=0
(2)要使 有意义,需使a≥0,-a≥0∴a=0
所以使 有意义的取值范围是a=0
例5 在一个边长为 cm的正方形内部,挖去一个边长为 cm的正方形,求剩余部分的面积.
解:由题意得
即剩余部分的面积是
知识点二 二次根式的性质
例2.若实数a,b满足 则 .
1
典例解析:
【详解】
(1)∵
∴m=2,n=4,
∴2m+3n=16
∴16的平方根为±4;
2. 计算:
解:
1.下列运算正确的是( )
C
2. 若等腰三角形底边长为 ,底边的高为
则三角形的面积为 .
练
练
一
计算:
解:
知识点 二次根式的化简求值
例4 先化简,再求值: ,其中
.
解:
当 时,
原式
小结
同学们,再见
