2021-2022学年人教版数学七年级下册 第六章实数 复习与测试课件(共19张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学七年级下册 第六章实数 复习与测试课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 477.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-22 07:26:38 | ||
图片预览




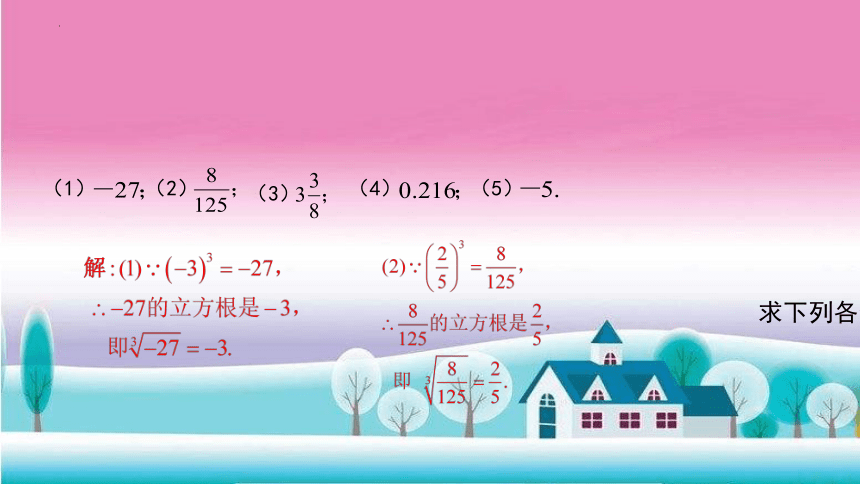

文档简介
(共19张PPT)
6 复习与测试
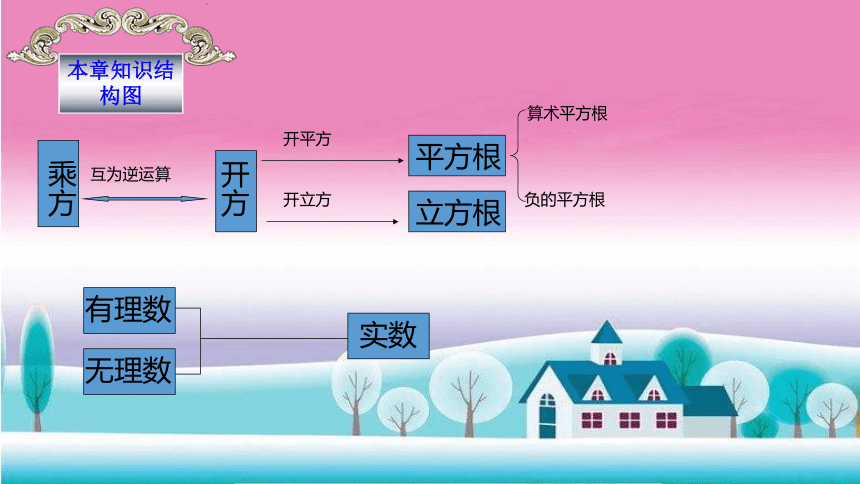
本章知识结构图
乘方
开方
开平方
开立方
平方根
立方根
有理数
无理数
实数
互为逆运算
算术平方根
负的平方根
立方根的定义:
一般地,如果一个数的立方等于a,那么这个数就叫做a的立方根,也叫做a的三次方根.记作 .
其中a是被开方数,3是根指数,符号“ ”读做“三次根号”.
3
5.立方根的性质:
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零。
专题一 开方运算
1)9的算术平方根是______;
3
2
2) 的算术平方根是______;
例1: 填空:
追踪练习:
1、估算 -2的值 ( )
A.在1和2之间 B.在2和3之间
C.在3和4之间 D.在4和5之间
B
(1)
(2)
(3)
(4)
(5)
求下列各数的立方根:
课后练习题
1.求下列各数的算术平方根:
(1) 0.04;(2) 1; (3) 56 ; (4) (-3)2 ; (5)
49
64
3.求下列各数的立方根:
(1) 121;(2) 16; (3) 0 ; (4) (-3)2 ; (5)
9
4
2.求下列各数的平方根:
(1) -0.008;(2) 43; (3) -64; (4) (-3)3; (5)
27
8
4.求下列各式的值:
求根也好,求值也好,关键要弄清它是什么意思,然后可以选择定义和性质来求.
小试牛刀
1.判断:
(1) ( )
(2) 的绝对值是 ; ( )
(3) 的相反数是 . ( )
×
×
1、 在数轴上表示下列各点,比较它们的大小,
并用“<”连接它们.
-2 -1 0 1 2 3
1
-2
-2< < 1< <
2、 估计 位于( )
A.0~1之间 B.1~2之间 C.2~3之间 D.3~4之间
B
追踪训练
= 2
=2
利用定义
无理数也有乘除运算,在后面的章节里将会学习,也满足先定符号,再计算.
实数的运算
例: 比较下列各组数的大小:
解 : (1)因为 12 < 42,
所以 < 4,
所以 -1< 3;
(2)因为 10 > 32 ,
所以
所以
若 ,
求 的值.
利用平方根(或立方根)的概念解下列方程:
(1)9(x-3)2=64;
(2)(2x-1)3=-8.
1、无限不循环的小数 叫做无理数.
有理数和无理数统称实数.
4、在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样
6、在进行实数的运算时,有理数的运算法则及运算性质同样适用。
实数的有关概念和性质
2、实数与数轴上的点是一一对应的.
3、同样的,平面直角坐标系中的点与有序实数对是一一对应的.
5、实数的大小比较方法有:利用数轴比较、利用绝对值比较、求平方比较、求差比较、求商比较和计算近似值比较等方法。
解下列关于的方程:
(1)
(2)
解下列关于 x 的方程:
(1)
(2)
有理数集合:{ };
把下列各数填在相应的大括号内:
整数集合:{ ……};
奇数集合:{ ……};
无理数集合:{ }。
-1,0,
-1
-1,,3.14,0,3.3·3·,,
π, 2.1010010001…
要学会计算哟!
1·计算:
2、(结果保留3个有效数字)
注意:计算过程中要多保留一位!
同学们,再见
6 复习与测试
本章知识结构图
乘方
开方
开平方
开立方
平方根
立方根
有理数
无理数
实数
互为逆运算
算术平方根
负的平方根
立方根的定义:
一般地,如果一个数的立方等于a,那么这个数就叫做a的立方根,也叫做a的三次方根.记作 .
其中a是被开方数,3是根指数,符号“ ”读做“三次根号”.
3
5.立方根的性质:
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零。
专题一 开方运算
1)9的算术平方根是______;
3
2
2) 的算术平方根是______;
例1: 填空:
追踪练习:
1、估算 -2的值 ( )
A.在1和2之间 B.在2和3之间
C.在3和4之间 D.在4和5之间
B
(1)
(2)
(3)
(4)
(5)
求下列各数的立方根:
课后练习题
1.求下列各数的算术平方根:
(1) 0.04;(2) 1; (3) 56 ; (4) (-3)2 ; (5)
49
64
3.求下列各数的立方根:
(1) 121;(2) 16; (3) 0 ; (4) (-3)2 ; (5)
9
4
2.求下列各数的平方根:
(1) -0.008;(2) 43; (3) -64; (4) (-3)3; (5)
27
8
4.求下列各式的值:
求根也好,求值也好,关键要弄清它是什么意思,然后可以选择定义和性质来求.
小试牛刀
1.判断:
(1) ( )
(2) 的绝对值是 ; ( )
(3) 的相反数是 . ( )
×
×
1、 在数轴上表示下列各点,比较它们的大小,
并用“<”连接它们.
-2 -1 0 1 2 3
1
-2
-2< < 1< <
2、 估计 位于( )
A.0~1之间 B.1~2之间 C.2~3之间 D.3~4之间
B
追踪训练
= 2
=2
利用定义
无理数也有乘除运算,在后面的章节里将会学习,也满足先定符号,再计算.
实数的运算
例: 比较下列各组数的大小:
解 : (1)因为 12 < 42,
所以 < 4,
所以 -1< 3;
(2)因为 10 > 32 ,
所以
所以
若 ,
求 的值.
利用平方根(或立方根)的概念解下列方程:
(1)9(x-3)2=64;
(2)(2x-1)3=-8.
1、无限不循环的小数 叫做无理数.
有理数和无理数统称实数.
4、在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样
6、在进行实数的运算时,有理数的运算法则及运算性质同样适用。
实数的有关概念和性质
2、实数与数轴上的点是一一对应的.
3、同样的,平面直角坐标系中的点与有序实数对是一一对应的.
5、实数的大小比较方法有:利用数轴比较、利用绝对值比较、求平方比较、求差比较、求商比较和计算近似值比较等方法。
解下列关于的方程:
(1)
(2)
解下列关于 x 的方程:
(1)
(2)
有理数集合:{ };
把下列各数填在相应的大括号内:
整数集合:{ ……};
奇数集合:{ ……};
无理数集合:{ }。
-1,0,
-1
-1,,3.14,0,3.3·3·,,
π, 2.1010010001…
要学会计算哟!
1·计算:
2、(结果保留3个有效数字)
注意:计算过程中要多保留一位!
同学们,再见
